Производные высших порядков.

Суть: производная второго порядка – производная от производной первого порядка, производная третьего порядка – производная от производной второго и т.д. Физический смысл – изменение изменения скорости, т.е. ускорение.

Производная f’(x) является функцией того же аргумента х, что и исходная функция. Поэтому ее можно опять дифференцировать, т.е. вычислять предел:

lim_∆x->0 (f’(x+∆x)-f’(x))/∆x

Если этот предел существует и конечен, то он называется второй производной от функции f(x) в точке х.

(f’(x))’=d²f(x)/dx²

F⁽ⁿ⁾(x)=(f^(n-1) (x))’

29. Функция многих переменных. Частные производные.

Суть: напр., ф-ция двух переменных - каждой паре переменных по некоторому закону ставится в соответствие одно значение функции. На графиках такие функции отображают в 3D пространстве. Переменных может быть и больше. Частную производную находят по каждой из переменных отдельно, для этого одну из переменных используют для дифференцирования, а вторую просто не трогают.

Если каждому упорядоченному набору возможных значений аргументов x₁, x₂, … x_n по закону f поставлено в соответствие единственное число, то говорят, что задана функция n переменных: y = f(x₁, x₂, … x_n). Для задания такой функции необходимо, кроме того, указать n-мерную область D возможных значений независимых переменных (при n=2 D – часть плоскости).

Пусть f(x,y) – функция двух переменных.

Зафиксируем y (y=y₀). Тогда f(x,y₀) – функция переменной x.

Производная от этой функции: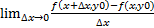

Если этот предел существует и конечен, то его значение – частная производная по x при y=y0.

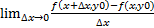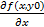= = f’_x (x,y₀)

Частная производная от f(x0,y) по y:

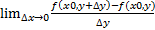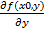= = f’_x (x₀,y)

Производные второго порядка:

Вторая производная по x:

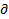²f(x,y) / 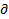x² = f”_xx (x,y)

Вторая производная по y:

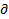²f(x,y) / 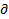y² = f”_yy (x,y)

Вторая смешанная производная по x и y (по y и x):

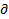²f(x,y) / 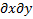= f”_xy (x,y) = 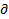²f(x,y) / 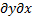= f”_yx (x,y)

30. Формула Тейлора.

В учебнике вместо a – x₀.

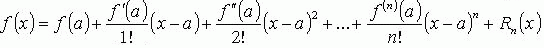
R_n(x) = f⁽ⁿ⁺¹⁾(c) / (n+1)! × (x-a)ⁿ⁺¹ - остаточный член в форме Лагранжа

Частный случай – формула Маклорена (при a=0):

f(x) = f(0) + f’(0)x + f”(0) / 2! × X² + … + f⁽ⁿ⁾(0) / n! × xⁿ + f⁽ⁿ⁺¹⁾(c) / (n+1)! × xⁿ⁺¹ (0<c<x)

31. Первообразные и неопределенные интегралы.

Интегрирование – обратная дифференцированию функция – отыскание функции по ее производной.

Функция F(x), производная которой равна некоторой функции f(x) – первообразная для f(x).

F’(x) = f(x)

Производная постоянной равна 0. Исходя из этого, первообразные для одной и той же функции отличаются на постоянную величину.

Все первообразные f(x): F(x) + C.

Множество всех первообразных для функции f(x) – неопределенный интеграл от этой функции:

∫f(x)dx = F(x) + C.

Основные свойства неопределенного интеграла.

а) константу можно вынести за интеграл:

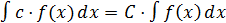
б) интеграл суммы равен сумме интегралов:

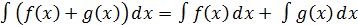
Способы вычисления неопределенного интеграла.

1) интегрирование по частям

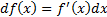
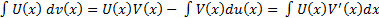
Более понятный вариант:

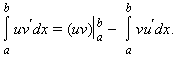
Пример:

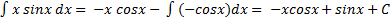
2) метод замены

Замена переменной интегрирования x на некоторую функцию φ(t), чтобы преобразовать исходный интеграл к более простому виду.

Пример:

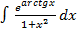
Замена:

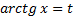
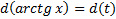
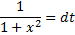
Тогда

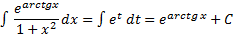
Интеграл Римана.

Интеграл Римана = определенный интеграл.

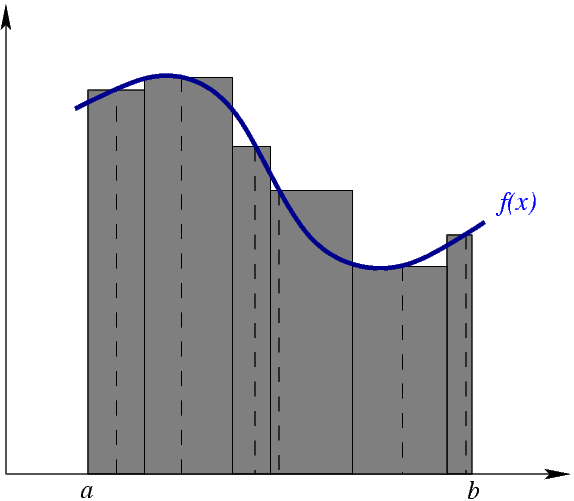
Из википедии: «Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке.»

Вообще определенный интеграл – это площадь криволинейной трапеции.

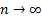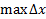Из учебника: «Если независимо от способа разбиения отрезка [a,b] на части, для функции f(x) существует конечный предел интегральной суммы при и _i 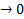, то этот предел называется определенным интегралом f(x) от a до b, а сама функция f(x) – интегрируемой на отрезке [a,b].»

Обозначается так:

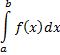
a, b – нижний и верхний пределы интеграла.

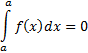
Интеграл существует для всех непрерывных функций.