Производные высших порядков

Первая производная функции 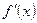сама является функцией, которая также может иметь производную.

Определение

Производной n–го порядка называется производная от производной (n–1)–го порядка.

Обозначение производных: 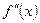– второго порядка (или вторая производная), 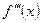– третьего порядка (или третья производная).

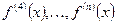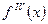Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры, например, или и т.д.

5.6. Основные теоремы дифференциального исчисления – теоремы Ферма, Ролля, Лагранжа

Теорема

Ферма. Пусть функция 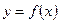определена на интервале 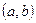и имеет наибольшее (наименьшее) значение в точке 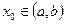. Тогда, если в точке 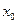существует производная этой функции, то она равна нулю, т.е. .

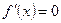Геометрический смысл теоремы Ферма: если в точке 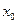дифференцируемая функция принимает наибольшее (наименьшее) значение, то в точке 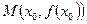касательная к графику этой функции параллельна оси 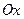(Рис. 5.6.1).

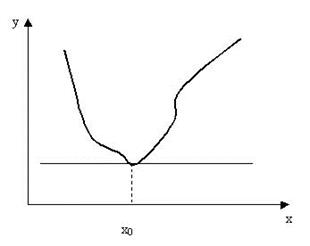
Рис. 5.6.1

Заметим, что Теорема неверна, если функция рассматривается на отрезке 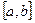: в этом случае она может принимать наибольшее и ли наименьшее значение на концах отрезка, где производная не равна нулю.

Теорема (Ролля)

Пусть функция 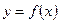непрерывна на отрезке 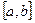и дифференцируема на интервале 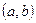, причем 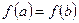. Тогда существует точка 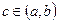, в которой .

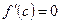Геометрический смысл теоремы Ролля: если функция, непрерывная на отрезке и дифференцируемая внутри ее, на концах этого отрезка принимает одинаковые значения, то хотя бы в одной внутренней точке этого отрезка касательная к графику функции параллельна оси 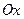(Рис. 5.6.2).

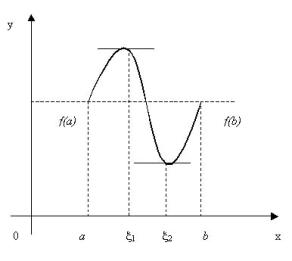
Рис. 5.6.2

Теорема (Лагранжа)

Пусть функция 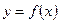непрерывна на отрезке 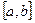и дифференцируема на интервале 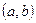. Тогда существует такая точка 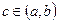, что справедлива формула

.

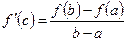(5.6.1)

Теорема Лагранжа имеет геометрический смысл (рис. 5.6.3). Секущая, проходящая через точк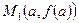и и 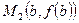, имеет угловой коэффициент, равный 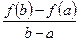, а 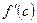– угловой коэффициент касательной к графику функции в точке 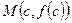. Теорема Лагранжа утверждает, что существует хотя бы одна точка интервала 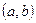, где касательная к графику функции параллельна секущей 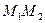. Приведенные теоремы позволяют сформулировать и обосновать теоремы Лопиталя для раскрытия неопределенностей.

Правило Лопиталя

Определение

Будем говорить, что отношение двух функци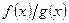й при 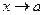есть неопределенность вида 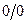, если .

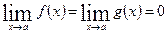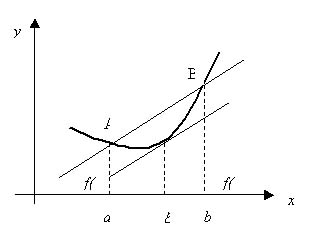
Рис. 5.6.3

Раскрыть эту неопределенность означает вычислить предел 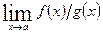, если он существует.

Теорема (Лопиталя)

Пусть функци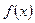и и 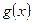определены и дифференцируемы в некоторой окрестности точки 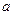, за исключением, быть может, самой точки 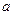. Кроме того, пусть также 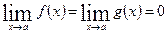, причем 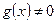в указанной окрестности точки 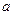. Тогда если существует предел отношения Ошибка! Объект не может быть создан из кодов полей редактирования. (конечный или бесконечный), существует и предел 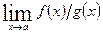, причем справедлива формула:

.

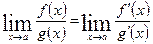(5.7.1)

Эту теорему обычно называют правилом Лопиталя.

Замечание 1

Правило Лопиталя можно применить повторно, есл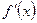и и 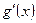удовлетворяют тем же требованиям, что и исходные функци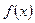и и .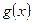

Замечание 2

Теорема остается верной и в случае, когда ( ).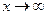

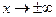Пример

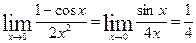
Здесь мы дважды последовательно применили правило Лопиталя, поскольку два раза имели дело с неопределенностью вида .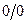

Неопределенность вида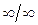

Определение

Будем называть отношение двух функци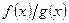й при 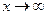неопределенностью вида 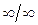, ес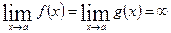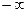ли , или 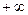. В этом случае правило Лопиталя остается справедливым при замене условия 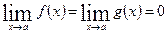на условие .

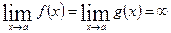Пример

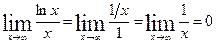
Другие виды неопределенностей

Неопределенности вида 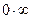и 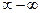можно свести к неопределенностям вида 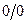и 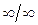с помощью несложных алгебраических преобразований.

Пример

Найти предел .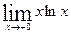

Решение

Здесь имеем неопределенность вида 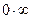. Преобразуем функцию под знаком предела: 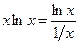, в результате имеем неопределенность вида 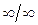при 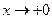. Теперь, применяя правило Лопиталя, получаем .

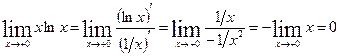Неопределенности вида 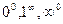, имеющие место при рассмотрении пределов функций 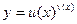, сводятся к неопределенностям вида 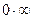с помощью тождественного преобразования

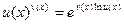
Пример

Найти предел .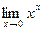

Решение

Это неопределенность вида 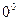; используя предыдущую формулу, имеем с учетом только что решенного примера .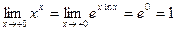