Производные основных элементарных функций, производные высших порядков.

Производная основных элементарных ф-ий: ; ; ;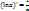

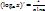Производная высших порядков: y=f(x), тогда y’=f’(x), y’’=f’’(x), y’’’=f’’’(x), =( )’

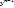28. Основные теоремы дифференциального исчисления.

Теорема Ферма.

ф-я 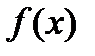определена на 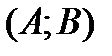и в нек-рой точке 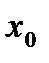этого интервала имеет наиб. или наим. значение, тогда если в этой точке определена производная, то она =0, т.е.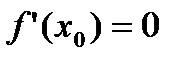

Пр. 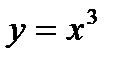в точке 0 производная =0.

Теорема Ролля.

Пусть на отрезке 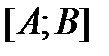определена ф-я 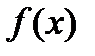, причем: 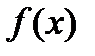непрерывна на 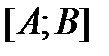, 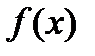дифференцируема на ,

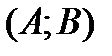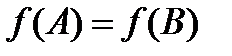
Тогда сущ-ет точка 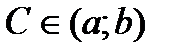, что

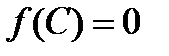
Теорема Лагранжа.

Пусть на 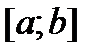определена ф-я 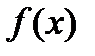причем:

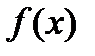непрерывна на 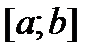, 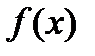диффер. на 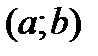Тогда сущ-ет точка С, принадлежащ. 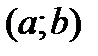, такая, что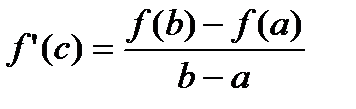

Теорема Коши.

Пусть 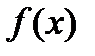и 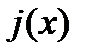непрерывны на 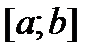и дифференцируемы на 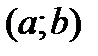и пусть кроме того 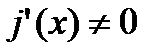, тогда сущ-ет 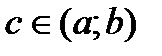такая, что 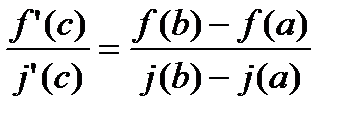. Если в кач-ве 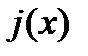взять ф-ю. 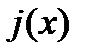= 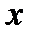, то получим т. Лагранжа. Если т. Лагранжа положить 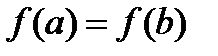, то получим т. Коши.

Теорема Лапиталля-Бернулли.

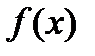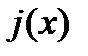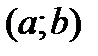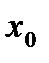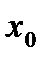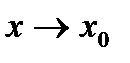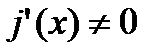Пусть и определены и дифф. на содержащим точку за исключением быть может самой точки . Пусть предел при и на 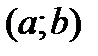, тогда если сущ-ет конечный предел, при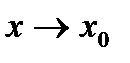 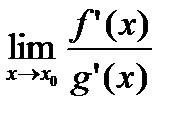то сущ-ет и 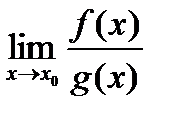причем они равны.

29. Правило Лопиталя.

К разряду неопределенностей принято относить следующие соотношения:

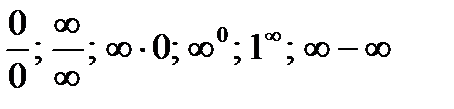
Т.(правило Лопиталя).Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

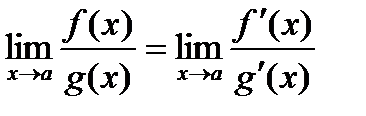
Доказ-во.Применив формулу Коши, получим: 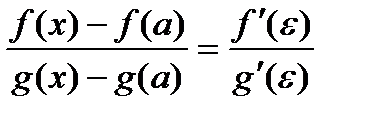, где e - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0: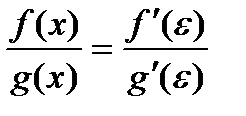

Пусть при х®а отношение 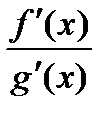стремится к некоторому пределу. Т.к. точка e лежит между точками а и х, то при х®а получим e®а, а следовательно и отношение 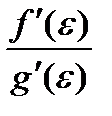стремится к тому же пределу. Таким образом, можно записать: .

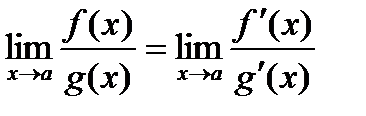Пример:Найти предел .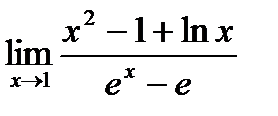

при вычислении предела получается неопределенность вида 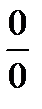. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.

f¢(x) = 2x + 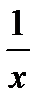; g¢(x) = e^x;

;

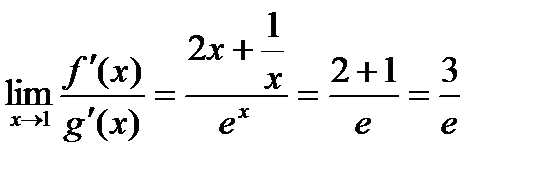30. Возрастание и убывание функций.

Т.1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f¢(x) ³ 0.

2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f¢(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

Если функция f(x) убывает на отрезке [a, b], то f¢(x)£0 на этом отрезке. Если f¢(x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b].

Данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).

Точки экстремума.

Функция f(x) имеет в точке х₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х₁. Функция f(x) имеет в точке х₂ минимум, если f(x₂ +Dx) > f(x₂) при любом Dх (Dх может быть и отрицательным).Точки максимума и минимума функции называются точками экстремума.

Т.(необход.ус-е сущ-я экстремума) Если функция f(x) дифференцируема в точке х = х₁ и точка х₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. функция у = х³, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.

Критическими точками функции наз-ся точки, в кот.производная ф-ии не сущ-т или =0.

Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.

функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.

Т. (Достаточные условия существования экстремума)

Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х₁, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х₁).

Если при переходе через точку х₁ слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х₁ функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.