Задачи для самостоятельного решения. В задачах 1-7 решить системы уравнений:
В задачах 1-7 решить системы уравнений:
1. 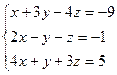 . 2.
. 2. 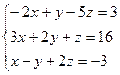 .
.
3. 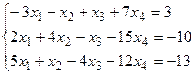 .4.
.4. 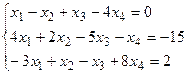 .
.
5. 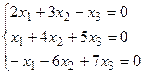 . 6.
. 6. 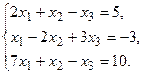
7. 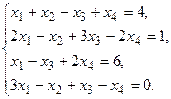
8.Найти сумму матриц
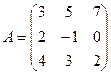 ,
, 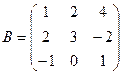 .
.
9. Найти матрицу 2А+5В, если
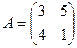 ,
, 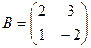 .
.
10..Найти значение матричного многочлена 2А2+3А+5Е при 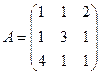 , если Е –единичная матрица третьего порядка.
, если Е –единичная матрица третьего порядка.
11.Найти матрицу АВ, если 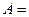
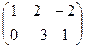 , В=
, В= 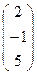 .
.
12. Дана матрица 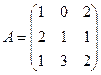 . Найти матрицу
. Найти матрицу 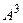 .
.
Ответы: 1.(1;-2;1). 2.(3;4;-1). 3.( 1+t; -2+3t; 4-t; t ).
4. ( -1+2t; 2-t; 3+t; t ). 5.( 0; 0; 0 ). 6.( 1 ;5 ;2 ). 7.( 1; 2; 3; 4 ).8. 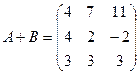 . 9.
. 9. 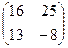
10. 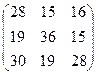 . 11. АВ=
. 11. АВ= 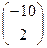 . 12.
. 12. 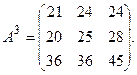
Занятие 3. Ранг матрицы. Вычисление обратной матрицы. Решение систем уравнений с помощью обратной матрицы
Вычисление ранга матрицы
Пусть дана матрица, содержащая m строк и n столбцов
А= 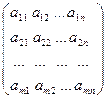 .
.
Выделим в ней произвольным образом k строк и k столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка; определитель этой матрицы называется миноромk-го порядка матрицы А. Очевидно, что в общем случае таких миноров k-го порядка может быть несколько. При этом максимальный порядок миноров равен минимальному из чисел m и n, т. е.
max k = min(m,n)
Из всех возможных миноров матрицы А выделим те из них, которые отличны от нуля. В свою очередь, среди этих миноров можно найти, по крайней мере, один минор наибольшего порядка.
Наибольший порядок миноров, отличных от нуля, называется рангом матрицы .
Для вычисления ранга матрицы приведем ее к ступенчатому виду: Будем изменять матрицу А размера m´n так, чтобы сохранялся ее ранг. В результате матрица приводится к виду:
 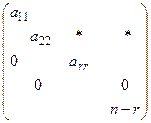 ; ; 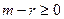 , , 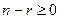 . (3.1) . (3.1) | |
| m-r{ |
Матрица (3.1) имеет ступенчатый вид, где 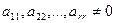 , * - некоторые числа.
, * - некоторые числа.
Ранг этой матрицы = r.
Ранг матрицы не меняют следующие операции:
1. Прибавление к одной строке другой строки, умноженной на число;
2. Перемену местами строк, столбцов.
Рассмотрим элемент 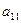 . Пусть
. Пусть 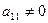 , тогда умножая первую строку на подходящие числа (для 2-ой (
, тогда умножая первую строку на подходящие числа (для 2-ой ( 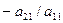 ), для 3-ей (
), для 3-ей ( 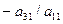 )) и прибавляя ее ко 2-ой и 3-ей и т. д. строкам. Преобразуем матрицу так, чтобы элементы первого столбца были равны нулю, тогда матрица примет вид:
)) и прибавляя ее ко 2-ой и 3-ей и т. д. строкам. Преобразуем матрицу так, чтобы элементы первого столбца были равны нулю, тогда матрица примет вид:


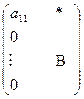 .
.
Рассмотрим матрицу 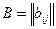 , образованную элементами 2-й, ..., n-й строк и столбцов. Добьемся того, чтобы
, образованную элементами 2-й, ..., n-й строк и столбцов. Добьемся того, чтобы 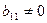 , переставляя местами строки. Если этого сделать нельзя, то матрица уже имеет ступенчатый вид. Проделаем те же операции, что и с матрицей А, и так до тех пор, пока матрица не примет вид (3.1).
, переставляя местами строки. Если этого сделать нельзя, то матрица уже имеет ступенчатый вид. Проделаем те же операции, что и с матрицей А, и так до тех пор, пока матрица не примет вид (3.1).
Пример 3.1. Найти ранг матрицы
А= 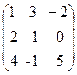 .
.
Решение.Приведем матрицу к ступенчатому виду:
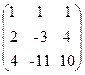 ~
~ 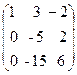 ~
~ 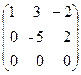 .
.
1. Умножим каждый элемент 1-ой строки на (-2) и сложим со второй строкой; на (-4) и сложим с третьей строкой.
2.Умножим каждый элемент 2-ой строки на (-3) и сложим с 3-ей строкой.
3. Нетрудно увидеть, что максимальный порядок миноров этой матрицы отличных от нуля равен двум, поскольку минор третьего порядка содержит элементы 3-ей строки, которые равны нулю, следовательно определитель третьего порядка равен нулю, таким образом r(A) = 2.
