Задачи для самостоятельного решения. Решить системы уравнений с помощью метода Гаусса:

Решить системы уравнений с помощью метода Гаусса:

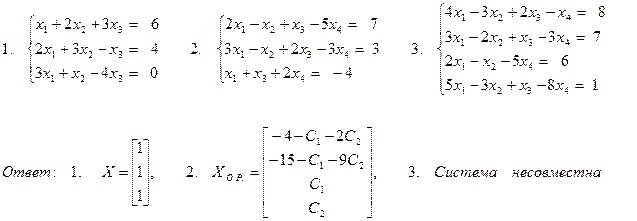
Исследование системы на совместность.

Решение произвольных СЛУ.

Рассмотрим систему (1) из m уравнений с n неизвестными.

Теорема Кронекера-Капелли. Для совместности системы (1) необходимо и достаточно, чтобы рангосновной матрицы той системы был равен рангу расширенной матрицы: .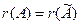

Теорема. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема. Система имеет множество решений, если ранг матрицы совместной системы меньше числа неизвестных.

В случае совместности систему (1) заменяют приведенной системой, т. е. равносильной ей системой, состоящей из r уравнений, коэффициенты которых образуют базисный минор. Остальные m-r уравнений вычеркиваются.

В случае r(А) < n выделяют базисные и свободные неизвестные. Базисными неизвестными являются любые r неизвестных, коэффициенты при которых образуют базисный минор. Остальные n-r неизвестных являются свободными. Затем систему (1) заменяют приведенной системой, причем базисные неизвестные оставляют в левой части, а свободные неизвестные переносят в правую часть.

Приведенная система всегда является невырожденной системой из r уравнений с r неизвестными. Для нахождения решения можно применять формулы Крамера, матричный метод или метод Гаусса.

Пример.

Исследовать систему на совместность и найти решение в случае совместности

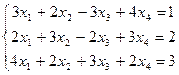
Данная система содержит m=3 уравнения и n=4 неизвестных.

А = 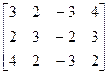, Ã=

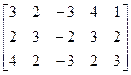
Найдем r(А) методом окаймляющих миноров: r(А) ≤n

M₂=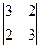 =5≠0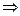r(A)≥2

M₃=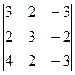 =5≠0r(A)=3 r(Ã)=3

Так как г(А) = г(А), то система является совместной и так как г < п, то система имеет бесконечное множество решений.

Базисный минор - М₃. Базисные неизвестные - х₁, х₂, х₃. Свободное неизвестное - х₄.

Заменяем исходную систему приведенной:

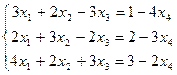
Получили невырожденную систему, далее используем формулы Крамера:

∆₁=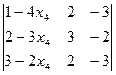 =10+10x₄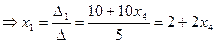

∆₂=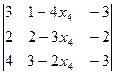 =4-x₄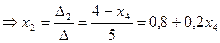

∆₃=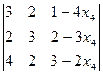 =11+16x₄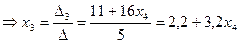

Заменим х₄ = С.

Ответ: Общее решение Х_O.P = ,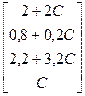

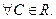
Пример.

Исследовать систему на совместность и найти решение в случае совместности

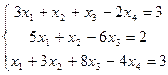
Найдем ранг матрицы системы и ранг расширенной матрицы методом элементарных преобразований. Составим расширенную матрицу и преобразуем ее:

1) переставим 1-ю и 3-ю строки;

2) поочередно домножаем 1-ю строку на -5 и -3 и прибавляем соответственно ко 2-й и 3-й строке:

~ ~

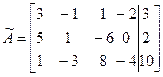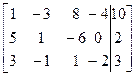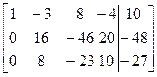
До вертикальной черты стоит матрица, эквивалентная А, тогда ранг r(А) = 2 (одну из пропорциональных строк можно вычеркнуть). Но матрица, эквивалентная Ã не содержит пропорциональных строк, поэтому продолжаем:

3) разделим 2-ю строку на 2;

4) вычтем 2-ю строку из 3-й;

5) домножаем 1-й столбец на 3, -8, 4 и прибавляем соответственно ко 2-му, 3-му, 4-му столбцу;

6) домножаем 2-й столбец поочередно на 23/8,-10/8 и прибавляем соответственно к 3-му и 4-му столбцу;

7) вычеркиваем нулевые столбцы:

~ ~ ~

~ ~

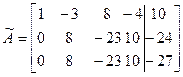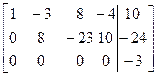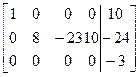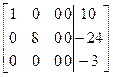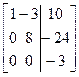
Таким образом ранг расширенной матрицы r(Ã) = 3.

Так как r(А)≠ r(Ã), то данная система несовместна, следовательно решений не имеет.