Б) Проверка домашнего задания (файл д_з.Doc загружен на компьютере).
Пример 1. Докажите тавтологию ((X  Y)
Y)  (Y
(Y  Z))
Z))  (X
(X  Z)
Z)
Решение.
| F1 | F2 | F3 |
| X | Y | Z | X  Y Y | Y  Z Z | X  Z Z | F1  F2 F2 | (F1  F2) F2)  F3 F3 |
Вывод. Высказывание ((X Y)
Y) (Y
(Y Z))
Z)) (X
(X Z) является тавтологий (тождественно-истинное высказывание).
Z) является тавтологий (тождественно-истинное высказывание).
Пример 2. Установить истинность высказывания.
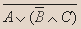
Решение.
| А | В | С | 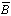 | 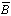  С С | А  ( ( 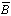  С) С) | 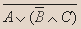 |
Вывод. Высказывание 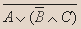 истинно, когда:
истинно, когда:
А) A  0; B
0; B  0; C
0; C  0; Б) A
0; Б) A  0; B
0; B  1; C
1; C  0; В) A
0; В) A  0; B
0; B  1; C
1; C  1.
1.
Пример 3.Эквивалентны ли высказывания:
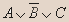 и
и 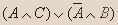
Решение.
| А | В | С | 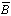 |  |  |  |  |   B B |  |
Вывод.
Высказывание  и высказывание
и высказывание  не эквивалентны.
не эквивалентны.
II. Составление таблиц истинности.
Упражнение 1. Из простых высказываний: “Виктор хороший пловец” - А; “Виктор хорошо ныряет” - В; “Виктор хорошо поет” - С, составлено сложное высказывание, формула которого имеет вид: X=(A  C)
C)  (A
(A  B). Установить, эквивалентно ли высказывание Х высказыванию: “Виктор - хороший пловец и Виктор хорошо поет”.
B). Установить, эквивалентно ли высказывание Х высказыванию: “Виктор - хороший пловец и Виктор хорошо поет”.
Решение. Y=A  C
C
| А | В | С | A  C C | A  B B | X | Y=A  C C |
Вывод. Высказывание X не эквивалентно высказыванию Y.
Упражнение 2. Установить является ли данное высказывание тавтологией.

| A | B | A  B B |  | 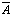 | 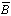 |  |  |
Вывод. Высказывание  является тавтологией.
является тавтологией.
Упражнение 3.Установить истинность высказываний:
а) ((X1  X2)
X2)  X3)
X3)  (X3
(X3  X1)
X1)
| F1 | F2 | F3 | ||||
| X1 | X2 | X3 | X1  X2 X2 | F1  X3 X3 | X3  X1 X1 | F2  F3 F3 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Вывод. Высказывание ((X1  X2)
X2)  X3)
X3)  (X3
(X3  X1) истинно, когда:
X1) истинно, когда:
1) X1  1; X2
1; X2  0; X3
0; X3  0; 2) X1
0; 2) X1  1; X2
1; X2  1; X3
1; X3  1
1
б) ((X  Y)
Y)  (Y
(Y  Z))
Z))  (X
(X  Z)
Z)
| F1 | F2 | F3 | F4 | ||||
| X | Y | Z | X  Y Y | Y  Z Z | F1  F2 F2 | X  Z Z | F3  F4 F4 |
Вывод. Высказывание ((X  Y)
Y)  (Y
(Y  Z))
Z))  (X
(X  Z) истинно всегда.
Z) истинно всегда.
Упражнение 4.Для формулы  придумайте формализуемое предложение.
придумайте формализуемое предложение.
Решение. Пусть А – «Петр замечательно играет в шахматы»; В — «Семен играет на баяне»; С — «Галина смотрит телевизор»
Тогда и только тогда если Петр замечательно играет в шахматы, то Семен не играет на баяне, когда Галина смотрит телевизор и Петр замечательно играет в шахматы.
Самостоятельная работа.
Вариант №1.
Установить истинность высказывания 
Решение.
| X | Y |  |  | X  Y Y |  |  |
2. Для формулы  придумайте формализуемое предложение.
придумайте формализуемое предложение.
3. Установите, является ли высказывание (X  Y)
Y) 
 тавтологией.
тавтологией.
Решение.
| X | Y | (X  Y) Y) |  |  |  | (X  Y) Y)   |
Вывод. Высказывание тавтологией не является.
4. Установите, эквивалентны ли высказывания?



Решение.
| A | B |  | 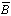 |  |  | A  B B |  |
Вывод. X1  X3
X3
Вариант №2.
1. Установить истинность высказывания 
Решение.
| X | Y | X  Y Y |  |  |  |  |
2. Для формулы  придумайте формализуемое предложение.
придумайте формализуемое предложение.
3. Установите, является ли высказывание 

 тавтологией.
тавтологией.
Решение.
| X | Y | X  Y Y |  |  |  |  |    |
Вывод. Высказывание тавтологией не является.
4. Установите, эквивалентны ли высказывания?

Решение.
| X | Y |  |  |  |  |  |  |  |
Вывод. A  B
B
IV. Подача нового материала. (Использоватьпрограмму MATLOG).
Равносильности формул логики высказываний часто называют законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств. Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям.
Перечислим наиболее важные из них:
- X
 X Закон тождества.
X Закон тождества. -
 Закон противоречия
Закон противоречия -
 Закон исключенного третьего
Закон исключенного третьего -
 Закон двойного отрицания
Закон двойного отрицания - Законы идемпотентности: X
 X
X  X, X
X, X  X
X  C
C - Законы коммутативности (переместительности): X
 Y
Y  Y
Y  X, X
X, X  Y
Y  Y
Y  X
X - Законы ассоциативности (сочетательности): (X
 Y)
Y)  Z
Z  X
X  (Y
(Y  Z), (X
Z), (X  Y)
Y)  Z
Z  X
X  (Y
(Y  Z)
Z) - Законы дистрибутивности (распределительности): X
 (Y
(Y  Z)
Z)  (X
(X  Y)
Y)  (X
(X  Z), X
Z), X  (Y
(Y  Z)
Z)  (X
(X  Y)
Y)  (X
(X  Z)
Z) - Законы де Моргана
 ,
, 
- X
 1
1  X, X
X, X  0
0  X
X - X
 0
0  0, X
0, X  1
1  1
1 - Законы поглощения: X
 (X
(X  Y)
Y)  X, X
X, X  (X
(X  Y)
Y)  X
X - Законы склеивания: (X
 Y)
Y)  (
( 
 Y)
Y)  Y, (X
Y, (X  Y)
Y)  (
( 
 Y)
Y)  Y
Y
1-й закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует.
Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. “Это яблоко спелое” и “Это яблоко не спелое”.
Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание.
Закон двойного отрицания.Отрицать отрицание какого-нибудь высказывания - то же, что утверждать это высказывание.
“ Неверно, что 2*2<>4”
Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых “сомножителей” равносильна одному из них.
Законы коммутативности и ассоциативности. Конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел.
В отличие от сложения и умножения чисел логическое сложение и умножение равноправны по отношению к дистрибутивности: не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции.
Смысл законов де Моргана (Август де Морган (1806-1871) - шотландский математик и логик) можно выразить в кратких словесных формулировках:
 - отрицание логического произведения эквивалентно логической сумме отрицаний множителей.
- отрицание логического произведения эквивалентно логической сумме отрицаний множителей.
 - отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых.
- отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых.
Доказать законы логики можно:
- с помощью таблиц истинности;
- с помощью равносильностей.
Докажем законы склеивания и поглощения с помощью равносильностей:
- (X
 Y)
Y)  (
( 
 Y)
Y)  (X+Y) *(
(X+Y) *(  +Y)
+Y)  X*
X*  + Y*
+ Y*  + Y*Y+ X*Y
+ Y*Y+ X*Y  Y*
Y*  + Y + X*Y
+ Y + X*Y  Y*
Y*  + Y(1+X)
+ Y(1+X)  Y*
Y*  +Y
+Y  Y(
Y(  +1)
+1)  Y склеивания
Y склеивания - X
 (X
(X  Y)
Y)  X*X+X*Y
X*X+X*Y  X+X*Y
X+X*Y  X(1+Y)
X(1+Y)  X поглощения
X поглощения
Домашнее задание.
1. Является ли высказывание (X  Y)
Y)  (Y
(Y  X) тавтологией.
X) тавтологией.
2. Установить эквивалентны ли высказывания.

3. С помощью таблиц истинности доказать законы поглощения и склеивания.
