Разложение функций в степенные ряды

ГЛАВА III РЯДЫ

ЧИСЛОВЫЕ РЯДЫ

Пусть u₁,u₂,u₃,…u_n,…— бесконечная числовая по­следовательность. Выражение

u₁+u₂+u₃+…..+u_n+…

называется бесконечным числовым рядом, а числа u₁,u₂,u₃,…u_n,….— членами ряда; и_п=f(п) называется общим членом. Ряд часто записывают в виде .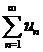

Сумму первых п членов числового ряда обозначают через S_n и называют n-й частичной суммой ряда:

S_n= u₁+u₂+u₃+…..+u_n.

Ряд называется сходящимся, если его n-я частичная сумма S_n при неогра­ниченном возрастании п стремится к конечному пределу, т. е. если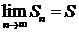

Число S называют суммой ряда. Если же n-я частичная сумма ряда при 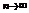не стремится к конечному пределу, то ряд называют расходящимся.

Ряд а+aq+aq²+…+aq^n-1+…(|q|<1),

составленный из членов любой убывающей геометрической прогрессии, яв­ляется сходящимся и имеет сумму a/(1—q).

Ряд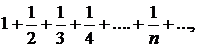

называемый гармоническим, расходится.

Приведем основные теоремы о сходящихся числовых рядах.

1. Если сходится ряд

u₁+u₂+u3+…,

то сходится и ряд

u_m+1+u_m+2+u_m+3+…

получаемый из данного ряда отбрасыванием первых т членов (этот последний ряд называют т-м остатком исходного ряда); наоборот, из сходимости т-го остатка ряда вытекает сходимость данного ряда.

2. Если сходится ряд

u₁+u₂+u₃+…,

и суммой его является число S, то сходится и ряд

au₁+au₂+au₃+…,

причем сумма последнего ряда равна аS.

3. Если сходятся ряды

u₁+u₂+u₃+…,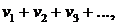

имеющие соответственно суммы S и s, то сходится и ряд

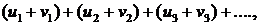
причем сумма последнего ряда равна S +s.

4. Если ряд

u₁+u₂+u₃+…

сходится, то 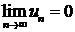при пр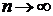едел общего члена сходящегося

ряда равен нулю (необходимый признак сходимости ряда).

Таким образом, если 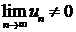, то ряд расходится.

Перечислим важнейшие признаки сходимости и расходимости рядов с по­ложительными членами.

Первый признак сравнения. Пусть даны два ряда

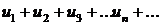(1)

и

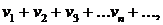(2)

причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т. е. 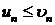(n=1, 2, 3, ...). Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).

Этот признак остается в силе, если неравенства 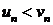выполняются не при всех n, а лишь начиная с некоторого номера n = N.

Второй признак сравнения. Если существует конечный и от-

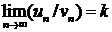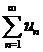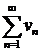личный от нуля предел то оба ряда и одновременно сходятся или одновременно расходятся.

Признак Коши. Если для ряда

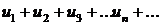
существует 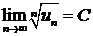, то этот ряд сходится при С < 1 и расходится

при С > 1.

Признак Даламбера. Если для ряда

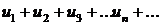
существует 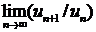= D, то этот ряд сходится при D< 1 и расходится

при D > 1.

Интегральный признак. Если F(х) при 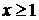—непрерывная, положительная и монотонно убывающая функция, то ряд 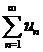где u_n=f(n), сходится или расходится в зависимости от того, сходится или расходится интеграл

Рассмотрим теперь ряды, члены которых имеют чередующиеся знаки, т. е. ряды вида

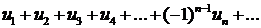
где u_n>0 (n=1, 2, 3, ...),

Признак сходимости знакочередующегося ряда (приз­нак Лейбница). Знакочередующийся ряд сходится, если абсолютные вели­чины его членов монотонно убывают, а общий член стремится к нулю, т. е. если выполняются следующие два условия: 1) и_г > и₂ > и₃ >... и 2)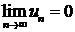

Возьмем n-ю частичную сумму сходящегося знакочередующегося ряда, для которого выполняется признак Лейбница:

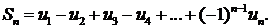
Пусть R_n—n-й остаток ряда. Его можно записать как разность между сум­мой ряда S и п-й частичной суммой S_n т. е. R_n=S-S_n Нетрудно видеть, что

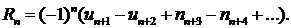
Величина | 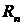|оценивается с помощью неравенства | 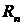| < u_n+1

Остановимся теперь на некоторых свойствах знакопеременных рядов

(т. е. знакочередующихся рядов и рядов с произвольным чередованием знаков

своих членов).

Знакопеременный ряд

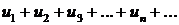
сходится, если сходится ряд

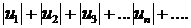
В этом случае исходный ряд 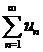называется абсолютно сходящимся.

Сходящийся ряд 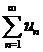называется условно сходящимся, если ряд 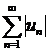расходится.

Если ряд 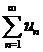абсолютно сходится, то ряд, полученный после любой перестановки бесконечного множества его членов, абсолютно сходится и имеет ту же сумму, что и первоначальный ряд.

Если ряд 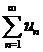условно сходится, то при перестановке бесконечного множества его членов сумма ряда может измениться. В частности, при соот­ветствующей перестановке членов условно сходящегося ряда можно превра­тить его в расходящийся ряд.

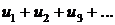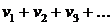Если ряды и сходятся абсолютно и имеют соответственно суммы S1 и S₂, то сходится абсолютно и ряд

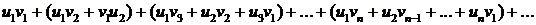
Этот ряд называется произведением рядов (по Коши). Его сумма равна S₁S₂.

269.Дан общий член ряда 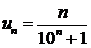. Написать первые че­тыре члена ряда.

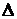Если n=1, то u₁=1/11; если n=2, то u₂=2/101; если n=3, то
u₃=3/1001; если n= 4, то u₄ = 4/10001;….. Ряд можно записать в виде

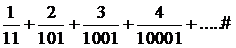
270.Найти общий член ряда

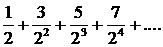
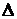Последовательные числители образуют арифметическую прогрессию 1, 3, 5, 7 ...; n-й член прогрессии находим по формуле a_n=a₁+d(n-1). Здесь а₁=1, d=2поэтому a_n=2п—1. Последовательные знаменатели обpазуют геометрическую прогрессию 2, 2², 2³, 2⁴, ...; n-й член этой прогрессии b_n=2ⁿ. Следовательно, общий член ряда и_п = (2п—1)/2ⁿ.

Вообще нужно иметь в виду, что несколько первых членов ряда полностью ряд не определяют.

271.Найти общий член ряда

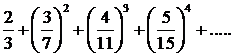
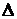Показатель степени каждого члена совпадает с номером этого члена, поэтому показатель степени п-го члена равен п. Числители дробей 2/3, 3/7, 4/11, 5/15,... образуют арифметическую прогрессию с первым членом 2 и разностью 1. Поэтому п-й числитель равен n+1. Знаменатели образуют арифметическую прогрессию с первым членом 3 и разностью 4. Следовательно, n-й знаменатель равен 4n-1. Итак, общим членом ряда является

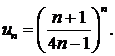
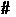
272.Найти сумму ряда

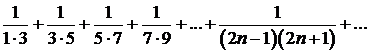
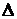Общий член ряда можно представить в следующем виде:

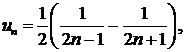
откуда

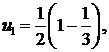
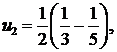
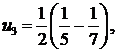
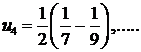
Следовательно,

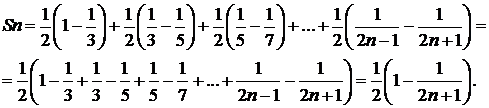
Так как 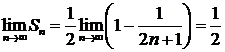, то ряд сходится и его сумма равна 1/2.▲

Найти сумму ряда

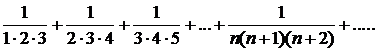
∆ Представим общий член ряда и_п в виде суммы простейших дробей:

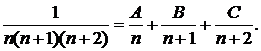
Умножая обе части этого выражения на знаменатель, придем к тождеству

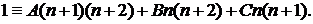
Полагая последовательно n = 0, —1, —2, находим: при n=0: 1=2A; A = 1/2; при n = -1: 1 = -В; В = -1; при n = —2: 1=2С, С=1/2. Таким образом,

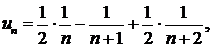т.е.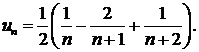

Отсюда

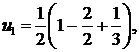
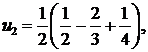
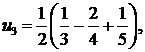
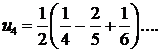
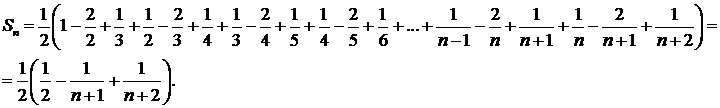
Итак, 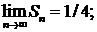следовательно, ряд сходится и имеет сумму 1/4. ▲

274. Исследовать сходимость ряда

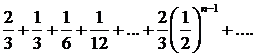
∆ Данный ряд составлен из членов бесконечно убывающей геометри­ческой прогрессии и поэтому сходится. Найдем его сумму. Здесь а = 2/3, q= 1/2 (знаменатель прогрессии). Следовательно,

▲

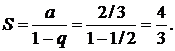Исследовать сходимость ряда

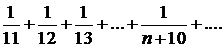
∆Данный ряд получен из гармонического отбрасыванием первых десяти членов. Следовательно, он расходится. ▲

276. Исследовать сходимость ряда

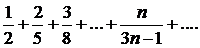
∆ Так как

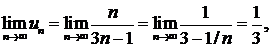
т. е. 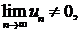то ряд расходится (не выполняется необходимый признак сходимости). ▲

277. Исследовать сходимость ряда

0,6 + 0,51 +0,501 + ... +[0,5+ (0,1)ⁿ]+ ....

∆ Здесь 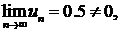и ряд расходится. ▲

278. Исследовать сходимость ряда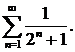

∆Члены данного ряда меньше соответствующих членов ряда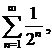

т. е. ряда 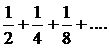Но последний ряд сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, сходится и данный ряд. ▲

279. Исследовать сходимость ряда

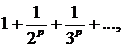если р<1.

∆ Члены этого ряда, начиная со второго, больше соответствующих чле­нов гармонического ряда. Следовательно, ряд расходится.▲

280. Исследовать сходимость ряда с общим членом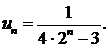

∆Сравним этот ряд с рядом, у которого общий член 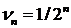(т. е. с бесконечно убывающей геометрической прогрессией). Применим второй признак сравнения рядов:

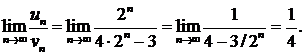
Так как предел конечен и отличен от нуля и ряд 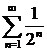сходится, то сходится и данный ряд. ▲

281. Исследовать сходимость ряда

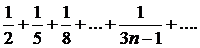
∆ Сравним ряд с гармоническим рядом, у которого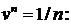

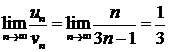
Следовательно, данный ряд расходится. ▲

282. Исследовать сходимость ряда

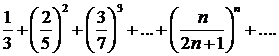
∆ Здесь удобно применить признак Коши, поскольку 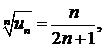а предел последней дроби находится просто:

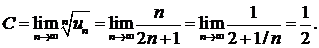
Так как С = 1/2 < 1, то ряд сходится. ▲

283. Исследовать сходимость ряда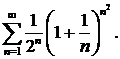

∆ Снова применим признак Коши:

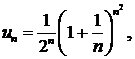
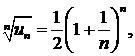
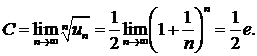
Так как С > 1, то ряд расходится. ▲

284.Исследовать сходимость ряда

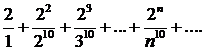
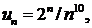
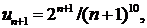
∆ Применим признак Даламбера; имеем 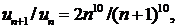значит,

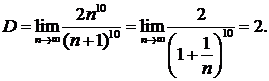
Так как D > 1, то ряд расходится. ▲

285. Исследовать сходимость ряда

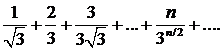
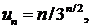
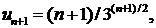
∆ Здесь 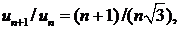поэтому

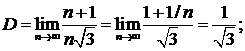D<1.

Следовательно, ряд сходится. ▲

286. Исследовать сходимость ряда

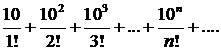
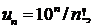
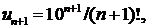
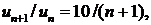
∆ Имеем 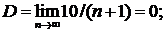D<1.

—ряд сходится. ▲

287. Исследовать сходимость рядa

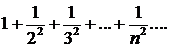
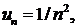
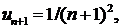
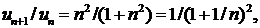
∆ Имеем 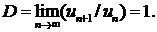Так как D = 1, то с помощью признака Даламбера не удается решить вопроса о сходимости ряда.

Применим интегральный признак: 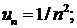следовательно, f(х) = 1/х³,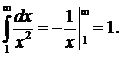

Интеграл сходится (является конечной величиной), поэтому сходится и данный ряд.▲

288. Исследовать сходимость ряда

∆ Применим интегральный признак:

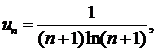
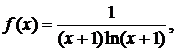
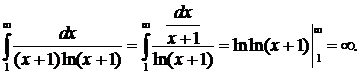
Интеграл расходится, поэтому расходится и данный ряд. ▲

289. Исследовать сходимость ряда

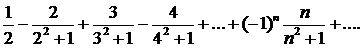
∆ Применим признак Лейбница. Так как

…..

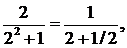
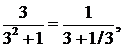
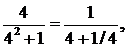то

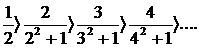
Следовательно, выполнено первое условие признака Лейбница. Далее, так как

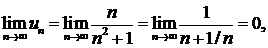
то выполнено и второе условие. Значит, данный ряд сходится. ▲

290. Исследовать сходимость ряда

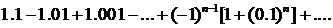
∆ Первое условие признака Лейбница выполняется: 1,1 > 1,01 > 1,001 > >...; с другой стороны, 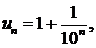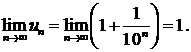Так как 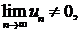то не выполнен необходимый признак сходимости ряда. Ряд расходится. ▲

291. Исследовать сходимость ряда

.

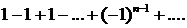∆ Общий член ряда не стремится к нулю, поэтому ряд расходится. ▲

292.Исследовать сходимость ряда

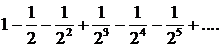
∆ Составим ряд из абсолютных величин:

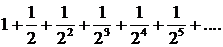
Этот ряд есть бесконечно убывающая геометрическая прогрессия и, следова­тельно, сходится. Значит, и данный ряд сходится, причем абсолютно. ▲

293.Найти произведение абсолютно сходящихся рядов

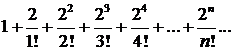
и

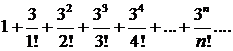
∆ Произведение рядов (согласно данному на с. 68 определению) есть ряд

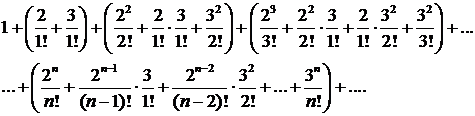
или

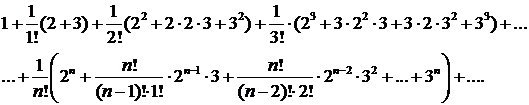
Так как 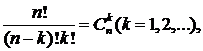то ряд можно переписать в виде

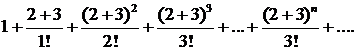
или

▲

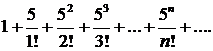294.Написать первые четыре члена ряда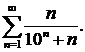

295.Написать первые четыре члена ряда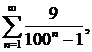

Найти суммы рядов:

296.

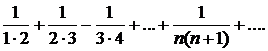
297.

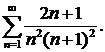
298.

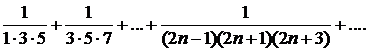
299.

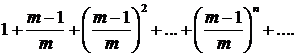
300.Показать, что ряд 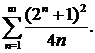расходится.

Исследовать сходимость рядов с помощью первого признака сравнения:

301.

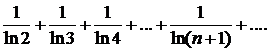
302.

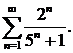
Исследовать сходимость рядов с помощью второго признака сравнения:

303.

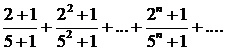
●Сравнить с рядом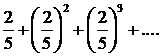

304.

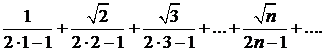
Пользуясь признаком Коши, исследовать сходимость рядов:

305.

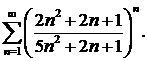
306. 3 + (2,1)² + (2,01)³+...+[2 + (0_,1)^n-1]+...

Пользуясь признаком Даламбера, исследовать сходимость рядов:

307.

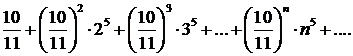
308.

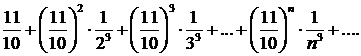
Пользуясь интегральным признаком, исследовать сходимость рядов:

309. 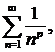если р>1.

310.

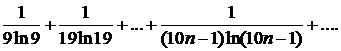
Исследовать сходимость знакопеременных рядов и установить характер сходимости (абсолютная, условная):

311.

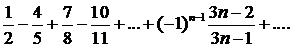
312.

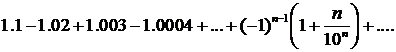
313.

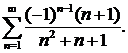
314.

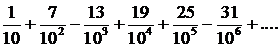
315.

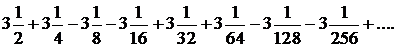
Исследовать сходимость рядов:

316.

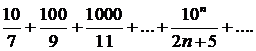
317.

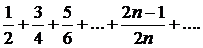
318.

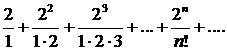
319.

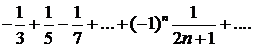
320.

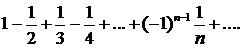
321.

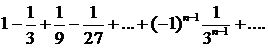
322.

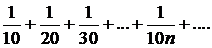
323.

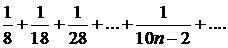
324.

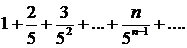
325.

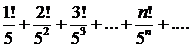
326.

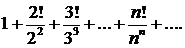
327.

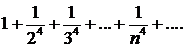
328.

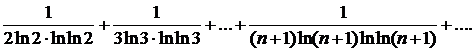
329.

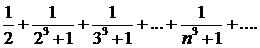
330.

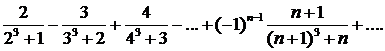
331.

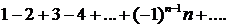
332.

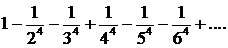
333.

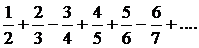
334.

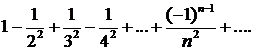
335.

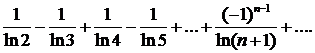
336. Найти произведение абсолютно сходящихся рядов 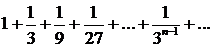и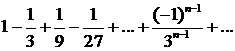

337.Показать, что ряд 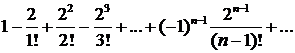абсолютно сходится, и возвести его в квадрат (умножить на себя).

ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Ряд

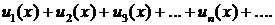
члены которого—функции от х, называется функциональным. Совокупность значений х, при которых функции и₁(х), и₂(х), ..., u_n(x)... определены и ряд 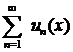сходится, называют областью сходимости функционального ряда. Областью сходимости функционального ряда чаще всего служит какой-нибудь промежуток оси Ох. Каждому значению из области сходимости X соответствует определенное значение величины 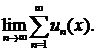Эту величину, являющуюся функцией х, называют суммой функционального ряда и обозна­чают через S(х).

Представим сумму ряда в виде S(х) = S_n(х)+R_п (х), где

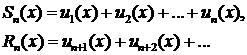
[R_n(x)— остаток функционального ряда].

Сходящийся функциональный ряд 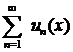называется равномерно сходящимся в некоторой области X, если для каждого сколь угодно малого числа δ > 0 найдется такое целое положительное число N, что при п≥N выпол­няется неравенство /R_n (х)/ <δ для любого х из области X. При этом сумма S (x) равномерно сходящегося ряда 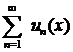в области X, где и_n (х) (п=1, 2, 3, ...)—непрерывные функции, есть непрерывная функция.

Сформулируем достаточный признак равномерной сходимости функцио­нального ряда — признак Вейерштрасса.

Если функции и₁(х), и₂(х), …, и_п(х), ... по абсолютной величине не превосходят в некоторой области X положительных чисел а₁, а₂, ...,а_n, ..., причем числовой ряд

a₁+a₂+a₃+…+a_n+…

сходится, то функциональный ряд

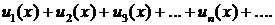
в этой области сходится равномерно.

В заключение сформулируем две теоремы, относящиеся к интегрированию и дифференцированию функциональных рядов.

1. Если 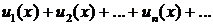, где u₁ (x), и₂(х), ..., и_n (х), ... —непрерывные функции, равномерно сходится в некоторой области X и имеет сумму S (х), то ряд

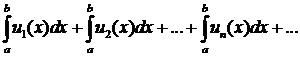
сходится и имеет сумму 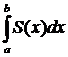(промежуток [а, b] принадлежит области X).

2. Пусть функции 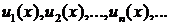определены в некоторой области X и имеют в этой области производные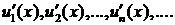

Если в этой области ряд 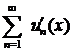сходится равномерно, то его сумма равна производной от суммы первоначального ряда:

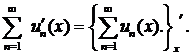
338.Дан функциональный ряд

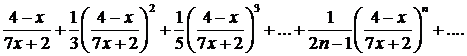
Исследовать сходимость ряда в точках х=0 и х=1.

∆ В точке х=0 получаем ряд

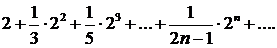
Здесь u_n= 2ⁿ/(2n—1), u_n+1 = 2ⁿ⁺¹/(2n+1). Применяем признак Даламбера:

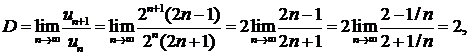
т. е. D > 1. Следовательно, ряд расходится.

В точке х=1 получаем ряд

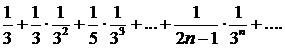
Здесь 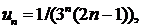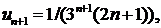находим

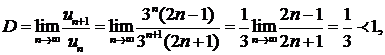
т. е. ряд сходится. ▲

339.Найти область сходимости ряда

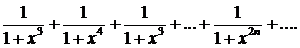
∆Если |x|< 1, то 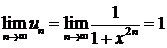; так как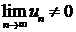

ряд расходится. Если |x|=1, то также получаем расходящийся ряд

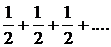
Если |х| > 1, то члены заданного ряда меньше членов бесконечно убы­вающей геометрической прогрессии 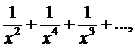т.е. ряд сходится.

Итак, область сходимости ряда определяется неравенством |д;|> 1. От­сюда следует, что ряд сходится, если 1 < x < +∞ или —∞ < х < —1. ▲

340.Показать, что ряд

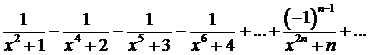
сходится равномерно при всех значениях х(-∞<x<∞).

∆ Данный ряд при любом значении х сходится по признаку Лейбница, поэтому его остаток оценивается с помощью неравенства |R_п(х)| < |и_п+1(х)|, т. е.

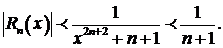
Так как неравенства 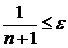и 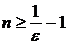равносильны, то, взяв 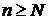, где

N—какое-нибудь целое положительное число, удовлетворяющее условию
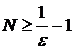, приходим к неравенству |R_п(х)| < 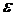. Итак, данный ряд сходится

равномерно в промежутке (—∞, +∞). ▲

341. Показать, что ряд 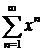сходится неравномерно в ин-

тервале (—1, 1).

Δ В указанном интервале ряд сходится как бесконечно убывающая гео­метрическая прогрессия. Имеем 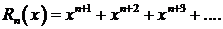, т. е. .

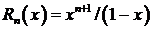Но 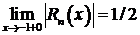, 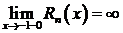. Следовательно,

приняв 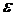<1/2, мы не сможем добиться выполнения неравенства при любом

значении х. Итак, ряд 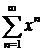сходится неравномерно. ▲

341.С помощью признака Вейерштрасса показать, что ряд

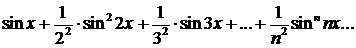
сходится равномерно в промежутке (—∞, +∞).

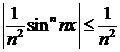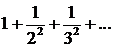Δ Так как и ряд сходится, то дан-

ный ряд сходится равномерно при любых значениях х. ▲

343.Можно ли к ряду

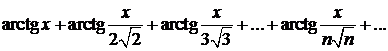
применить теорему о почленном дифференцировании рядов?

Δ Сравним данный ряд со сходящимся рядом

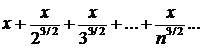
(при любом фиксированном х). Тогда , .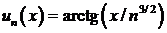

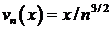Так как 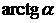и 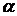— эквивалентные бесконечно малые, то 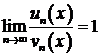и

согласно второму признаку сравнения заключаем, что данный ряд сходится. Найдем производную общего члена данного ряда:

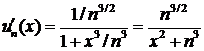
Ряд, составленный из производных, имеет вид

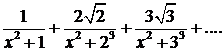
Заметим, что члены последнего ряда меньше соответствующих 'членов сходящегося ряда 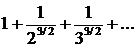Поэтому на основании признака Вейерштрасса ряд, составленный из производных, равномерно сходится в про­межутке (—∞, +∞) и, значит, к заданному ряду можно применить теорему о дифференцировании рядов. ▲

344.Законно ли применение к ряду

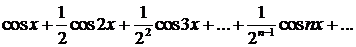
теоремы об интегрировании функциональных рядов в промежутке ?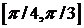

Δ Члены заданного ряда при любом значении х по абсолютной величине меньше соответствующих членов бесконечно убывающей геометрической прог­рессии 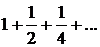Поэтому данный ряд согласно признаку Вейершт­расса равномерно сходится в промежутке (—∞, +∞) и, следовательно, к нему можно применить теорему об интегрировании рядов для любого конеч­ного промежутка [а, b], в частности, для промежутка . ▲

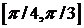345.Дан функциональный ряд

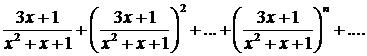
Сходится ли ряд в точках х=1, х=2 и х=3?

346.Исследовать сходимость функционального ряда

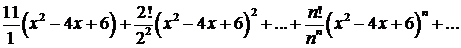
в точках x:=1 и х=2.

347.Найти область сходимости ряда

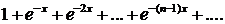
348. Найти область сходимости ряда

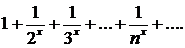
348.Найти область сходимости ряда

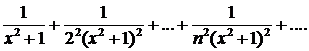
350. Показать, что ряд 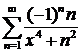равномерно сходится в

промежутке (—∞, +∞).

351.Показать, что ряд

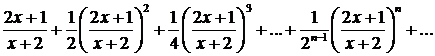
равномерно сходится в промежутке [—1, 1].

352. Показать, что ряд

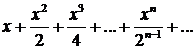
в интервале (—2, 2) сходится неравномерно.

353. Показать, что ряд

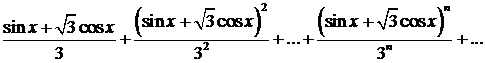
сходится в промежутке(—∞, +∞) и установить характер схо­димости.

354. Можно ли к ряду

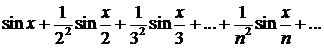
применить теорему о дифференцировании функциональных рядов?

355. Можно ли к ряду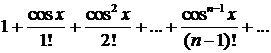

применить теорему об интегрировании функциональных рядов в любом конечном промежутке [а, b]?

356. Можно ли к ряду

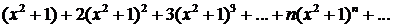
применить теорему о дифференцировании функциональных рядов?

СТЕПЕННЫЕ РЯДЫ

Функциональный ряд вида

a₀+a₁(x-a)+a₂(x-a)²+…+a_n(x-a)ⁿ

где a₀ , a₁,… a_n - действительные числа, называется степенным.

Основное свойство степенных рядов состоит в том, что если степенной ряд сходится при х=х₀, то он сходится (и притом абсолютно) при всяком значе­нии х, удовлетворяющем неравенству|х—а| < |х₀—а| (теорема Абеля).

Одним из следствий теоремы Абеля является факт существования для всякого степенного ряда интервала сходимости |х—а| < R, или а—R < х < a+R с центром в точке а, внутри которого степенной ряд абсолютно схо­дится и вне которого он расходится. На концах интервала сходимости (в точ­ках x= а ± R) различные степенные ряды ведут себя по-разному: одни схо­дятся абсолютно на обоих концах, другие—либо условно сходятся на обоих концах, либо на одном из них условно сходятся, на другом расходятся, третьи— расходятся на обоих концах.

Число R—половина длины интервала сходимости—называется радиусом сходимости степенного ряда. В частных случаях радиус сходимости ряда R может быть равен нулю или бесконечности. Если R = 0, то степенной ряд сходится лишь при х=а; если же R = ∞, то ряд сходится на всей числовой оси.

Для отыскания интервала и радиуса сходимости степенного ряда можно пользоваться одним из следующих способов.

1. Если среди коэффициентов ряда a₁,a₂…a_nнет равных нулю,
т. е. ряд содержит все целые положительные степени разности х—а, то

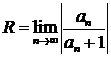(1)

при условии, что этот предел (конечный или бесконечный) существует.

2. Если исходный ряд имеет вид

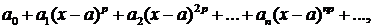.... (где р—некоторое определенное целое положительное число: 2, 3, ...), то

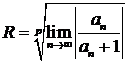(2)

2. Если среди коэффициентов ряда есть равные нулю и последовательность
оставшихся в ряде показателей степеней разности х—а любая (т. е. не обра­
зует арифметическую прогрессию, как в предыдущем случае), то радиус схо­
димости можно находить по формуле

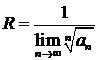(3)

в которой используются только значения a_n отличные от нуля. (Эта формула пригодна и в случаях 1 и 2.)

4. Во всех случаях интервал сходимости можно находить, применяя не­
посредственно признак Даламбера или признак Коши к ряду, составленному
из абсолютных величин членов исходного ряда.

Записав ряд в виде

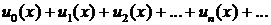
(здесь и₀ = а₀, и_п(х)=а_п(х—а)^N, где зависимость N от п может быть любой, причем через а_п обозначен не коэффициент при (х—а)", а коэффициент n-го члена ряда), находят интервал сходимости из неравенств

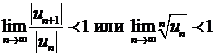
Отметим следующее свойство степенных рядов: ряды, полученные почлен­ным дифференцированием и интегрированием степенного ряда, имеют тот оке интервал сходимости и их сумма внутри интервала сходимости равна соот­ветственно производной и интегралу от суммы первоначального ряда.

Таким образом, если 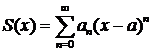, то

,

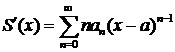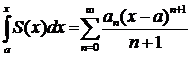
где —R < х—а < R.

Операцию почленного дифференцирования и интегрирования можно про­изводить над степенным рядом сколько угодно раз. Следовательно, сумма степенного ряда внутри его интервала сходимости является бесконечно диф­ференцируемой функцией.

357.Исследовать сходимость степенного ряда

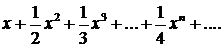
∆ Здесь а_п=1/п, а_п+1= 1/(n+ 1). Найдем радиус сходимости ряда:

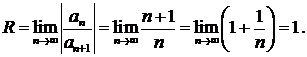
Следовательно, ряд сходится для значений х, удовлетворяющих неравен­ству —1 < х < 1.

Исследуем сходимость ряда на концах промежутка. Если х=1, то полу­чаем гармонический ряд 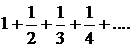который, как известно, расходится. Если х=-1, то получаем ряд 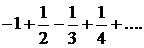Этот ряд сходится, так как удовлетворяет условиям признака Лейбница.

Итак, область сходимости степенного ряда определяется двойным неравен­ством -1≤x<1.▲

358.Исследовать сходимость ряда

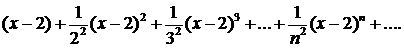
∆ Здесь a_n =1/n² , a_n+1 =1/(n+1)², имеем

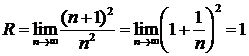
Следовательно, ряд сходится, если —1 < x — 2 < 1, т. е. 1 < х < 3.

Исследуем сходимость ряда на концах промежутка. Если х = 3, то полу­чаем ряд 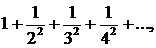который сходится, так как ряд 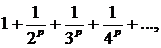сходится при р > 1 (на основании интегрального признака).

Если х=1, то получаем ряд 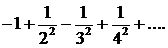Этот ряд сходится (и притом абсолютно), так как сходится ряд из абсолютных величин его членов. Итак, степенной ряд сходится для значений х, удовлетворяющих двой­ному неравенству 1 ≤ х ≤3. ▲

359. Исследовать сходимость ряда