Разложение функций в степенные ряды 1 страница

Оглавление

Раздел XI. Ряды.. 4

Числовые ряды − основные понятия. 4

Положительные ряды.. 12

Знакочередующиеся ряды.. 23

Знакопеременные ряды.. 27

Функциональные ряды.. 30

Степенные ряды.. 32

Разложение функций в степенные ряды.. 41

Разложения элементарных функций в ряды Маклорена. 45

Сборник задач по курсу. 50

Вопросы и задачи для самопроверки. 64

Примерный список вопросов для подготовки к экзаменам.. 71

Список рекомендуемой литературы.. 73

Словарь терминов. 74

Раздел XI. Ряды

Числовые ряды − основные понятия

До сих пор мы умели складывать только конечный набор чисел, пусть и очень большой : 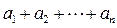. Когда-то считалось, что складывать бесконечный набор чисел бессмысленно, так как казалось очевидным, что складывая бесконечно много, например, положительных чисел, должна получаться бесконечная сумма. На этом казалось бы верном утверждении строились многие известные парадоксы (например, «Ахилл и черепаха»). Однако во многих практических задачах и чисто математических построениях возникали суммы бесконечного набора чисел, что привело к необходимости сделать их предметом исследования математики. Приведем пример практической задачи, в которой (в одном из подходов к ее решению) возникает необходимость сложения бесконечного набора чисел.

Пример 1. Допустим, что при добыче нефти десятая ее часть идет на обеспечение самой добычи (механизмы, обеспечивающие добычу, работают на бензине, который производится из нефти). Сколько необходимо добыть нефти, чтобы можно было продать 10 тонн?
Решение. Ясно, что нужно добыть, по крайней мере, эти 10 тонн. Но тогда нужно добавочно добыть 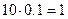тонну для обеспечения добычи этих 10 тонн. Но для обеспечения добычи этой 1 тонны необходимо добавочно добыть 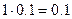тонны. Но для обеспечения ее добычи нужно еще добыть 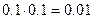тонны. И так далее. Таким образом, общее количество добытой нефти должно быть равно

(1)

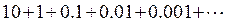
Таким образом, при таком подходе к решению возникла необходимость сложить бесконечный набор чисел.

Замечание. Конечно, предложенный выше подход к решению примера имеет чисто иллюстративную цель (естественное появление бесконечной суммы), поскольку очевиден следующий более простой путь решения. Пусть 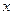− необходимое количество нефти, которое нужно добыть, чтобы на продажу иметь 10 тонн. Тогда 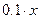тонн из добытого пойдет на обеспечение самой добычи. Таким образом, продать можно будет только 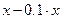тонн. Откуда получаем уравнение : 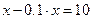, откуда 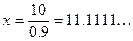тонн.

Приступим все же к понятию бесконечных сумм. Выражение вида

(2)

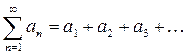
называется числовым рядом. Числа 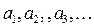называются членами (или слагаемыми) ряда.Выражение для a_n под знаком суммы в (2), позволяющее найти любое слагаемое по его порядковому номеру 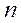, называется общим членом ряда. При подстановке в это выражение n=1, 2, 3, … получаем значения, соответственно, 1-го слагаемого, 2-го, 3-го ... . Например, ряд (1) можно с использованием знака суммы записать в виде 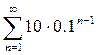, а потому общий член этого ряда имеет вид: 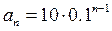. Действительно, подставляя в (2) n=1, 2, 3, … получаем значения, соответственно, 1-го слагаемого, 2-го, 3-го и т.д. слагаемого ряда (1).

Пример 2. Рассмотрим ряд 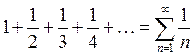− так называемый гармонический ряд. Числа 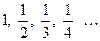являются членами ряда, а выражение 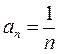является общим членом ряда.

Как же определить сумму ряда 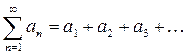, т.е. сумму бесконечного набора слагаемых? Можно поступить аналогично тому, как мы определяли несобственный интеграл по бесконечному промежутку или площадь неограниченной фигуры. Будем складывать бесконечный набор чисел «постепенно». Сначала составим «сумму» из одного первого слагаемого: S₁=a₁. Потом сложим первые 2 слагаемых: S₂=a₁+а₂. Потом первые 3 слагаемых:
S₃=a₁+а₂+а₃ и так далее. И будем следить за поведением бесконечной последовательности чисел S₁, S₂, S₃ … . Если эта последовательность сумм все увеличивающегося числа слагаемых ряда (2) приближается к определенному числу (т.е. имеет предел), то это число естественно назвать суммой всего ряда. Если же не приближается ни к какому числу (или идет к бесконечности), то естественно считать, что такой ряд суммы не имеет . Число 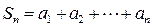называется n-ой частичной суммой ряда (n=1, 2, 3, ...) . Итак, ряд 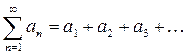называется сходящимся, если существует (конечный) предел его частичных сумм: 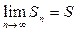. В этом случае число S называется суммой ряда, что записывается как 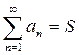. Если же такого предела не существует (или он равен ∞), то ряд называется расходящимся (такой ряд суммы не имеет).

Пример 3. Исследуем на сходимость следующий ряд

(3) .
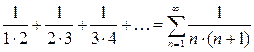Решение. Вычислим несколько первых последовательных частичных сумм и попробуем найти закономерность:

(4) , …

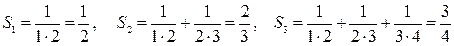Легко, глядя на (4), угадать общую формулу для частичных сумм: 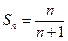(можно доказать эту формулу строго методом математической индукции). Тогда

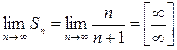={делим числитель и знаменатель на } .

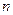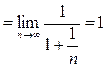Поэтому приведенному выше определению данный ряд (3) сходится, а его сумма равна 1: .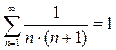

Пример 4. Пусть число 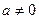. Рассмотрим ряд

(5) .

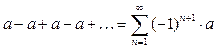Тогда S₁=a, S₂=0, S₃=a, S₄=0, S₅=a и так далее. Понятно, что такая последовательность частичных сумм 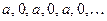предела не имеет, поэтому ряд (5) расходится.

Пример 5. (геометрическая прогрессия). Напомним, что геометрической прогрессией называется числовая последовательность, каждый член которой (начиная со второго) равен предыдущему, умноженному на одно и то же для этой последовательности число q (которое называется знаменателем данной прогрессии). Если обозначить а − первый член прогрессии, то прогрессия (по определению) имеет вид: a, aq, aq², … ,aqⁿ, … . Соответствующий ряд имеет вид
a + aq+ aq²+ … + aqⁿ+ … = 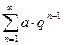( или 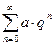, если начать нумерацию слагаемых не с единицы, а с нуля). Отметим сразу, что если знаменатель прогрессии 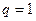, то соответствующий ряд 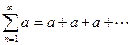расходится, поскольку его частичные суммы имеют вид 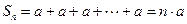, а потому 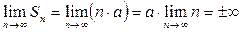в зависимости от знака числа 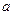. Для 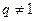из школьной программы известна общая формула для суммы первых n слагаемых геометрической прогрессии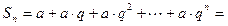 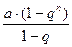. Поэтому, переходя к пределу 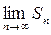, легко получить:

.

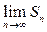
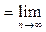
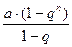
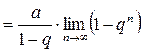
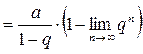Несложно выяснить, что предел 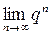существует (и при этом равен нулю) только в том случае, если 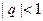. Отсюда следует, что ряд, составленный из геометрической прогрессии, сходится (и имеет суммой число 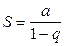) только тогда, когда 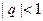. В этом случае геометрическая прогрессия называется бесконечно убывающей геометрической прогрессией и для нее

(6) = .

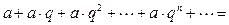
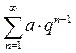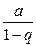Заметим, что ряд (1) тоже является бесконечно убывающей геометрической прогрессией с 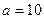и 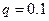, а потому из (6) получаем для примера 1, что необходимо добыть 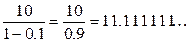тонн нефти, что выше было получено из простого алгебраического уравнения.

Рассмотрим свойства сходящихся рядов. Они напоминают свойства конечных сумм.

1. Если сходится ряд 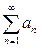, то для любого числа с сходится ряд 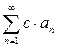и выполнено:

(7) = .

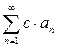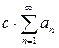Фактически это означает возможность вынесения общего множителя 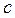за скобку (точнее, за знак суммы).

2. Если сходятся ряды 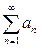и 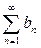, то сходится и ряд 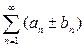и выполняется:

(8) = ± .

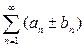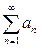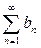Справедливость этих свойств легко доказывается из определения сходящихся рядов и соответствующих свойств пределов последовательностей (предел суммы-разности равен сумме-разности пределов, а постоянный множитель можно выносить за знак предела).

Пример 6. Вычислить сумму ряда .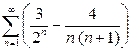
Решение. Используя свойство (8), а затем (7), последовательно получаем:

(9) .

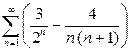
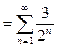
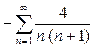
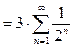
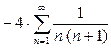Ряд 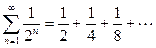есть сумма бесконечно убывающей геометрической прогрессии вида (6) с первым членом 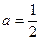и знаменателем 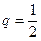, а потому по формуле (6): 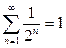. Сумма ряда 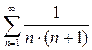была вычислена в примере 3: 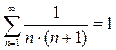. Окончательно, из (9) получаем: .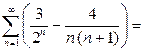

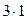
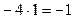Далее мы сосредоточим свое внимание на вопросе о том, как по виду ряда (2) определить, является ли он сходящимся или расходящимся.

Теорема (необходимый признак сходимости ряда). Если ряд 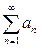сходится, то его общий член стремится к нулю: .

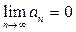Доказательство. Пусть ряд 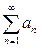сходится, а число 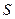является его суммой. Тогда по определению сходящегося ряда предел последовательности его частичных сумм 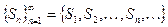равен :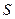

(9) ,

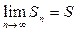где

(10) .

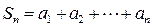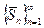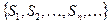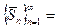
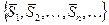
Рассмотрим теперь вспомогательную последовательность , построенную из последовательности добавлением числа 0 в качестве ее первого члена: 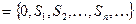. Таким образом, 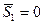, , 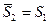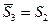и вообще

(11) , .

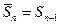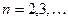Из (11) и (10) следует, что, начиная с :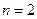

.

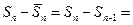
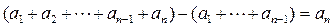Ясно, что такое соотношение выполняется и для 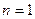: 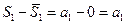. Таким образом, для всех 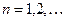выполнено

(12) .

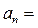
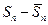Поскольку последовательность чисел 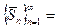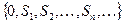, а из (9) последовательность 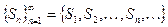имеет пределом число 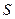, то это же число будет являться и пределом последовательности :

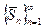(13) .

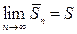Тогда из (12), (9), (13) и свойств пределов вытекает:

= ,

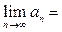
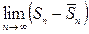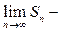
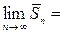
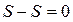что и требовалось доказать.

Из этой теоремы вытекает важное

Следствие (признак расходимости ряда). Если предел 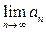общего члена ряда при 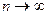либо не существует, либо 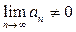, то ряд 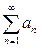расходится.

Таким образом, при выяснении вопроса о сходимости некоторого ряда 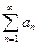следует (если это не сложно) проверить прежде всего выполнение необходимого условия сходимости : 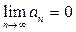. Если оно не выполняется, то сразу можно сказать, что ряд расходится. А вот если выполняется, то без дополнительного исследования ничего о сходимости сказать нельзя и вопрос о сходимости-расходимости остается открытым. Стремление к нулю общего члена ряда является лишь необходимым условием сходимости. Например, гармонический ряд 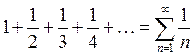оказывается расходящимся, однако нет сомнений в том, что для него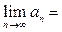 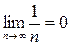. Таким образом, для сходимости ряда нужно, чтобы слагаемые не просто стремились к нулю, а делали бы это «достаточно быстро».

Пример 7. Исследовать сходимость ряда .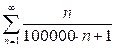

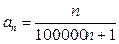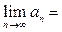
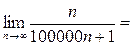
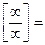
Решение. Общий член этого ряда . Тогда 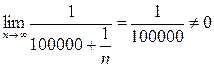. Поэтому по приведенному выше следствию исследуемый ряд расходится.

Большинство признаков сходимости рядов относятся к так называемым положительным рядам (члены которых неотрицательны).

. Поскольку из шолы известна огрессия имеет вид: аjnjhjtncztvsdftncz pyfvtyfntktv 'й последовательности чисо которой (начиная со второго) рав что ряд суммы не имеет . ли имее ф

Положительные ряды

Ряд

(1)

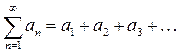
называется положительным, если все его члены неотрицательны: 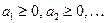. Сначала изучим так называемые признаки сравнения, которые требуют для исследования сходимости данного ряда строить некоторый вспомогательный ряд. Ниже сформулировано соответствующее утверждение, смысл которого достаточно прозрачен.

Теорема (признак сравнения рядов). Пусть имеется два положительных ряда

(2) ,

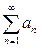(3) ,
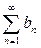причем члены ряда (2) не превосходят соответствующих членов ряда (3):

(4) a_n ≤ b_n

хотя бы начиная с некоторого номера n. Тогда
1) Если сходится ряд с большими членами (3), то сходится и ряд с меньшими членами (2).
2) Если расходится ряд с меньшими членами (2), то расходится и ряд с большими (3).

Рассмотрим примеры применения признака сравнения.
Пример 1. Доказать сходимость ряда

(5) .

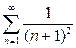Решение. Ряд (5) сравним с рядом 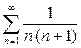, сходимость которого была доказана в предыдущем параграфе. В нашем примере ряд (2) имеет вид исследуемого ряда 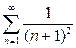(а потому 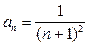), а ряд для сравнения (3) имеет вид 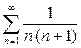(а потому 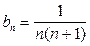). Установим выполнение условия (4) для любого номера n: 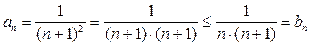. Тогда по первому утверждению признака сравнения рядов исходный ряд (5) сходится.

Основные недостатки при практическом применении приведенного признака сравнения − это

· необходимость правильного подбора вспомогательного ряда, сходимость или расходимость которого известна;

· необходимость доказательства соответствующего неравенства между членами исследуемого и вспомогательного рядов.

Второго из этих недостатков лишен признак сравнения в предельной форме.

Теорема (признак сравнения в предельной форме). Пусть имеются два положительных ряда 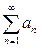и 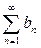(ряды (2) и (3) ), для которых выполняется:

(6) 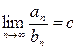, причем и .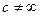

Тогда оба ряда сходятся или расходятся одновременно, т.е. если мы знаем о сходимости или расходимости одного из рядов (например, ряда (3) ), то тот же вывод можно сделать и о втором ряде (ряде (2)) .

Для применения признаков сравнения необходимо иметь так называемые эталонные ряды, про которые известно, сходятся они или расходятся, чтобы сравнивать с ними исследуемые ряды. Чаще всего в качестве таких рядов выступает геометрическая прогрессия, а также ряды вида

(7) ,

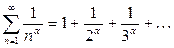про которые известно, что они сходятся при 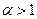и расходятся при 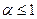(это будет доказано ниже в примере 8). В частности, гармонический ряд 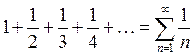расходится (это ряд вида (7) при 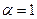). Самый важный этап применения признаков сравнения – это правильный выбор эталонных вспомогательных рядов для сравнения с исследуемым рядом. При этом надо обеспечить либо нужное неравенство между слагаемыми двух рядов, либо обеспечить выполнение условия (6). Например, если мы хотим в качестве ряда сравнения выбрать ряд вида (7), то надо правильно выбрать значение параметра 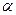в (7), чтобы обеспечить выполнение условия (6). При неправильном выборе значения этого параметра значение 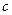этого предела в (6) как раз и оказывается равным либо нулю, либо бесконечности, при которых предельный признак сравнения не работает. Ниже приводится один из возможных приемов выбора правильного значения параметра 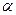при использовании для сравнения эталонного ряда вида (7).

Пример 2. Исследовать сходимость ряда

(8) .

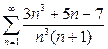Решение. Для ряда (8) подберем для сравнения вспомогательный ряд вида (7) с таким значением параметра 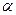, при которым окажется выполненным соотношение (6). В нашем примере ряд (2) есть исследуемый ряд (8), а ряд (3) есть ряд 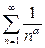, а потому общие члены этих рядов 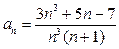, 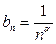. Для выбора подходящего значения параметра 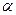оценим поведение 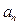, оставляя в числителе и знаменателе только старшие степени 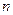, которые и определяют скорости роста числителя и знаменателя с ростом 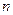. Далее значок ~ можно перевести как «ведет себя так же, как». Итак,

~ .
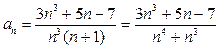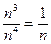