Разложение функций в степенные ряды 4 страница

Следствие. Сумма 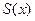степенного ряда (9) является бесконечно дифференцируемой (т.е. имеет производные любого порядка) функцией на интервале сходимости этого ряда .

С помощью приведенной выше теоремы можно находить области сходимости и (что наиболее важно) формулы для сумм некоторых степенных (или числовых) рядов. Для этого с помощью интегрирования или дифференцирования исследуемых рядов получают степенной ряд с известной суммой (например, геометрическую прогрессию), т.е. получают формульное выражение для производной или интеграла от искомой суммы 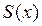. а затем по этому выражению восстанавливают и саму функцию .

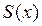Пример 5. Найти интервал сходимости и сумму степенного ряда

(13) .

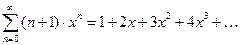Решение. Обозначим через 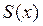сумму этого ряда, пусть 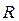− его радиус сходимости. Тогда выполнено: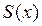 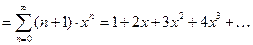для всех точек из интервала сходимости 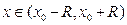. Тогда по формуле (11):

(14) .

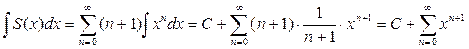Степенной ряд в правой части (14) 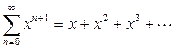при каждом числе 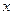представляет собой геометрическую прогрессию с первым членом 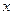и знаменателем прогрессии 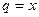. В параграфе «Числовые ряды – основные понятия» мы уже рассматривали условия сходимости геометрической прогрессии и получили, что она сходится только при условии 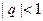. Поэтому областью сходимости ряда 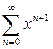является интервал (−1, 1), а для всех 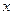из этого интервала сумма ряда (по формуле суммы бесконечной убывающей геометрической прогрессии – формула (6) в параграфе «Числовые ряды – основные понятия») равна 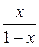. Таким образом, по приведенной выше теореме о почленном дифференцировании и интегрировании степенного ряда интервал сходимости исходного ряда (13) тоже (−1, 1) . Подставляя 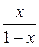в правую часть (14), получаем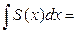 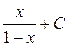. Отсюда следует, что функция 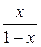является одной из первообразных для 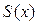, а потому 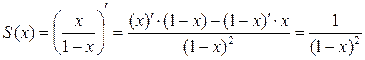. Итак, мы нашли выражение для суммы степенного ряда (13):

(15) , .

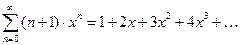
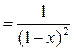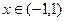Пример 6. Найти сумму числового ряда

(16) .

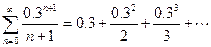Решение. Рассмотрим вспомогательный степенной ряд 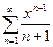, сумму которого обозначим :

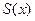(17) .

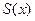
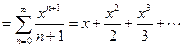Найдем формулу для 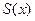, а тогда 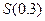даст нам искомую сумму ряда (17). Вычислим производную функции 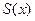в (17), используя формулу (10) почленного дифференцирования ряда:

(18) .

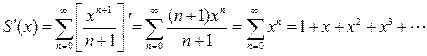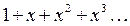
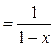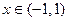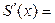
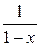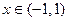Для степенного ряда в правой части (18) мы уже находили сумму и область сходимости (см. параграф «Функциональные ряды», формула (5) ): для всех . Поэтому из (18) получаем, что для . Таким образом, функция 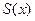оказывается одной из первообразных функции 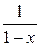. Найдем множество всех первообразных этой функции (т.е. неопределенный интеграл от нее), а затем среди них найдем и 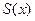: 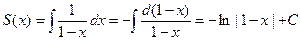. Таким образом, получили, что для :

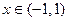(19)

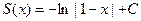
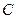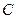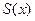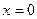при некотором значении произвольной постоянной . Найдем это значение . Из (17) следует, что значение функции при будет 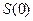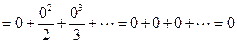. Таким образом,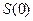 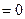, а потому из (19): 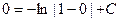, откуда 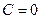. Поэтому из (19) получаем, что 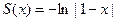для всех 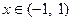. А потому 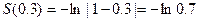. Итак, .

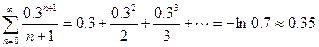Разложение функций в степенные ряды

Используя формулу для суммы бесконечно убывающей геометрической прогрессии, мы в параграфе «Функциональные ряды» (формула (5) ) получили, что сумма степенного ряда 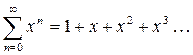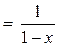для всех 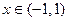. Если теперь поменять местами левую и правую часть этого равенства, то получится, что выполнено равенство

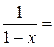
(1) 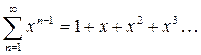для всех .

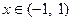Это означает, что функция 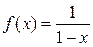представлена на интервале 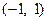в виде сходящегося степенного ряда. А для каких еще функций возможно такое представление? И как его найти?

Введем следующее определение. Будем говорить, что функция 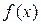разлагается в степенной ряд с центром в 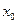на интервале 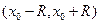, если для всех 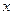из этого интервала справедливо равенство

(2) .

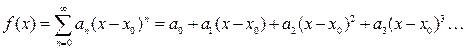Теперь заданные выше вопросы можно переформулировать следующим образом. Какие функции разлагаются в степенные ряды с центром в некоторой точке 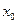и (если разложение возможно) как найти коэффициенты 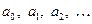этого разложения?

В предыдущем параграфе было сформулировано следствие о том, что сумма степенного ряда является бесконечно дифференцируемой функцией на интервале сходимости ряда. Поэтому разлагаться в степенной ряд могут только функции (да и то не все!), имеющие производные любого порядка. Пусть некоторая функция 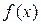имеет производные любого порядка в некоторой окрестности точки 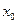. Найдем значения самой функции и всех ее производных (по предположению они существуют!) в этой точке : 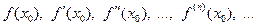. Теперь, используя эти числа, составим следующий степенной ряд:

(3) =

.

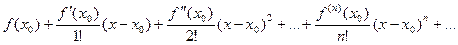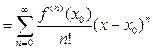Этот ряд называется рядом Тейлора функции 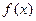с центром в точке 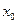. Таким образом, каждой бесконечно дифференцируемой в окрестности точки 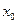функции можно поставить в соответствие некоторый степенной ряд − ее ряд Тейлора. Оказывается, что уж если функция разлагается в окрестности некоторой точки в какой-либо степенной ряд, то этот ряд может быть только рядом Тейлора этой функции. Об этом говорит следующая

Теорема (о единственности разложения в степенной ряд). Пусть функция 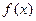разлагается в окрестности точки 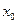в степенной ряд:
(4) .
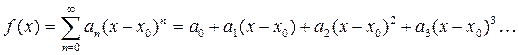Тогда она бесконечно дифференцируема в окрестности этой точки и
(5) .

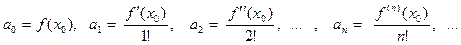Доказательство. Бесконечная дифференцируемость функции 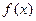, являющейся суммой степенного ряда, уже отмечалась в предыдущем параграфе. Подставив в правую и левую части равенства (4) 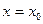, получим первую из формул в (5). Дифференцируя почленно степенной ряд в (4) (а это можно делать с суммой степенного ряда!), получим 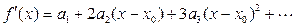. Снова подставляя в это равенство 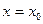, получим вторую из формул в (5). Снова дифференцируя это равенство и подставляя 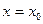, получим третью формулу в (5). И так далее, что завершает доказательство теоремы.

Формулы (5) и дают ответ на вопрос о способе нахождения коэффициентов 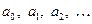разложения функции 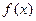в степенной ряд (коли такое разложение вообще возможно). Теперь ответим на вопрос о том, для каких функций гарантирована возможность такого разложения.

Теорема (о разложении). Если функция 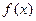бесконечно дифференцируема в некотором интервале 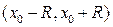и ее производные всех порядков ограничены на этом интервале одним и тем же числом (т.е. в формальной записи 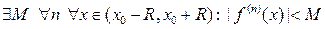), то она разлагается в свой ряд Тейлора на этом интервале, т.е. для всех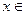 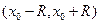имеет место представление:

(6)

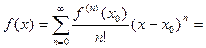
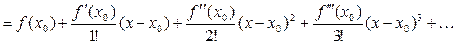
Особенно просто ряд Тейлора (3) для функции 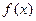выглядит при :

= .

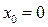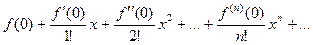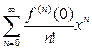В этом случае ряд Тейлора называется рядом Маклорена для функции 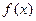. Учитывая (6), находим вид разложения функции в ряд Маклорена ( ):

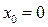(7) .

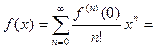
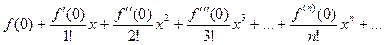Согласно приведенной выше теореме о разложении, представление (7) функции 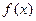в виде ряда Маклорена имеет место на любом интервале вида 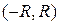, если только функция 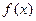бесконечно дифференцируема в интервале 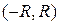и ее производные всех порядков ограничены на этом интервале одним и тем же числом .

Разложение функций в ряд Маклорена применяется значительно чаще, поскольку представляет собой удобное для приложений разложение функции по степеням 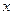(т.е. представляет собой многочлен «бесконечной степени»). Найдем разложения в ряд Маклорена некоторых основных элементарных функций.