Исследование функций и построение графиков
Признак монотонности функции
Одной из существенных характеристик функции является ее поведение на отдельных интервалах — возрастание или убывание. Это определяется приводимой ниже теоремой, доказательство которой мы опускаем.
ТЕОРЕМА 2. Если функция f (x) дифференцируема и f'(x) ≥ 0 (f'(x) ≤ 0) на интервале (а, b), то она не убывает (не возрастает) на этом интервале.
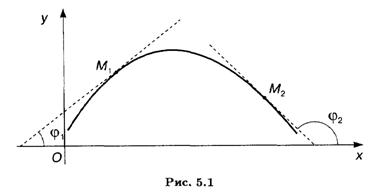
При f'(x) > 0 (f'(x) < 0) имеем признак строгой монотонности, т.е. функция возрастает (убывает). Геометрическая интерпретация связи знака производной функции и характера ее изменения очевидна (рис. 5.1): если углы наклона касательных на каком-то интервале являются острыми, то функция на этом интервале возрастает: tg φ > 0; при тупом угле наклона касательной функция убывает и tg φ < 0.
Точки локального экстремума
Определение 1. Точка x0 называется точкой локального максимума (минимума) функции f(x), если для любого х ≠ x0 в некоторой окрестности точки x0 выполнено неравенство f(x0) > f(х) (f(x0) < f(x)).
Локальный минимум и локальный максимум объединены общим названием локальный экстремум.
ТЕОРЕМА 3 (необходимое условие существования локального экстремума). Если функция f(x) дифференцируема в точке x0 и имеет в этой точке локальный экстремум, то f'(x0) = 0.
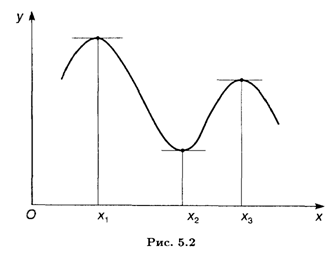
Геометрический смысл теоремы 5.3 указан на рис. 5.2: если в точках локальных экстремумов существуют касательные, то они параллельны оси Ох.
Точки, в которых касательные параллельны оси Оx, а значит, производная равна нулю, называют точками возможного экстремума, или стационарными точками. Если x0 — точка возможного экстремума, т.е. f'(x0) = 0, то она может ине быть точкой локального экстремума. Например, для функции f(x) = x3 (рис. 3.1) производная при х = 0 равна нулю, однако в этой точке нет локального экстремума. Таким образом, теорема 5.3 не является достаточным условием существования локального экстремума.
ТЕОРЕМА 4 (достаточное условие существования локального экстремума). Пусть функция f(x) дифференцируема в некоторой окрестности точки x0. Если при переходе через точку x0 слева направо производная f'(x) меняет знак с плюса на минус (с минуса на плюс), то в точке x0 функция f(x) имеет локальный максимум (минимум). Если же f'(x) не меняет знака в δ-окрестности точки x0, то данная функция не имеет локального экстремума в точке x0.
Рассмотрим применение доказанных теорем на примерах нахождения точек локальных экстремумов функций.
Пример 1. Найти точки локального экстремума и интервалы монотонности функции f(x) = х3 — 7,5x2 + 18x.
Решение. Сначала находим производную f'(x) = 3x2 — 15x + 18. Приравнивая ее к нулю и решая уравнение х2 — 5х + 6 = 0, находим две точки возможного экстремума: x1 = 2 и x2 = 3. Нетрудно видеть, что f'(x) при переходе через точку x1 =2 меняет знак с "+" на "-", т.е. в этой точке имеет место локальный максимум; аналогично устанавливается, что в точке x2 = 3 функция f'(х) имеет локальный минимум.
Найдем теперь интервалы монотонности данной функции (рис. 5.3). Поскольку f'(x) > 0 при х 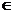 (-
(-  ,2), то в силу теоремы 5.2 функция монотонно возрастает на этом интервале; (2, 3) является интервалом монотонного убывания f(x) (f'(x) < 0), а на интервале (3, +
,2), то в силу теоремы 5.2 функция монотонно возрастает на этом интервале; (2, 3) является интервалом монотонного убывания f(x) (f'(x) < 0), а на интервале (3, +  ) функция монотонно возрастает (f'(x) > 0).
) функция монотонно возрастает (f'(x) > 0).
Пример 2. Найти размеры консервной банки, имеющей форму цилиндра (радиус r и высоту h) заданного объема V, при которых полная поверхность сосуда будет минимальной. Эта задача имеет производственный смысл: найти оптимальные размеры банки, при которых затраты материала на ее изготовление будут минимальны.
Решение. Исходя из формулы объема цилиндра V = πr2h, выразим h:
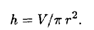
Как известно, полная поверхность цилиндра дается формулой
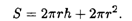
Подставляя сюда формулу для h, получаем S как функцию от r:
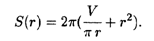
Минимум этой функции найдем из условия S' (r) = 0, откуда получаем уравнение 2r — V / π r2 = 0. Из этого уравнения находим оптимальное значение r; его подставляем в формулу для h и окончательно вычисляем оптимальные размеры банки:
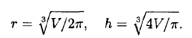
Например, при V = 0,33 л оптимальные размеры банки составят: диаметр дна ≈ 7,5 см и высота ≈ 7,5 см.
Выпуклость и точки перегиба графика функции
Определение 2. Будем говорить, что график функции y = f(x) имеет на интервале (а, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а, b) (рис. 5.4).
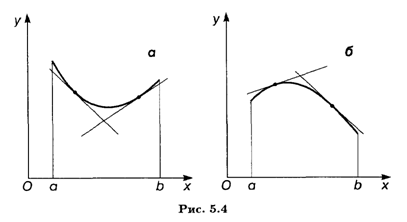
Способ определения направления выпуклости графика функции дается теоремой, приведенной ниже без доказательства.
ТЕОРЕМА 5. Если функция у = f(х) имеет на интервале (а, b) вторую производную и f"(x) ≥ 0 (f"(x) ≤ 0) на (а, b), то график функции имеет на (а, b) выпуклость, направленную вниз (вверх).
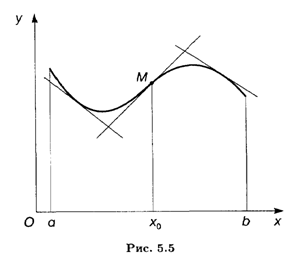
Определение 3. Точка М(x0, f(x0)) называется точкой перегиба графика функции у = f(x), если в точке М график имеет касательную и существует такая окрестность точки x0, в пределах которой график функции f(x) имеет разные направления выпуклости.
В точке перегиба касательная пересекает график функции, поскольку он переходит с одной стороны касательной на другую, т.е. "перегибается" через нее (рис. 5.5).
ТЕОРЕМА 6. (необходимое условие существования точки перегиба). Пусть график функции у = f(x) имеет перегиб в точке M(x0, f(x0)) и функция f(x) имеет в точке x0 непрерывную вторую производную. Тогда

Отметим, что не всегда условие f"(x0) = 0 означает наличие точки перегиба на графике функции у = f(x). Например, график функции у = x2n (п > 1) не имеет перегиба в точке (0, 0), хотя при х = 0 вторая производная равна нулю. Потому равенство (5.8) является только необходимым условием перегиба. Точки графика, для которых условие (5.8) выполнено, будем называть критическими. В каждой такой точке необходимо исследовать дополнительно вопрос о наличии перегиба; здесь имеется полная аналогия с существованием экстремума функции.
ТЕОРЕМА 7 (достаточное условие существования точки перегиба). Пусть в некоторой окрестности точки x0 вторая производная функции у = f(x) имеет разные знаки слева и справа от x0. Тогда график у = f(x) имеет перегиб в точке М(x0, f(x0)).
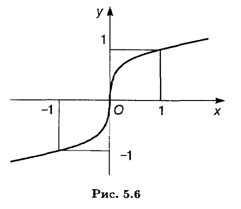
Теорема верна и для случая, когда f"(x) существует в некоторой окрестности точки x0 за исключением самой точки x0 и существует касательная к графику функции в точке М. Например, функция f(x) = x1/3 в точке х = 0 имеет бесконечные производные; в точке O(0, 0) касательная совпадает с осью Оу. Однако график этой функции имеет перегиб в начале координат, поскольку вторая производная f"(x) = -2 /(9x5/3) имеет разные знаки слева и справа от точки х = 0 (рис. 5.6). Рассмотрим примеры: найти точки перегиба и направления выпуклости графиков следующих функций.
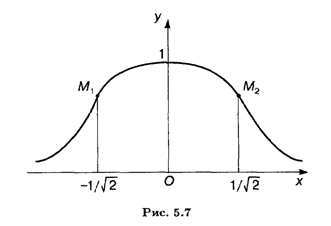
Пример 3. f(x) = ехр (-x2).
Решение. Последовательно находим f'(x)= -2x exp(—x2), f"(x) = 2 exp (-x2)(2x2 — 1). Приравнивая вторую производную к нулю, получаем критические точки х = ±1/ 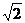 . Ввиду зависимости функции от х2 достаточно исследовать точку x = l/
. Ввиду зависимости функции от х2 достаточно исследовать точку x = l/ 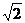 . Нетрудно видеть, что при переходе через эту точку слева направо f"(x) меняет знак с минуса на плюс. Следовательно, на левой ветви функции точка M1(-1 /
. Нетрудно видеть, что при переходе через эту точку слева направо f"(x) меняет знак с минуса на плюс. Следовательно, на левой ветви функции точка M1(-1 / 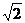 , e-1/2) является точкой перегиба графика функции со сменой выпуклости вниз слева на выпуклость вверх справа (рис. 5.7). На правой ветви в точке перегиба М2(1/
, e-1/2) является точкой перегиба графика функции со сменой выпуклости вниз слева на выпуклость вверх справа (рис. 5.7). На правой ветви в точке перегиба М2(1/ 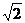 , е-1/2) графика функции имеет место смена выпуклости вверх слева на выпуклость вниз справа.
, е-1/2) графика функции имеет место смена выпуклости вверх слева на выпуклость вниз справа.
Пример 4. f(x) = ln (х2 – 2x + 2).
РHешение. Вторая производная равна 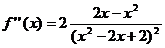 . Приравнивая ее к нулю, получаем критические точки x1 = 0, x2 = 2. Несложный анализ квадратного трехчлена х(2 — х), стоящего в числителе второй производной и определяющего ее знак, показывает, что точка перегиба M1 (0, ln 2) графика функции меняет выпуклость вверх слева на выпуклость вниз справа; в другой точке перегиба М2 (2, ln2) выпуклость графика функции вниз слева меняется на выпуклость вверх справа.
. Приравнивая ее к нулю, получаем критические точки x1 = 0, x2 = 2. Несложный анализ квадратного трехчлена х(2 — х), стоящего в числителе второй производной и определяющего ее знак, показывает, что точка перегиба M1 (0, ln 2) графика функции меняет выпуклость вверх слева на выпуклость вниз справа; в другой точке перегиба М2 (2, ln2) выпуклость графика функции вниз слева меняется на выпуклость вверх справа.
Асимптоты графика функции
Часто оказывается, что график функции неограниченно приближается к некоторой прямой. Такого рода прямые называются асимптотами. Неограниченность приближения графика функции к асимптоте означает, что расстояние от графика до этой прямой (перпендикуляр, опущенный из произвольной точки графика на прямую) стремится к нулю.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 4. Прямая х = а называется вертикальной асимптотой графика функции у = f(x), если хотя бы одно из предельных значений  f(x) или
f(x) или 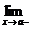 f(x) равно +
f(x) равно +  или -
или -  .
.
Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Например, график функции у = е1/x имеет вертикальную асимптоту х = 0, так как f(x) 
 при х
при х  0+.
0+.
Определение 5. Прямая у = kx + b называется наклонной асимптотой графика функции у = f(x) при х  ±
±  , если f(x) можно представить в виде
, если f(x) можно представить в виде
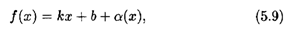
где α(х)  0 при х
0 при х  ±
±  .
.
Это определение относится как к наклонной, так и к горизонтальной асимптотам: в случае горизонтальной асимптоты угловой коэффициент k в (5.9) равен нулю.
Укажем способ нахождения коэффициентов k и b в уравнении наклонной асимптоты. Разделив обе части равенства (5.9) на x и перейдя к пределу при х 
 , получим
, получим
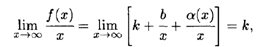
т.е. k = 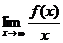 . Затемиз равенства (5.9) находим:
. Затемиз равенства (5.9) находим:
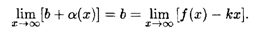
Рассмотрим примеры: найти асимптоты графиков функций.
Пример 5. f(x) = 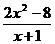 .
.
Решение. Найдем вертикальную асимптоту. Точка x = -1 является точкой разрыва 2-го рода, причем
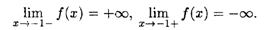
Затем находим наклонные асимптоты:
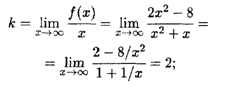
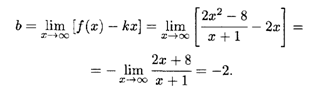
Таким образом, получаем уравнение наклонной асимптоты
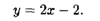
Пример 6. f(x) = х + e-x.
Решение. Вертикальных асимптот здесь нет, поскольку точки разрыва 2-го рода отсутствуют. Отыщем наклонную асимптоту:
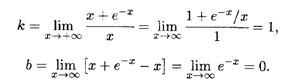
Таким образом, уравнение наклонной асимптоты имеет вид
Схема исследования графика функции
Приведем схему исследования поведения функции и построения ее графика.
1. Найти область определения функции.
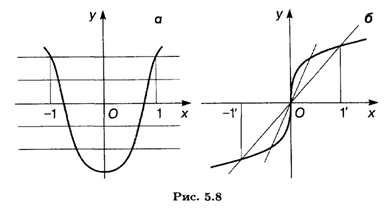
2. Определить возможный тип симметрии функции: четность или нечетность функции. Функция f(x) называется четной, если выполнено условие симметрии ее графика относительно оси Оу:

Функция f(x) называется нечетной, если выполнено условие симметрии ее графика относительно начала координат O (0, 0):

При наличии симметрии достаточно построить график функции на правой координатной полуплоскости и затем отобразить его на левую половину: зеркально относительно оси Оу в случае (5.10) (рис. 5.8,а) или с центральной симметрией в случае (5.11) (рис. 5.8,6).
3. Найти точки пересечения графика функции с осями координат Ох и Оу, т.е. решить соответственно уравнения у = f(0) и f(x) = 0.
4. Найти асимптоты.
5. Найти точки возможного экстремума.
6. Найти критические точки.
7. Исследовать знаки первой и второй производных, определить участки монотонности функции, направление выпуклости графика, точки экстремума и перегиба.
8. Определить максимум и минимум функции на области ее определения. Если областью определения функции является отрезок [а, b], необходимо вычислить значения функции в его концах и сопоставить их с локальными экстремумами.
9. Построить график функции с учетом проведенного исследования.
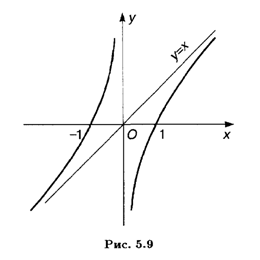
Пример 7. Исследовать и построить график функции

Решение. Действуем по приведенной выше схеме.
1. Область определения функции: х ≠ 0 или х  (-
(-  , 0)
, 0)  (0,
(0,  ).
).
2. Функция (5.12) является нечетной, так как f(-x) = - f(x).
3. Уравнение f(x) = 0 дает корни х = ±1 (точки пересечения с осью Ох). Пересечения с осью Оу нет в силу п.1.
4. Имеется вертикальная асимптота — ось Оу, так как предел f(x) при х  0 бесконечен: f(x)
0 бесконечен: f(x)  +
+  при х
при х  0-, f(x)
0-, f(x)  -
-  при х
при х  0+.
0+.
Определяем наклонную асимптоту:
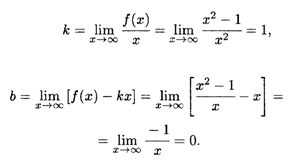
Итак, уравнение наклонной асимптоты: у = х.
5. f'(x) = 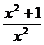 , т.е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде f'(x) положительна.
, т.е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде f'(x) положительна.
6. f"(x) = —2/х3 — критических точек нет.
7. Функция (5.12) монотонно возрастает на всей области своего определения, так как ее производная всюду положительна. В левой координатной полуплоскости выпуклость графика функции направлена вниз (f"(x) > 0), в правой полуплоскости выпуклость направлена вверх (f"(x) < 0).
8. Наибольшего и наименьшего значений функции не существует, поскольку область ее значений неограничена.
9. График функции (5.12) приведен на рис. 5.9.
Применение в экономике
Предельные показатели в микроэкономике
Приведем примеры двух предельных показателей в микроэкономике.
1. Первый из них связан с зависимостью себестоимости С произведенной продукции от ее объема Q: С = f(Q). Так называемая предельная себестоимость характеризует себестоимость ΔC прироста продукции ΔQ:

В предположении о непрерывной зависимости ΔС от ΔQ естественно напрашивается замена разностного отношения в (5.13) его пределом:
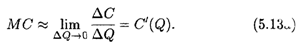
Обычно в приложениях с использованием аппарата математики под предельной себестоимостью понимают именно величину (5.13а).
Например, пусть зависимость издержек производства от объема выпускаемой продукции выражается формулой
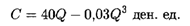
Определим средние и предельные издержки при объеме продукции Q = 15 ден. ед.
А) Функция средних издержек на единицу продукции определяется по формуле 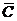 = C/Q, или в нашем случае
= C/Q, или в нашем случае
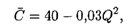
откуда 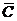 (15) = 40 - 0,03 ∙ 225 = 33,25 ден. ед.
(15) = 40 - 0,03 ∙ 225 = 33,25 ден. ед.
Б) Предельные издержки определяются, согласно (5.13а), по формуле
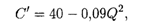
откуда при Q = 15 получаем С' (15) = 19,75 ден. ед.
Иными словами, при средних издержках на производство единицы продукции в 33,25 ден. ед. дополнительные затраты на производство единицы дополнительной продукции составят 19,75 ден. ед. и не превысят средних издержек.
2. В анализе и прогнозах ценовой политики применяется понятие эластичности спроса. Пусть D = f(Р) — функция спроса от цены товара Р (см. п. 3.1). Тогда под эластичностью спроса понимается процентное изменение спроса при изменении цены товара на один процент:
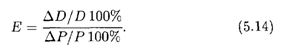
Как и в предыдущем случае, в случае непрерывной зависимости ΔD от ΔQ удобно перейти к пределу при ΔР  0:
0:

Аналогичное понятие можно ввести и для функции предложения S(P). Напомним, что функция D(P) убывает, а функция S(P) возрастает с ростом цены Р.
Укажем некоторые свойства эластичности. Как следует из формулы (5.14а), ее можно выразить так:
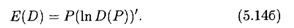
Из равенства (5.14 б) следует, что E(D) обладает свойствами логарифма, а значит,
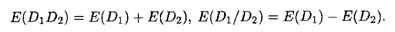
Заметим, что поскольку функция D(P) убывающая, то D'(P) < 0, а тогда согласно формуле (5.14а) и E(D) < 0. Напротив, поскольку функция предложения возрастающая, то соответствующая эластичность E(S) > 0.
Различают три вида спроса в зависимости от величины |E(D)|:
а) если |E(D)| > 1 (E(D) < -1), то спрос считается эластичным;
б) если |E(D)| = 1 (E(D) = -1), то спрос нейтрален;
в) если |E(D)| < 1 (E(D) > -1), то спрос неэластичный.
Рассмотрим два примера из этой области.
Пример 1. Пусть функция спроса описывается формулой
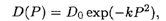
где D0 и k — известные величины. Найти, при каких значениях цены Р спрос будет эластичным.
Решение. Согласно формуле (5.14а) составляем выражение для E(D):
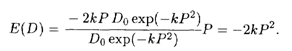
Для того чтобы спрос был эластичным (случай а), необходимо, чтобы выполнялось неравенство
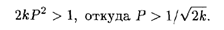
Пример 2. Найти изменение выручки с увеличением цены на товар при разных вариантах эластичности спроса.
Решение. Выручка I равна произведению цены Р на товар на величину спроса D:
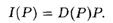
Найдем производную этой функции:
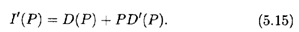
Теперь проанализируем все варианты эластичности спроса, приведенные выше, с учетом формулы (5.14а).
1) E(D) < -1; тогда, подставляя (5.14а) в это неравенство, получаем, что правая часть уравнения (5.15) отрицательна. Таким образом, при эластичном спросе повышение цены Р ведет к снижению выручки. Напротив, снижение цены на товар увеличивает выручку.
2) E(D) = -1. Из (5.14а) следует, что правая часть (5.15) равна нулю, т.е. при нейтральном спросе изменение цены на товар не влияет на выручку.
3) E(D) > -1. Тогда I'(P) > 0, т.е. при неэластичном спросе повышение цены Р на товар приводит к росту выручки.
Понятие эластичности распространяется и на другие области экономики. Рассмотрим один характерный пример.
Пример 3. Пусть зависимость между себестоимостью продукции С и объемом Q ее производства выражается формулой
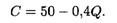
Требуется определить эластичность себестоимости при выпуске продукции Q = 30 ден. ед.
Решение. По формуле (5.14а) получаем
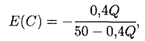
откуда при Q = 30 искомая эластичность составит около —0,32, т.е. при данном объеме выпуска продукции его увеличение на 1% приведет к снижению себестоимости примерно на 0,32%.
Максимизация прибыли
Пусть Q — количество реализованного товара, R(Q) — функция дохода; C(Q) — функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой
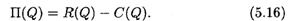
В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с (5.14а), так что этот принцип можно записать в виде R'(Q) = C'(Q). Действительно, из необходимого условия экстремума для функции (5.16) следует, что П'(Q) = 0, откуда и получается основной принцип.
Пример 4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:
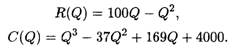
Решение. Согласно (5.16), прибыль П(Q) = - Q3 + 36Q2 - 69Q — 4000. Приравнивая производную функции прибыли к нулю, получаем уравнение
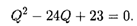
Корни этого уравнения Q1 = 1, Q2 = 23. Проверка показывает, что максимальная прибыль достигается при Q = 23: Пmах = 1290.
Закон убывающей эффективности производства
Этот закон утверждает, что при увеличении одного из основных факторов производства, например капитальных затрат К, прирост производства начиная с некоторого значения К является убывающей функцией. Иными словами, объем произведенной продукции V как функция от К описывается графиком со сменой выпуклости вниз на выпуклость вверх.
Пример 5. Пусть эта функция дается уравнением
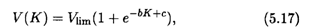
где b и с — известные положительные числа (они определяются прежде всего структурой организации производства), а Vlim — предельно возможный объем выпускаемой продукции. Нетрудно подсчитать, что вторая производная функции (5.17) имеет вид
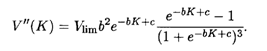
Критическая точка находится из условия V"(K) = 0, откуда

График функции (5.17) приведен на рис. 5.10. В точке перегиба (5.18) выпуклость графика функции вниз меняется на выпуклость вверх. До этой точки увеличение капитальных затрат приводит к интенсивному росту объема продукции: темп прироста объема продукции (аналог первой производной) возрастает, т.е. V"(K) > 0. При К > Кcr темп прироста объема выпускаемой продукции снижается, т.е. V"(K) < 0, и эффективность увеличения капитальных затрат падает.
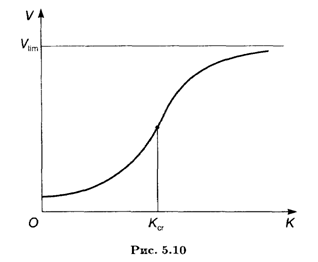
Таким образом, в стратегии капиталовложений оказывается очень важным моментом определение критического объема затрат, сверх которого дополнительные затраты будут приводить все к меньшей отдаче при данной структуре организации производства. Зная этот прогноз, можно пытаться совершенствовать и менять структуру организации производства: "улучшать" показатели b, с и Vlim в сторону повышения эффективности капиталовложений.
УПРАЖНЕНИЯ
Найти пределы с использованием правила Лопиталя.
5.1. 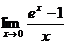 .5.2.
.5.2. 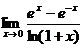 .
.
5.3. 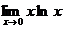 .5.4.
.5.4. 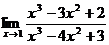 .
.
5.5. 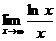 .5.6.
.5.6. 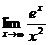 .5.7.
.5.7. 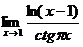 .
.
5.8.  .5.9.
.5.9. 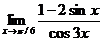 .
.
5.10. 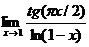 .5.11.
.5.11. 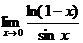 .
.
5.12. Разложить по формуле Маклорена функцию f(x) = tg x до члена с x3 включительно.
5.13. Разложить по формуле Маклорена функцию f(x) = e-x до члена с x2 включительно.
Найти пределы с использованием разложений по формуле Маклорена.
5.14. 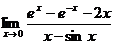 . 5.15.
. 5.15. 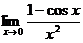 .
.
5.16. 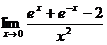 .5.17.
.5.17. 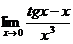 .
.
Найти интервалы выпуклости и точки перегиба графиков функций.
5.18. 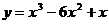 .5.19.
.5.19. 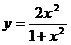
5.20. 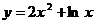 .
.
Найти асимптоты графиков функций.
5.21. 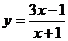 . 5.22.
. 5.22. 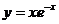 .
.
5.23. 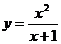 .
.
Исследовать и построить графики функций.
5.24. 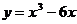 .5.25.
.5.25. 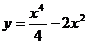 .
.
5.26. 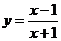 . 5.27.
. 5.27. 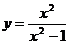 .
.
5.28. 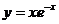 .5.29.
.5.29. 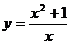 .
.
5.30. 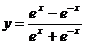 . 5.31.
. 5.31. 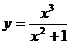
5.32. 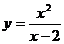 .5.33.
.5.33. 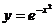 .
.
Решите задачи на наибольшее и наименьшее значения.
5.34. Разложить число 12 на два слагаемых так, чтобы их произведение было наибольшим.
5.35. Определить размеры открытого бассейна с квадратным дном объемом V, при которых на облицовку дна и стен пойдет наименьшее количество материала.
5.36. Даны точки А(0, 3) и В(4, 5). На оси Ох найти точку, сумма расстояний от которой до точек А и В наименьшая.
Решите задачи с экономическим содержанием.
5.37. Зависимость между издержками производства С и объемом продукции Q выражается функцией С = 30Q — 0,08Q3. Определить средние и предельные издержки при объеме продукции: а) Q = 5 ед., б) Q = 10 ед.
5.38. Функции долговременного спроса D и предложения S от цены р на мировом рынке нефти имеют соответственно вид
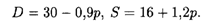
1) Найти эластичность спроса в точке равновесной цены.
2) Как изменятся равновесная цена и эластичность спроса при уменьшении предложения нефти на рынке на 25%?
5.39. Функции спроса D и предложения S от цены р выражаются соответственно уравнениями
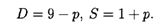
Найти эластичность спроса и предложения при равновесной цене, а также изменение дохода (в процентах) при увеличении цены на 10%.
5.40. Зависимость объема выпуска продукции V от капитальных затрат К определяется функцией V = V0 ln (4 + K3). Найти интервал изменения К, на котором увеличение капитальных затрат неэффективно.
