Наибольшее и наименьшее значение функции на отрезке
Пусть функция 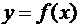 непрерывна на отрезке [a,b]. Тогда на этом отрезке функция достигает наибольшего и наименьшего значений (2-ая теорема Вейерштрасса). Остановимся для определенности на наибольшем значении.
непрерывна на отрезке [a,b]. Тогда на этом отрезке функция достигает наибольшего и наименьшего значений (2-ая теорема Вейерштрасса). Остановимся для определенности на наибольшем значении.
Если оно достигается в некоторой точке между a и b, то это одновременно будет одним из максимумов (очевидно, наибольшим); но наибольшее значение может достигается и на одном из концов промежутка, a или b.
Итак, функция на отрезке [a,b] достигает своего наибольшего значения либо на одном из концов этого отрезка, либо в такой внутренней точке этого отрезка, которая является точкой максимума.
То же самое можно сказать и о наименьшем значении функции: оно достигается либо на одном из концов данного отрезка, либо в такой внутренней точке, которая является точкой минимума.
Из предыдущего вытекает следующее правило: если требуется найти наибольшее значение непрерывной функции на промежутке [a,b], то надо:
1) найти все максимумы функции на отрезке;
2) определить значения функции f(a) и f(b) на концах отрезка;
3) из всех полученных выше значений функции выбрать наибольшее; оно и будет представлять собой наибольшее значение функции на отрезке.
Аналогичным образом следует поступать и при определении наименьшего значения функции на отрезке.
С помощью теории максимума и минимума решаются многие задачи геометрии, физики и т.д. Рассмотрим некоторые из таких задач.
Задача 1. Затраты на перевозку груза по железной дороге в единицу времени состоят из двух частей: постоянной, равной a, и переменной, пропорциональной v3, где v – скорость. При какой скорости затраты на перевозку груза будут наименьшими?
Решение. Обозначим расходы на перевозку груза в единицу времени через q. Тогда q = a + bv3, где b – коэффициент пропорциональности.
Затраты на перевозку грузу составляют
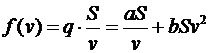 ,
,
где S – расстояние, на которое перевозится груз.
Затраты на перевозку необходимо выбрать наименьшими. Для этого нужно исследовать функцию
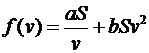
на минимум. Находим

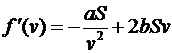 ,
, 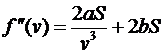 ,
,
откуда
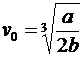 ,
, 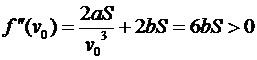 , так как b > 0 и S > 0.
, так как b > 0 и S > 0.
При этой скорости движения затраты будут наименьшими так как при v → 0 и v → ∞ затраты неограниченно возрастают.
Задача 2. Дальность S полета снаряда, выпущенного с начальной скоростью v0из орудия, наклоненного под углом φ к горизонту, определяется формулой
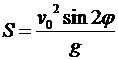 ,
,
где g – ускорение свободного падения. Определить угол φ0, при котором дальность S будет наибольшей при данной начальной скорости v0.
Решение. Величина S представляет собой функцию переменного угла φ. Исследуем эту функцию на максимум на отрезке 0 £ φ £ 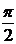 :
:
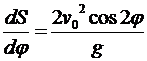 ,
, 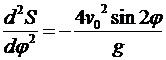
откуда
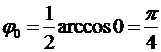 ,
, 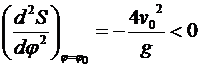
следовательно, при значении φ = 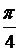 дальность полета S имеет максимум
дальность полета S имеет максимум
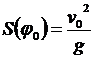 .
.
Значения функции S(φ) на концах отрезка [0, 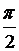 ] равны:
] равны:
S(0) = 0, S( 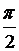 ) = 0.
) = 0.
Таким образом, найденный максимум и есть искомое наибольшее значение S.
Асимптоты
Очень часто приходится исследовать форму кривой y = f(x), а значит, и характер изменения соответствующей функции при неограниченном возрастании (по абсолютной величине) абсциссы x или ординаты y переменной точки М(x,y) кривой или абсциссы и ординаты одновременно. При этом важным частным случаем является тот, когда исследуемая кривая при удалении ее переменной точки М(x,y) в бесконечность (расстояние этой точки от начала координат неограниченно возрастает) неограниченно приближается к некоторой прямой.
Определение. Если рассеяние δ от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой (рис.26).
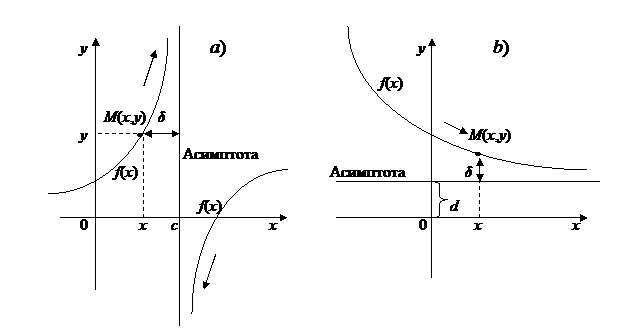
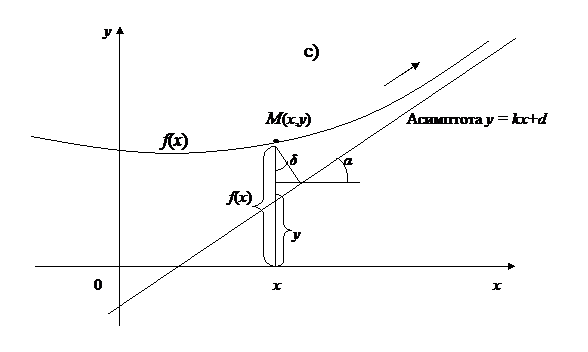
Рис. 26
Кривые с бесконечной ветвью могут иметь три вида асимптот: вертикальные (т.е. параллельные оси ординат, рис.26,а), горизонтальные (т.е. параллельные оси абсцисс, рис.26,b) и наклонные (рис.26,с).
Вертикальные асимптоты
Из определения асимптот следует, что если 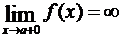 , или
, или 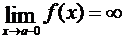 , или
, или 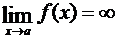 , то прямая x = a есть асимптота кривой y = f(x); и обратно, если прямая x = a есть асимптота, то выполняется одно из написанных равенств.
, то прямая x = a есть асимптота кривой y = f(x); и обратно, если прямая x = a есть асимптота, то выполняется одно из написанных равенств.
Следовательно, для отыскания вертикальных асимптот нужно найти такие значения x = a, при приближении к которым функция 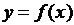 стремится к бесконечности. Тогда прямая x = a будет вертикальной асимптотой. Точкам x = a соответствуют разрывы функции f(x) второго рода. Например, кривая
стремится к бесконечности. Тогда прямая x = a будет вертикальной асимптотой. Точкам x = a соответствуют разрывы функции f(x) второго рода. Например, кривая 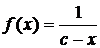 имеет вертикальную асимптоту x = с, так как
имеет вертикальную асимптоту x = с, так как 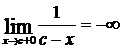 ;
; 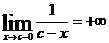 (или
(или 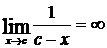 ).
).
В точке x = с функция 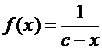 терпит разрыв второго рода (рис.26,а).
терпит разрыв второго рода (рис.26,а).
Горизонтальные асимптоты
Для того чтобы, например, при x → +∞, прямая y = d служила асимптотой для кривой f(x), очевидно (рис.26,b), необходимо и достаточно, чтобы было
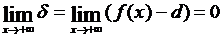 или
или 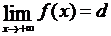 .
.
Таким образом, вопрос о горизонтальной асимптоте сводится попросту к вопросу об этом пределе.
Отдельно нужно искать подобный предел и при x → –∞; при этом может получиться и другая асимптота. Например, в случае кривой f(x) = arctg x (рис.8) имеем: 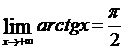 ;
; 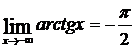 .
.
Следовательно, для кривой f(x) = arctg x,при x → +∞ асимптотой является прямая 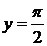 , а при x → –∞ – прямая
, а при x → –∞ – прямая 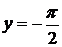 (рис.8).
(рис.8).
Наклонные асимптоты
Предположим, что кривая f(x) имеет наклонную асимптоту y = kx+d, например, со стороны положительной части оси Oх (рис.26,c). Определим числа k и d. Так как разность ординат 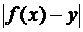 лишь постоянным множителем (равным косинусу угла между асимптотой и осью Oх) разнится от расстояния δ (
лишь постоянным множителем (равным косинусу угла между асимптотой и осью Oх) разнится от расстояния δ ( 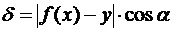 , рис.26,с), то при x → +∞ одновременно с δ должна стремится к нулю и эта разность.
, рис.26,с), то при x → +∞ одновременно с δ должна стремится к нулю и эта разность.
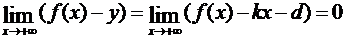 . (3.71)
. (3.71)
Разделив на x, получим отсюда:
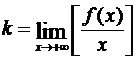 (так как
(так как 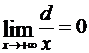 ). (3.72)
). (3.72)
Зная k, из равенства (3.71) находим d:
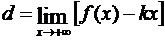 . (3.73)
. (3.73)
Итак, для того чтобы прямая y = kx + d была асимптотой для данной кривой, необходимо выполнение условий (3.72) и (3.73). Обратное рассуждение покажет и их достаточность. Вопрос здесь сведется к последовательному разысканию пределов (3.72) и (3.73), которыми уже и определятся коэффициенты уравнения прямой y = kx + d, удовлетворяющей равенству (3.71) и, следовательно, обладающей свойством асимптоты.
Мы проводили исследования при x → +∞, но все рассуждения справедливы и при x → –∞. Поэтому для случая x → –∞ нужно повторить все исследование. При этом может получиться и другая асимптота по сравнению со случаем x → +∞. Например, в случае функции 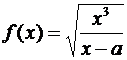 имеем при x → +∞
имеем при x → +∞
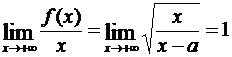 ,
,
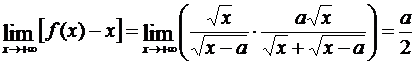 ,
,
так что, со стороны положительных значений x, кривая приближается к асимптоте 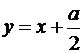 . Со стороны же отрицательных x получается другая асимптота
. Со стороны же отрицательных x получается другая асимптота 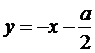 . Действительно, при x → –∞ имеем
. Действительно, при x → –∞ имеем
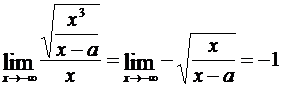 ,
,

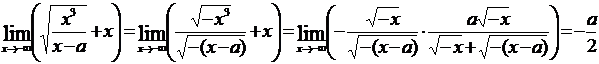 .
.
