Схема исследования функции и построения графика
Для исследования функции y = f(x) и построения ее графика методом дифференциального исчисления целесообразно придерживаться следующей схемы:
1) Определить область D задания функции;
2) Проверить является ли функция четной, нечетной, периодической;
3) Установить точки разрыва функции и выяснить их характер исследованием односторонних пределов функции в данных точках. Для точек в которых функция обращается в бесконечность (точки разрыва второго рода) построить соответствующие вертикальные асимптоты;
4) Найти горизонтальную или наклонную асимптоты графика (и притом отдельно при x → +∞ и при x → –∞, если область D определения функции бесконечна в обе стороны);
5) Определить значения аргумента x 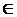 D, для которых производная
D, для которых производная 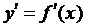 обращается либо в нуль, либо в бесконечность, либо вовсе не существует (т.е. найти критические точки) и подвергнуть их исследованию на зкстремум;
обращается либо в нуль, либо в бесконечность, либо вовсе не существует (т.е. найти критические точки) и подвергнуть их исследованию на зкстремум;
6) Выяснить промежутки монотонности функции. Результаты удобно разложить в таблицы (см. ниже пример);
7) Определить значения x 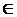 D, для которых вторая производная
D, для которых вторая производная 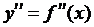 равна нулю, и подвергнуть их исследованию на перегиб;
равна нулю, и подвергнуть их исследованию на перегиб;
8) Выяснить промежутки сохранения направления выпуклости (вверх или вниз) графика функции. Результаты удобно разложить в виде таблицы.
9) Определить значение самой функции y = f(x), отвечающие значениям x 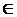 D для пунктов 3), 5), 7), а также на концах рассматриваемой области D. Результаты удобно разложить в виде таблицы (см. ниже пример) с указанием особенности вычисляемой точки графика:
D для пунктов 3), 5), 7), а также на концах рассматриваемой области D. Результаты удобно разложить в виде таблицы (см. ниже пример) с указанием особенности вычисляемой точки графика: 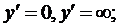 максимум; минимум; перегиб и др. К названным точкам графика при необходимости присоединяют еще и некоторые другие, например, точки пересечения графика с осями.
максимум; минимум; перегиб и др. К названным точкам графика при необходимости присоединяют еще и некоторые другие, например, точки пересечения графика с осями.
10) После нанесения на чертеж всех вычисленных точек пункта 9) через них проводят самый график, учитывая при этом все их особенности и вышеперечисленные пункты.
При исследовании конкретной функции отдельные этапы этой схемы могут быть расширены, другие же могут оказаться излишними или невыполнимыми. Например, вычисление тех значений х,при которых значение функции обращается в нуль.
Пример. Провести исследование и построить график функции
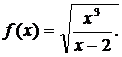
Будем следовать изложенной выше схеме.
1) Функция f(x) получает вещественное значение, лишь если х ≤ 0 или х > 2 и следовательно, D= (–∞, 0] U (2, +∞ );
2) Функция f(x) не является четной, нечетной и периодической;
3) Функция f(x) относится к классу элементарных и поэтому она непрерывна во всей области своего определения. Поэтому исследуем функцию на непрерывность в граничных точках области определения: а) так как 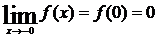 , следовательно, функция f(x) в точке х = 0 непрерывна слева, б) так как
, следовательно, функция f(x) в точке х = 0 непрерывна слева, б) так как 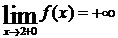 , следовательно, справа от точки х = 2 функция f(x) имеет разрыв второго рода, а график функции имеет вертикальную асимптоту х = 2;
, следовательно, справа от точки х = 2 функция f(x) имеет разрыв второго рода, а график функции имеет вертикальную асимптоту х = 2;
4) Выясним вопрос о существовании горизонтальной или наклонной асимптоты. При х 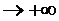
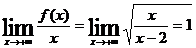 ,
,
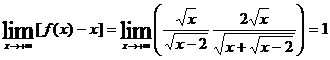 .
.
Отсюда вытекает, что со стороны положительных х, кривая приближается к асимптоте у = х + 1. Аналогично получается со стороны отрицательных х другая асимптота у = –х – 1:
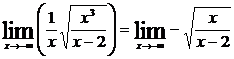 =–1; (см. п.8.4.3);
=–1; (см. п.8.4.3);
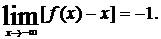
5) Функция f(x) имеет только одну критическую точку х = 3, в ней производная обращается в нуль: 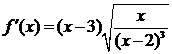 . Знак производной в точке х = 3 меняется с минимума на плюс, следовательно, в данной точке – минимум. Производная
. Знак производной в точке х = 3 меняется с минимума на плюс, следовательно, в данной точке – минимум. Производная 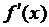 обращается в нуль и при х = 0, но это – конец промежутка (–∞, 0] в котором мы функцию рассматриваем, и об экстремуме здесь не может быть и речи;
обращается в нуль и при х = 0, но это – конец промежутка (–∞, 0] в котором мы функцию рассматриваем, и об экстремуме здесь не может быть и речи;
6) Производная 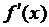 имеет следующие области сохранения знака:
имеет следующие области сохранения знака:
| Область значений х | -∞ <x < 0 | 2 < x <3 | 3 < x < +∞ |
| Знак f′′(x) | минус | минус | плюс |
| Поведение функции | Монотонно убывает | Монотонно убывает | Монотонно возрастает |
7) Вторая производная 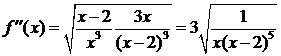 не обращается в нуль ни в одной точке области определения функции и, следовательно, график функции не имеет точек перегиба;
не обращается в нуль ни в одной точке области определения функции и, следовательно, график функции не имеет точек перегиба;
8) Вторая производная больше нуля и при x < 0 и при x > 2, так что кривая обращена вогнотостью всегда вверх;
9) Вычислим значение функции для х = 3 (минимум) и х = 0 (граница области определения функции): f (3) ≈ 5,2; f (0) = 0;
| Значение х | ||
| Значение f(х) | 5,2 | |
Значение 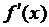 | ||
| Особенности | Граница области определения | минимум |
10) Теперь имеем достаточно данных для построения графика функции (рис.27).
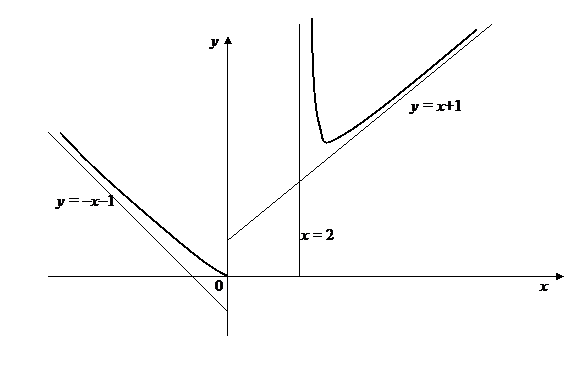
Рис. 27
УПРАЖНЕНИЯ
1. Найти производные следующих функций:
а) 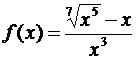 ; б)
; б) 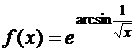 ; в)
; в) 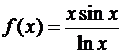 ;
;
г) 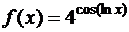 ; д)
; д) 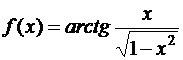 ; е)
; е) 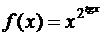 ;
;
ж) 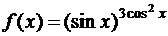 .
.
2. Найти производные следующих функций, заданных неявно:
а) 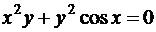 ; б)
; б) 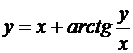 ; в)
; в) 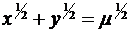 ,
,  .
.
3. Найти уравнение касательной и нормали к кривым второго порядка, проходящих через точку М0 (x0, y0) и лежащую на этих кривых:
а) 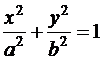 – эллипс; б)
– эллипс; б) 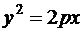 – парабола.
– парабола.
4. Найти производные 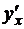 следующих функций, заданных параметрически:
следующих функций, заданных параметрически:
а) 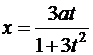 ,
, 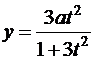 ; б)
; б) 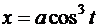 ,
, 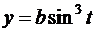 ;
;
в) 
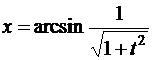 ,
, 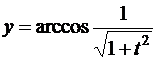 .
.
5. Проверить выполнение условий теоремы Лагранжа (частный случай Ролля) для функций:
а) 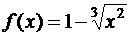 , на отрезке [–1,1]; б)
, на отрезке [–1,1]; б) 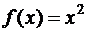 , xÎ[0,1];
, xÎ[0,1];
в) 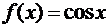 ,
, 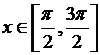 и xÎ[0, π].
и xÎ[0, π].
Если функция удовлетворяет условиям теоремы, найти промежуточное значение ξ.
6. Пользуясь правилом Лопиталя вычислить следующие пределы:
а) 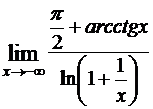 ; б)
; б) 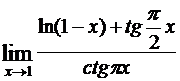 ; в)
; в) 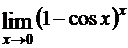 ;
;
г) 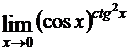 ; д)
; д) 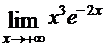 .
.
7. Используя формулу Тейлора вычислить с точностью до 0.001 следующие значения:
а) 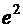 ; б)
; б) 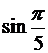 ; в)
; в) 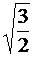 ; г)
; г) 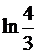 .
.
8. Найти наибольшее и наименьшее значения функций:
а) 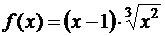 ,
, 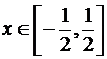 ; б)
; б) 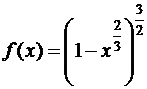 ,
, 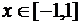 ;
;
в) 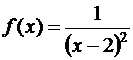 ,
, 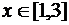 .
.
9. Определить наибольшую площадь равнобедренного треугольника, если: а) боковая сторона треугольника равна μ; б) треугольник вписан в круг радиуса R.
10. Построить графики следующих функций:
а) 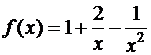 ; б)
; б) 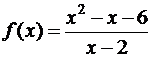 ; в)
; в) 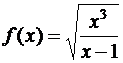 .
.
