Числовые последовательности. Предел последовательности. Предел функции.
Числовые последовательности. Предел последовательности. Предел функции.
Определение: Числовой последовательностью назыв множество чисел, пронумерованных с помощью натуральных чисел и расположенных в порядке возрастания их номеров.
у1, у2, …, уn={yn}→yn=f(n), где у1, у2 –члены, yn=f(n) –общий член последов.
Определение: Число а назыв пределом последов, если 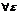 >0, сколь угодно малого
>0, сколь угодно малого 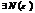 , что для всех n> N(
, что для всех n> N( 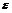 ), выполняется
), выполняется 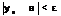 , при этом
, при этом
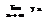 =a, (a-ε;a+ε) - окрестность
=a, (a-ε;a+ε) - окрестность
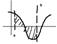
Геометрическая интерпретация
y=f(x) – ф-ция, х - аргумент ф-ции, х→а, f(x) →А, А предел ф-ции
Определение: числа А назыв. пределом ф-ции f(x) при х→а, если 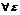 >0, сколь угодно малого,
>0, сколь угодно малого, 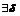 >0, что для всех x, для которых выполняется условие
>0, что для всех x, для которых выполняется условие 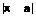 <
< 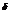 , имеет место
, имеет место 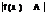 <
< 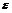
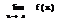 =A
=A
Замечание: 1) х→а как угодно; 2) f(x) в точке а может быть и не определена.
Определение: числа А назыв. пределом ф-ции f(x) при х→∞, если 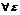 >0, сколь угодно малого,
>0, сколь угодно малого, 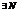 , что для всех x,|x|>N , выполняется.
, что для всех x,|x|>N , выполняется. 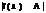 <
< 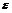
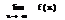 =A
=A
Теорема: Любая функция, имеющая предел, является ограниченной.
Бесконечно малые и бесконечно большие. Теоремы о бесконечно малых.
Определение: Ф-цияf(x) назыв бесконечно малой, если её предел при х→а, равен 0
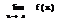 =0
=0
или 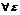 >0,
>0, 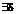 >0. что
>0. что 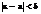 →
→
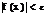
Свойства:
1) 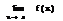 =Аó(f(x) - A) – б.м. при х→а. Следствие
=Аó(f(x) - A) – б.м. при х→а. Следствие 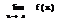 =А → f(x)=A+α, α -б.м.
=А → f(x)=A+α, α -б.м.
2) α, β -б.м. → α + β= б.м.
3) α -б.м. , у- ограниченная, α *у – б.м. Следствие: -
α*β- б.м., где α и β -б.м.
- С* α -б.м, где α -б.м. С - const
4) α/y –б.м. где α-б.м. , lim y≠0
Определение: Ф-цияf(x) назыв бесконечно большой, если её предел при х→а, равен ∞
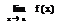 =∞
=∞
Теорема: (связь между б.м и б.б.)
у=f(x) – б.м. при х→а ó 1/f(x) – б.б. при х→а и наоборот.
Теоремы о пределах. Односторонние пределы.
Теорема 1: Пусть lim{x→a}f(x)=А и lim{x→a}g(x)=В, тогда 1)lim{x→a}(f(x)+g(x)) = А+В; 2)lim{x→a}(f(x)*g(x)) = А*В; 3)lim{x→a}(f(x)/g(x)) =А/В
Теорема 2: lim f1(x)= А1 lim f2(x) = А2, f1(x)<=f2(x), 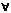 x
x 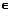 D(f) => A1<A2
D(f) => A1<A2
Теорема 3: lim f1(x)=А, lim f2(x) = А, f1(x)<f(x)<f2(x) => lim f(x) =A
Определение: если при вычислении предела lim{x→a}f(x) при х→а, Х остаётся всё время меньше (больше) а, то предел называется левым(правым) – оба односторонние.
Замечание: 1) Если сущ-ют и равны м/у собой односторонние пределы, то они равны пределу f(x), при х→а. 2) Если существует предел данной функции, то существует и его односторонние пределы.
Первый и второй замечательные пределы.
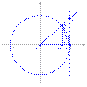
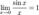 Первый замечательный предел
Первый замечательный предел
Доказательство
Рассмотрим односторонние пределы  и
и 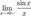 и докажем, что они равны 1.
и докажем, что они равны 1.
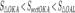 Пусть
Пусть 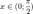 . Отложим этот угол на единичной окружности (R = 1).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.Очевидно, что:
. Отложим этот угол на единичной окружности (R = 1).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.Очевидно, что:
(1)
(где SsectOKA — площадь сектора OKA)
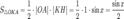
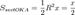
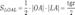
(из 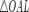 : | LA | = tgx)
: | LA | = tgx)
Подставляя в (1), получим:
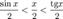
Так как при 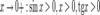 :
:
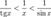
Умножаем на sinx:
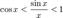
Перейдём к пределу:
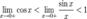
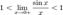
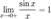
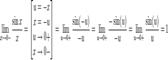 Найдём левый односторонний предел:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
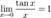
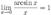
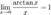

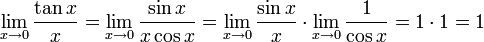
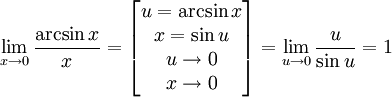
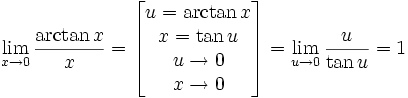
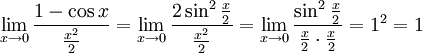
Второй замечательный предел
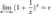
Доказательство второго замечательного предела:
Доказательство второго замечательного предела для случая последовательности (т.е. для натуральных значений x)
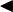 Докажем вначале теорему для случая последовательности
Докажем вначале теорему для случая последовательности 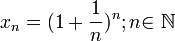
По формуле бинома Ньютона: 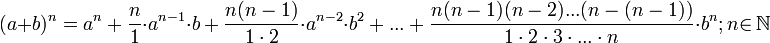
Полагая 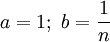 , получим:
, получим:
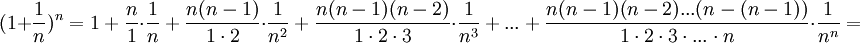
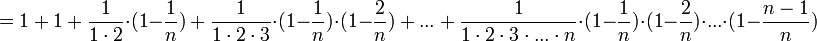 (1)
(1)
Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число  убывет, поэтому величины
убывет, поэтому величины 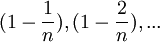 возрастают. Поэтому последовательность
возрастают. Поэтому последовательность 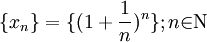 — возрастающая, при этом
— возрастающая, при этом
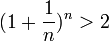 (2).
(2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
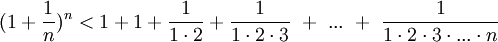
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
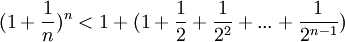 .
.
Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:
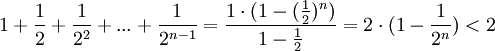 .
.
Поэтому 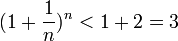 (3).
(3).
Итак, последовательность ограничена сверху, при этом 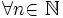 выполняются неравенства (2) и (3):
выполняются неравенства (2) и (3): 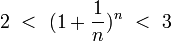 .
.
Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность 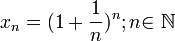 монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.
монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е. 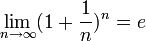

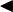 Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, т.е. докажем, что
Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, т.е. докажем, что 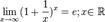 . Рассмотрим два случая:
. Рассмотрим два случая:
1. Пусть 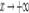 . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами: 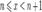 , где n = [x] - это целая часть x.
, где n = [x] - это целая часть x.
Отсюда следует: 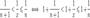 , поэтому
, поэтому
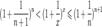 .
.
Если 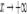 , то
, то 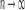 . Поэтому, согласно пределу
. Поэтому, согласно пределу 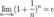 , имеем:
, имеем:

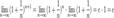 .
.
По признаку (о пределе промежуточной функции) существования пределов 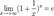 .
.
2. Пусть 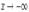 . Сделаем подстановку − x = t, тогда
. Сделаем подстановку − x = t, тогда
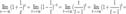
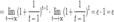 .
.
Из двух этих случаев вытекает, что 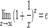 для любого x.
для любого x.
Точки разрыва.
Если для y=f(x) рав-во (3): f(x0 -0)+f(x0 +0) =f(x0) нарушается, то х0 - точка разрыва
Характер нарушения рав-ва (3) кладется в основу классификации точек разрыва:
1. а) если f(x0 -0) и f(x0 +0) сущ-ют и f(x0 -0) ≠f(x0 +0), то х0 - наз. т-кой разрыва 1-го рода с конечным скачком.
Разность f(x0 -0)-f(x0 +0) наз скачком ф-ции в т.х0 b)Если в т. х f(x0 -0) = f(x0 +0) ≠f(x0 ), то х0 наз т-кой разрыва 1 рода устранимой.
2. Если хотя бы один из пределов f(x 0-0) или f(x0 +0) не сущ-ет или =∞, то х0 наз т-кой разрыва 2-го рода ф-ции y=f(x)
Теоремы о непрерывных ф-ях.
Т 1. Если y=f(x) и y=g(x) непрерывны в т. x 0 , то в этой т-ке непрерывны также f(x) ±g(x), f(x)*g(x), f(x)/g(x),(g(x0) ≠0)
Т 2. Сложная ф-ция, составленная из конечного числа непрерывных ф-ций непрерывна.
Т 3. Ф-я обратная к непрерывной и монотонной ф-ции непрерывна.
Вывод: Все элементарные ф-ции непрерывны в областях, где они определены
Геометрический смысл
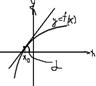
f(x )=tg – угловой коэффициент касательной
Следствия.
1)(cu)'=cu', где с=const
2) (u*v*w)=u'vw+v'uw+w'uv
Ур.кас-ой. нормали.
Касательная - предельное положение секущей.
Нормаль-прямая, перпендик. касательной в точке. Геом.смысл производной
f’(x)=tgA=K
Из аналит.геом
Ур.кос:y-y0=f’(x0)(x-x0) K=-1/f’(x0)
Ур.нормали y-y0=-(x-x0)/f’(x0)
Дифференциал функции
У=f(x) - диф-ма. т. е. сущ-т f’(x)=Lim(Δx→0)ΔY/ΔX
В силу основной теоремы о пределах имеем:
Δy/Δx=f ’(x)+α(Δx) (α(Δx)→0 когда Δx→0)
Δy=f’(x)Δx+ α(Δx)Δx
f’(x)Δx-гл.часть приращения Δy наз-ся диф-ом функции. dy=f ’(x) Δx
Если у=х то dx=Δx dy=f ’(x)dx
Δy=dy+ αΔx
Δy≈dy f’(x)=dy/dx
f(x)-f(x0) ≈ f ’(x0)Δx
f(x) ≈ f(x0)+f’(x0)Δx
геометрич. смысл
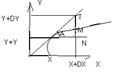 tg(α)=f’(x)
tg(α)=f’(x)
TN=tgαΔx=f ’(x)dx=dy, MN = Δy
{на графике ВМЕСТО X+DX надо писать X+ΔX!}
Т.о.диф-л ф-ии y=f(x) в т.Х есть приращение ординаты касательной приведенный к графику ф-ии y=f(x) в точке (x;f(x))
Св-ва диф-ов: d(u+v)=du+dv
d(uv)=udv+vdu
d(u/v)=(vdu-udv)/v²
Диф-ы высших порядков
Рассм. дифференциал функции:
dy=f ‘(x)dx. Опр. Диф-лом (n)-го порядка наз. дифференциал от дифференциала (n-1)-го порядка
d(d(n-1)y)=d(n)y
d2y=d(dy)=d(f’(x)dx)=(f’(x)dx)’dx=f’’(x)dx2
Диф-ал n-го порядка равен:
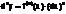
Диф-ы сложных ф-ий
Расм. Сложную ф-ию
{y=f(u),u=g(x)}
Y=f(g(x))=F(x)
dy=F’(x)dx=f’
(u)g’(x)dx=f’(u)du
Св.инвариантности: диф-л 1-го порядка сохр. свою форму независимо от того будет ли аргумент ф-ии независимой переменной или функцией.
Для диф-в высшего порядка это св-во не сохраняется
Правило Лопиталя
используется для нахождения пределов отношений вида 0/0 ∞/∞
Limf(x)/g(x)= f(a)/g(a)=0/0-?;
Limf(x)/g(x)= ∞/∞-?
Т1. Пусть заданы дифференцируемые ф-ии f(x) и g(x) на отрезке [а;b] и f(a)=g(a)=0,то при существовании предела Lim(f(x)/g(x))= Lim(f’(x)/g’(x))
Предел отношения ф-ии равен пределу отношения их производных.
Д-во: т.к. ф-ии диф-емы то к ним применим теорему Коши
f(a)=g(a)=0
[f(x)-f(a)]/[g(x)-g(a)]=f’(ξ)/g’(ξ), →сущ-т т.a<ξ<x если x→a то ξ→a. расм.
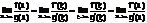
Монотонность ( возр и убыв ф-ии) теорема:
Пусть y=f(x) диф-ма на[ab] тогда если f’(x)>0 то функция возрастает, иначе - убывает
правилo:
1D(x)? 2.f’(x)?
3.f’(x)=0 (находим корни)?
4. Смотрим где че убывает/возрастает
5. Пишем ответ ответ.
Дост. признак экстремума
Пусть т. Х0-критическая (f’(x0)=0, несущ.) если
Правило нахождения экстремума
1. D(x)? 2.f’(x)?
3. крит точки?
4. разбить D(f) точками (+-)
5. Ответ
Дост. признак экстремума
Пустьf’(x0)=0, f’’(x0)≠0 то если f’’(x0)<0 то x0-т.max, f’’(x0)>0 то x0-т.min
Вертикальные асимптоты
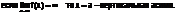 -
-
Наклонная асимптота
Прямая y=kx+b-накл.ассимп графика ф-ии y=f(x) если
f(x)-kx-b→0, т. к. по формуле нахождения расстояния от точки то графика
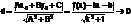
Теорема
Для того чтоб прямая y=kx+b была наклон асимп.грфика ф-ии y=(x) необходимо и достаточно чтобы 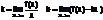
Горизонтальная
Если при нахождении накл.ас. к=0 то y=b- г.о.
28 Первообразная, неопределенный интеграл, его свойства, таблица интегралов.
Ф-ция F(x) называется первообразной для f(x) на некотором интервале. F’(x)=f(x)
Теорема. Если ф-ция f(x) имеет хотя бы одну первообразную F(x),то ф-ция F(x)+C также является первообразной f(x).
Совокупность всех первообразных для f(x) назыв. неопределенным интегралом от этой ф-ции и
обозначается. ∫f(x)dx=F(x)+C f(x)-подынтегральная ф-ция, f(x)dx- подынтегральное выражение.
Свойства. 1) (∫f(x)dx)’=(F(x)+C)’=F’(x)=f(x)
2) d∫f(x)dx =(∫f(x)dx)’dx=f(x)dx
3) ∫df(x)dx=∫f’(x)dx =f(x)+C
Теорема. Если f(x) непрерывна на интервале (а,b),то она имеет на нем первообразную.
Геометрический смысл первообразной. ∫f(x)dx =F(x)+C=y эти уравнения определяют множества кривых, которые назыв. интегральными кривыми. Для того чтобы выделить из семейства интегральных кривых одну, задают начальные условия, что равносильно заданию точки, через которую проходит искомая интегральная кривая.
II. Метод замены переменной
∫f(x)dx=|x=φ(t), dx=φ’(t)dt|=∫f(φ(t))φ’(t)dt
30.
32.
Геометрический смысл

1)f(x)≥0 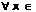 [а,b], то
[а,b], то
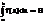
2)f(x) – знакопеременна на [а,b]
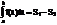
По определению полагаем
1) 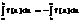 2)
2) 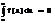
Свойства определенного интеграла:
1) 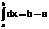
2) 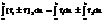
3) 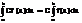
4) Если точка С разбивает[а,b] на [а,с] и [с,b], то интеграл
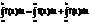
5) 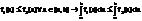
Если
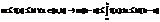

Условный экстремум.
Пусть , где φi — функции, заданные на . Тогда точка называется точкой условного экстремума функции f, заданной на относительно ограничений φi(x) = 0 если она является точкой обычного экстремума на множестве E.
Условный экстремум
Пусть функция
u = f(x1, x2, … , xn)
(1)
определена в некоторой области D М Rn и ее аргументы не являются независимыми переменными, а связаны k (k<n) соотношениями:
Fi(x1, x2, … , xn) = 0 (i = 1,2, … ,k).
(2)
Условия (2) называются уравнениями связи.
Пусть координаты точки M0(x10, … ,xn0) О D удовлетворяют уравнениям связи (2).
Точка M0(x10, … ,xn0) называется точкой условного максимума (минимума) функции (1) при условиях связи (2), если существует такая окрестность Oδ(M0) точки M0 , что для любой точки M(x1, … ,xn) О Oδ(M0) , координаты которой удовлетворяют уравнениям связи (2), выполняется неравенство f(M) ≤ f(M0) (f(M) ≥ f(M0)) .
Методы нахождения условного экстремума
Метод исключения переменных
Ограничимся для простоты случаем n = 2 , k = 1 , т.е. нахождением условного экстремума функции 2–х переменных.
Пусть функция z = f(x,y) определена в некоторой области D М R2 и ее аргументы связаны условием
F(x,y) = 0.
(3)
Допустим, что уравнение (3) определяет неявно функцию y(x) . Тогда можно рассматривать сложную функцию f(x,y(x)) = u(x) . Если эта функция имеет экстремум в точке x0 и y(x0) = y0 , то точка (x0,y0) является точкой условного экстремума функции f(x,y) , аргументы которой удовлетворяют уравнению связи (3).
Если уравнение связи (3) можно разрешить относительно y и перейти от неявного задания функции y(x) к явному, то отыскание условных экстремумов в рассматриваемом случае сводится к отысканию обычных (безусловных) экстремумов функции y(x) .
Метод неопределенных множителей Лагранжа
Пусть функции f(x1, x2, … , xn) и Fi(x1, x2, … , xn) (i = 1,2, … ,k) дифференцируемы в некоторой области D М Rn . Тогда задача отыскания точек условного экстремума функции f(x1, x2, … , xn) при условиях связи
Fi(x1, x2, … , xn) = 0 (i = 1,2, … ,k).
эквивалентна задаче о нахождении точек обычного (безусловного) экстремума функции Лагранжа:
L(x1,x2,:::,xn; λ1,λ2,:::,λk) = f(x1,x2,:::,xn) + λ1 · F1(x1,x2,:::,xn) +
+ λ2 · F2(x1,x2,:::,xn) + … + λk · Fk(x1,x2,:::,xm).
(4)
Схема метода Лагранжа:
1. Составляем функцию Лагранжа (4).
2. Для отыскания стационарных точек функции Лагранжа находим ее частные производные по всем аргументам
∂L
∂x1
= ∂f
∂x1
+ λ1 · ∂F1
∂x1
+ … + λk · ∂Fk
∂x1
,
… … … … …
∂L
∂xn
= ∂f
∂xn
+ λ1 · ∂F1
∂xn
+ … + λk · ∂Fk
∂xn
,
… … … … …
∂L
∂λ1
= F1(x1, x2, … , xn),
… … … … …
∂L
∂λk
= Fk(x1, x2, … , xn)
и приравниваем их к нулю.
Получаем систему (n + k) уравнений с (n + k) неизвестными:
∂f
∂x1
+ λ1 · ∂F1
∂x1
+ … + λk · ∂Fk
∂x1
= 0,
… … … … …
∂f
∂xn
+ λ1 · ∂F1
∂xn
+ … + λk · ∂Fk
∂xn
= 0,
… … … … …
F1(x1, x2, … , xn) = 0,
… … … … …
Fk(x1, x2, … , xn) = 0.
Если (x10,:::,xn0; λ10,:::,λk0) — решение этой системы, то оно определяет стационарную точку (x10,:::,xn0) функции f(x1,x2,:::,xn) при условиях связи (2), в которой функция может иметь условный экстремум.
3. Чтобы установить наличие или отсутствие условного экстремума в каждой стационарной точке M0 , нужно исследовать знак 2–го дифференциала функции Лагранжа
d2L(M0) = n ∂2L
∂xi∂xj
(M0) dxidxj
∑
i, j = 1
при значениях дифференциалов dx1, … ,dxn , не равных одновременно нулю и удовлетворяющих продифференцированным уравнениям связи
∂fi(M0)
∂x1
dx1 + … + ∂fi(M0)
∂xn
dxn = 0, i = 1,
… ,k.
Замечание. При решении практических задач во многих случаях наличие условного экстремума в стационарной точке определяется существом задачи.
Обоснование метода Лагранжа для случая n = 2 , k = 1 приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики: Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М.: Изд–во МЭИ, 2002 (стр. 170).
Геометрический смысл условного экстремума функции:
Условными экстремумами функции z = f(x,y) при F(x,y) = 0 являются ее экстремумы на линии, образующейся в сечении поверхности z = f(x,y) цилиндрической поверхностью F(x,y) = 0 .
¾¾¾¾ * * * ¾¾¾¾
Предел и непрерывность.
Определение. Окрестностью радиуса r точки М0(х0,y0)называется множество точек М(x,y) координаты которых удовлетворяют неравенству
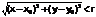
Определение. Число А называется пределом функции f(x,у) при М(х;у)->М0(х0,у0), если для любого наперед заданного ε > 0 существует такой радиус r, что для всех точек из окрестности радиуса r точки М0 выполняется:
| f (x,y) - f (x0,y0)| < E и обозначается
A=lim {x→х0 y→у0} f (x;y)
причем x;y стремятся к точке М0 произвольным образом.
Замечание. В некоторых случаях предел функции зависит от порядка вычисления предела по аргументам.
Определение. Функция f (х;у) называется непрерывной в точке M0, если в окрестности этой точки выполняется соотношение
(3) Lim{ x→х0;y→у0} f(x,y) = f(x0;y0)
Определение. Функция, непрерывная во всех точках области, называется непрерывной в этой области,
преобразуем соотношение
Lim {∆x →0 ∆y→0 }[f(x,y) - f(x0;y0)]=0
Так как x→x0 и y→y0, x=x0 + ∆x, y=y0 + ∆y, ∆x→0, ∆y→0
То имеем
Lim{∆x→0, ∆y→0} [f(x0 + ∆x, y0 + ∆y) - f(x0;y0)]=0
Определение. Если предел полного приращения при ∆х →0 и ∆y→0 равняется нулю, то функция называется непрерывной в точке x0,y0.
Определение. Точка разрыва x1,y1, может быть в следующих случаи:
1.Функция f(x,у) в точке х1, у1 не определена.
2.Функция f(x, у) определена в самой точке и в окрестности ее, a предел не существует
З.Существует предел функции, функция определена в точке в и ее окрестности, но не выполняется равенство (3) при х→х1, у→y1
Трехкратный
Так же, как и для правильной области D опишем условия, которым должно удовлетворять правильное трехмерное тело V. 1) любая прямая, параллельная оси Oz, проведенную через внутреннюю точку тела V, пересекает поверхность S не более чем в двух точках, 2) все тело V проецируется на плоскость xOy в правильную двухмерную область D. Всякая часть тела V,отсеченная плоскостью, параллельной любой из координатных плоскостей xOy, xOz, yOz, также обладает этими же свойствами. Пусть дано правильное тело, ограниченное сверху гладкой поверхностью z=χ2(x,y), а снизу поверхностью z= χ1(x,y), причем это тело проецируется на плоскость xOy в виде правильной области D, которая задается уравнениями a≤x≤b; φ(x) ≤y≤ψ(x).
Предположим, что нижняя и верхняя поверхности тела гладкие, т.е функции непрерывны по обеим переменным x,y. Рассмотрим выражение 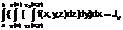 (1) . Выражение (1) называется трехкратным интеграломи обозначается JV.
(1) . Выражение (1) называется трехкратным интеграломи обозначается JV.
Двойные интегралы, их свойства
Пусть функция z=f(x;y) определена в ограниченной замкнутой области D плоскости xOy. Разобьем D произвольным образом на n элементарных областей, имеющих площади 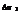 ,
, 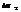 ,…,
,…, 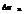 и диаметры d1,d2,…,dn (наибольшее расстояние между двумя точками границы области называется диаметром области). Выберем в каждой элементарной области произвольную точку Pk(ξk,ηk) и умножим значение функции в точке Pk на площадь данной области.
и диаметры d1,d2,…,dn (наибольшее расстояние между двумя точками границы области называется диаметром области). Выберем в каждой элементарной области произвольную точку Pk(ξk,ηk) и умножим значение функции в точке Pk на площадь данной области.
Выражение 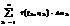 называется интегральной суммойдля функции f(x,y) по области D. Если при max dk →0 интегральная сумма имеет конечный предел
называется интегральной суммойдля функции f(x,y) по области D. Если при max dk →0 интегральная сумма имеет конечный предел 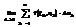 , то этот предел называется двойным интегралом от функции f(x,y) в области D и обозначается
, то этот предел называется двойным интегралом от функции f(x,y) в области D и обозначается 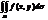 =
= 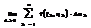 или
или 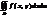 =
= 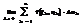 . Геометрический смысл двойного интеграла: если f(x,y)>0 в области D, то двойной интеграл численно равен объему цилиндрического тела с основанием D, ограниченному сверху поверхностью z=f(x,y). Если функция f(x,y) непрерывна в замкнутой области D, то двойной интеграл существует. Основные свойства двойного интеграла:
. Геометрический смысл двойного интеграла: если f(x,y)>0 в области D, то двойной интеграл численно равен объему цилиндрического тела с основанием D, ограниченному сверху поверхностью z=f(x,y). Если функция f(x,y) непрерывна в замкнутой области D, то двойной интеграл существует. Основные свойства двойного интеграла:
1) 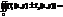
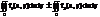
2) 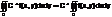
3) 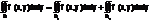
D=D1+D2.
4) m≤f(x,y)≤M → mS≤ 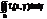 ≤MS.
≤MS.
Билет. Основные понятия (определение, порядок, общее и частное решение и интеграл, задача Коши, теорема существования и единственности).
Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы). Если независимая переменная одна, то уравнение называется обыкновенным, если же переменных две или больше, то уравнение называется дифференц. уравнением в частных производных. Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Решением дифференц. уравнения называется такая функция y=φ(x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференц. уравнения называется интегрированием уравнения. Общим решением уравнения y’=f(x,y) называется функция y= φ(x,С). Всякое решение y= φ(x,С0), получающееся из общего при конкретном значении C=C0 ,называется частным решением. Если зависимость x от y находится в неразрешенном относительно y виде, то его называют общим интегралом.
F(x,y,y’)=0 – общий вид дифференциального уравнения первого порядка или в разрешенном относительно y’ виде: y’=f(x,y) (1). Пусть требуется найти функцию y(x), являющуюся решением уравнения (1) и удовлетворяющую условию: y(x0)=y0 (2). Такая задача называется задачей Коши или начальной задачей, а условие (2) называется начальным условием.Теорема существования и единственности решения( Теорема Пикара, Пеано, Коши): Если функция f(x;y) непрерывна в ограниченной области D, содержащей M0(x0;y0) – начальную точку, т.е. |f(x;y)|≤M, M>0 и если частная производная по y в той же области D ограниченна, т.е. | 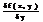 |≤K, K>0, то существует единственное решение дифференц. уравнения (1), удовлетворяющее условию (2). Это решение будет непрерывно дифференцируемым в окрестности начальной точки. Геометрически это означает, что проходит единственная кривая через точку M0(x0;y0), уравнение которой удовлетворяет дифференциальному уравнению.
|≤K, K>0, то существует единственное решение дифференц. уравнения (1), удовлетворяющее условию (2). Это решение будет непрерывно дифференцируемым в окрестности начальной точки. Геометрически это означает, что проходит единственная кривая через точку M0(x0;y0), уравнение которой удовлетворяет дифференциальному уравнению.
Уравнения, не содержащие y.
f(x,y(k),y(k+1),…,y(n))=0. Рассмотрим уравнения с n=2.
f(x,y’,y’’)=0. Замена: y’=p(x); y’’=p’;
Уравнения, не содержащие x.
f(y,y’,…,y(n))=0. Рассмотрим уравнения с n=2.
f(y,y’,y’’)=0 Замена: y’=p; y’’=p∙(dp/dy)
Признаки сравнения.
Рассмотрим 2 ряда:
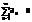
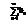 , причём 0≤an≤bn
, причём 0≤an≤bn
1 признак: Тогда, зная, что ряд b сходится, можно утверждать, что ряд а тоже сходится; если ряд а расходится то и ряд b тоже расходится. И никак не наоборот!
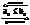
2 признак:Если существует  то ряды a и b сходятся или расходятся одновременно.
то ряды a и b сходятся или расходятся одновременно.
Признак Лейбница
Признак Лейбница — признак сходимости знакочередующегося ряда,Формулировка теоремы:
Пусть для ряда 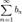 выполняются следующие условия: 1. знакочередование (например: выполняются следующие условия: 1. знакочередование (например: 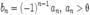 ) 2. an + 1 < an (монотонное убывание {an}) 3. ) 2. an + 1 < an (монотонное убывание {an}) 3. 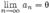 . Тогда этот ряд сходится. . Тогда этот ряд сходится. |
Замечание: Если, выполнены все условия, и ряд из модулей сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно.Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
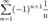 . Ряд из модулей иммет вид
. Ряд из модулей иммет вид 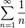 - это гармонический ряд, который расходится.
- это гармонический ряд, который расходится.
Теперь воспользуемся признаком Лейбница:
1. знакочередование выполнено 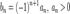
2. 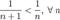
3. 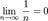 .
.
Следовательно, т.к. все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
Тройной интеграл
Тройным интегралом называют кратный интеграл с 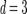 .
.
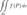 Здесь
Здесь 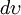 — элемент объема в рассматриваемых координатах.
— элемент объема в рассматриваемых координатах.
В прямоугольных координатах 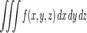 , где
, где 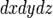 является элементом объема в прямоугольных координатах.
является элементом объема в прямоугольных координатах.
Числовые последовательности. Предел последовательности. Предел функции.
Определение: Числовой последовательностью назыв множество чисел, пронумерованных с помощью натуральных чисел и расположенных в порядке возрастания их номеров.
у1, у2, …, уn={yn}→yn=f(n), где у1, у2 –члены, yn=f(n) –общий член последов.
Определение: Число а назыв пределом последов, если 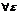 >0, сколь угодно малого
>0, сколь угодно малого 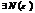 , что для всех n> N(
, что для всех n> N( 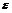 ), выполняется
), выполняется 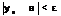 , при этом
, при этом
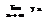 =a, (a-ε;a+ε) - окрестность
=a, (a-ε;a+ε) - окрестность
Геометрическая интерпретация
y=f(x) – ф-ция, х - аргумент ф-ции, х→а, f(x) →А, А предел ф-ции
Определение: числа А назыв. пределом ф-ции f(x) при х→а, если 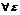 >0, сколь угодно малого,
>0, сколь угодно малого, 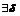 >0, что для всех x, для которых выполняется условие
>0, что для всех x, для которых выполняется условие 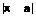 <
< 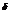 , имеет место
, имеет место 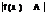 <
< 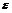
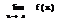 =A
=A
Замечание: 1) х→а как угодно; 2) f(x) в точке а может быть и не определена.
Определение: числа А назыв. пределом ф-ции f(x) при х→∞, если 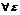 >0, сколь угодно малого,
>0, сколь угодно малого, 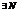 , что для всех x,|x|>N , выполняется.
, что для всех x,|x|>N , выполняется. 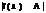 <
< 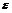
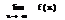 =A
=A
Теорема: Любая функция, имеющая предел, является ограниченной.
