Производные высших порядков от функций, заданных параметрически

Пусть функция у=ƒ(х) задана параметрическими уравнениями

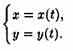
Как известно, первая производная у'х находится по формуле (23.1)

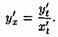
Найдем вторую производную от функции заданной параметрически. Из определения второй производной и равенства (23.1) следует, что

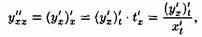
Дифференциал функции и его геометрический смысл

Понятие дифференциала функции

Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.

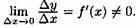
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/D х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.

Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как 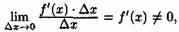а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:

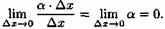
Поэтому первое слагаемое ƒ'(х)· ∆х называют главной частью приращения функции ∆у.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х. (24.1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так:

dy=ƒ'(х)dх, (24.2)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение

производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.

Геометрический смысл дифференциала функции

Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х, |AM₁|=∆у. Из прямоугольного треугольника МАВ имеем:

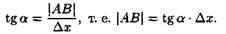
Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

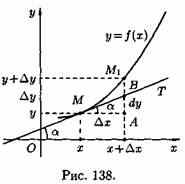
В этом и состоит геометрический смысл дифференциала.

Дифференцируемость функции

Функция y=f(x)называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения 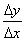существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.