Исследование функций и построение графиков.

Под «исследованием функции» понимают изучение её поведения (изменения) в зависимости от изменения аргумента. На основании исследования функции строят её график, предварительно изображая характерные точки.

Исследование функций и построение графиков можно проводить по следующей схеме.

1. Найти область определения функции.

2. Исследовать вопрос о чётности функции, о периодичности.

3. Найти точки пересечения графика функции с осями координат.

4. Изучить поведение функции при стремлении аргумента к концам промежутков области определения.

5. Найти точки экстремумов, промежутки возрастания и убывания функции.

6. Определить промежутки выпуклости функции, найти точки перегиба.

7. Найти асимптоты графика функции.

Порядок исследования иногда целесообразно выбирать исходя из конкретных особенностей данной функции.

.

Понятие о первообразной функции.

Определение.Функция F(x), определённая в промежутке (а;b), называется первообразной данной функцииf(x) в этом промежутке, если для любого значения хÎ(а;b) выполняется равенство F'(x) = f(x).

Теорема 1.Если F(x) ─ первообразная функции f(x), то множество

{F(x) + CôC ─ произвольная постоянная}

есть множество всех первообразных функции f(x).

Доказательство.Очевидно, что любая функция Ф(х) = F(x) + C₀, где С₀ ─ некоторая постоянная, является первообразной функции f(x), т.к. Ф'(х)= (F(x) + C₀)' = F'(x) + C'₀= f(x). Обратно, если Ф(х) ─ некоторая первообразная функции f(x), то

(Ф(х) – F(x))' = Ф'(х) – F'(x) = f(x) – f(x) = 0. Но это означает, что функция Ф(х) – F(x) постоянна, т.е. существует произвольная постоянна С₁ такая, что Ф(х) – F(x) = С_1, откуда Ф(х) = F(x) + С₁.

Неопределённый интеграл и его свойства.

Определение.Если функция F(x) ─ первообразная функции f(x), то множество всех функций F(x) + С, где С ─ произвольная постоянная, называется неопределённым интеграломот функции f(x) и обозначается

ò f(x)dx = F(x) + C.

При этом функция f(x) называется подинтегральной функцией,f(x)dx ─ подинтегральным выражением.Операция нахождения неопределённого интеграла называется также интегрированием.

Свойство 1.Производная неопределённого интеграла равна подинтегральной функции; дифференциал от неопределённого интеграла равен подинтегральному выражению, т.е.

(ò f(x)dx)' = f(x); d(ò f(x)dx) = f(x)dx.

Свойство 2.Неопределённый интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

ò d(j(x)) = j(x) + С.

Свойство 3.Постоянный множитель можно выносить за знак неопределённого интеграла, т.е.

ò k×f(x)dx = k×ò f(x)dx (k = const, k¹0).

Свойство 4.Если функции f₁(x) и f₂(x) имеют первообразные, то функция f₁(x) + f₂(x) также имеет первообразную, причём

ò (f₁(x) + f₂(x))dx = ò f₁(x)dx + ò f₂(x)dx.

Свойство 4.1.Если функции f₁(x), f₂(x),…, f_n(x) имеют первообразные, то функция

f₁(x) + f₂(x) +…+ f_n(x) также имеет первообразную, причём

ò (f₁(x) +…+ f_n(x))dx = ò f₁(x)dx + … +ò f_n(x)dx..

Таблица основных неопределённых интегралов.

1. òdx = x + C, 6. òcosxdx = sinx + C,

2. òx^adx = 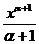+ C,(a > 0) 7. òsinxdx = - cosx + C,

3. ò dx = ℓnôxô+ C, 8. ò 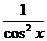dx = tgx + C,

4. òa^xdx = 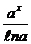+ C, (a > 0) 9. ò 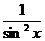dx = - ctgx + C,

5. òe^xdx = e^x + C, 10. ò 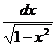=arcsinx + C =-arccosx+ C

11. ò 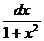dx = arctgx + C = - arcctgx + C.

Замечание.Формулы этой таблицы остаются справедливыми и в случае, когда вместо х поставить некоторую дифференцируемую функцию u = u(x), т.е. можно записать обобщённую таблицупростейших неопределённых интегралов:

1. òdu = u + C, 2. òu^adu = 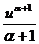+ C (a ¹ 1)

и т.д.