Достаточное условие разложение ф-й в степенные ряды
Если в некотором интервале, содержащем точку 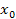 , абсолютные величины всех пр-х ф-ии f(x)ограничены одним и тем же числом M
, абсолютные величины всех пр-х ф-ии f(x)ограничены одним и тем же числом M 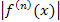 ≤M, n=1,2…, то ф-я f(x) в этом интервале разлагается в ряд тейлора.
≤M, n=1,2…, то ф-я f(x) в этом интервале разлагается в ряд тейлора.
18. Вычисление площадей плоских фигур:
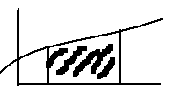 1.
1. 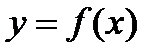 на
на 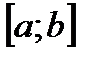 и
и 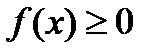
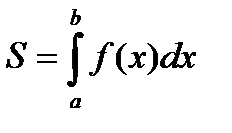
 2.
2. 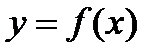 на
на 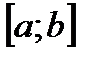 и
и 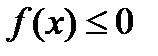
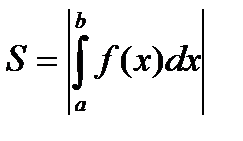
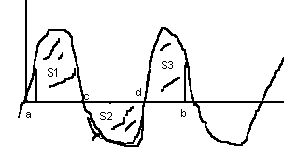 3.
3. 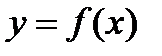 на
на 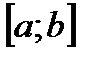 график имеет вид
график имеет вид
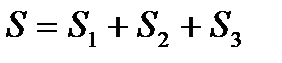
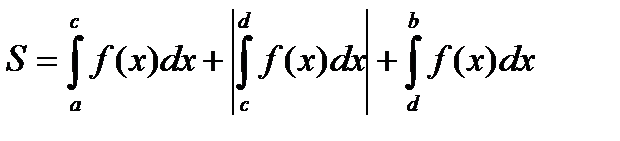
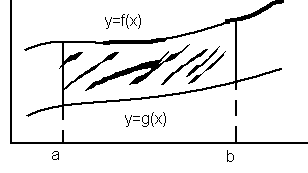 4. даны две функции:
4. даны две функции: 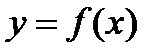 и
и 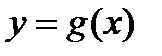 на промежутке
на промежутке 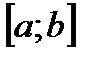

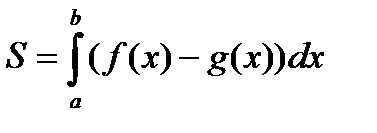
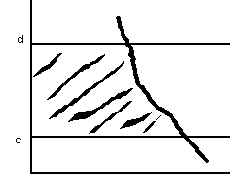 5.
5. 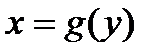 на промежутке
на промежутке 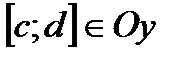 то получаем
то получаем 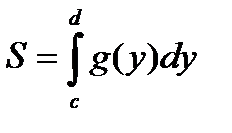
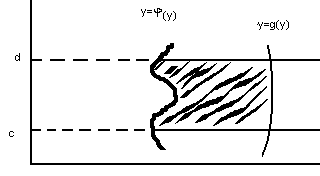 6.
6. 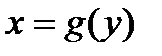 и
и 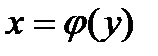 на промежутке
на промежутке 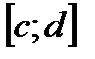 (графики ориентированны на
(графики ориентированны на 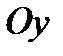 )
) 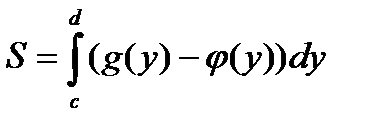
Длина дуги плоской кривой.
Пусть некот. линия y=f(x), где f(x) – дифф. на отрезке [a; b]
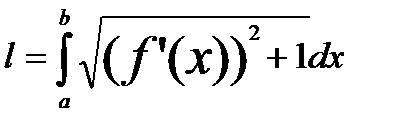 - длина дуги АВ
- длина дуги АВ
Y(k-1) M(k-1)
M1
Yk A Mk
M(n-1) B
a=x0 x1 x2 xk x(n-1) b=xn
Вычисление объёмов тел вращения.
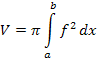
Неберущиеся интегралы.
Опрерация дифференц-я не выводит нас из класса элемент.ф-й. С операцией интегрир. дело обстоит иначе: интегралы от некот. элемент. ф-й уже не явл. элемент. ф-ми. Например: 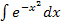 – интег. Пуассона;
– интег. Пуассона; 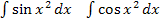 – инт. Френеля;
– инт. Френеля;
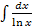 – интег.логарифм,
– интег.логарифм,
Евклидова плоскость и евклидово пр-во
Координатную плоскость называют евклидовой плоскостью, если расстояние между двумя любыми точками 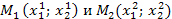 определяется по ф-ле
определяется по ф-ле
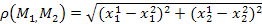
Аналогично вводится понятие трёхмерного евклидово пр-ва. В этом случае каждая точка М коорд. пр-ва хар-ся упорядоченной тройкой чисел 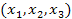 , а расстояние между любыми двумя точками пр-ва
, а расстояние между любыми двумя точками пр-ва 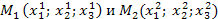 опред-ся ф-лой
опред-ся ф-лой
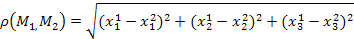
Понятие функции нескольких переменных.
Пусть имеется 2 непустых множества: DÌR(в квадрате),UÎR. Если каждой паре чисел "(x,y)ÎDy; по некоторому правилу поставлен в соответствии 1 единственный элемент из множества U, то говорят, что на множестве D задана функция со значениями во множестве U, при этом пишут, что f: D®U. Множество D называется областью определения функции, множество U, состоящее из чисел f(x,y), где пара (x,y)ÎD ,называется областью значений функции. Функциональная зависимость: U=f(x,y). Аналогично определяется функция нескольких переменных. Областью определения 2-х переменных может быть плоскость, часть плоскости, ограниченная некоторой замкнутой прямой, либо совокупность нескольких частей плоскости. Ф-ю неск. веществ. перем. Как и ф-ю одной перем., можно задать аналитическим, табличным или описат. способом.
Графиком ф-и z=(f,y) ((x,y) 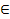 Ω) назыв. мн-во точек в пр-ве R³,коорд. x,y, кот. принад.Ω, а z нах. по ф-ле z=(f,y).Даже для ф-и 2х перем. изуч. и изобр. график ф-и затруднит. С целью изуч. граф. ф-и будет понятие линии ур-ня. Линией ур-ня С наз. совок. точек на плоск. Оху, для кот. (f,y)=С(const). В эк. линией ур-ня наз. изоквантами, изокостами в завис. от того, какой эк. проц. изучается.
Ω) назыв. мн-во точек в пр-ве R³,коорд. x,y, кот. принад.Ω, а z нах. по ф-ле z=(f,y).Даже для ф-и 2х перем. изуч. и изобр. график ф-и затруднит. С целью изуч. граф. ф-и будет понятие линии ур-ня. Линией ур-ня С наз. совок. точек на плоск. Оху, для кот. (f,y)=С(const). В эк. линией ур-ня наз. изоквантами, изокостами в завис. от того, какой эк. проц. изучается.
Предел функции нескольких переменных в точке и его свойства.
Число А называется пределом функции f(x,y), при x®xo, y®yo, если для любой последовательности точек "(xn,yn), сходящейся к точке (xо,yо), но не равной (xо,yо), соответствующая последовательность значений функции f(xn,yn) сходится к числу А. f(xn,yn)®A
Св-ва:
1. арифметические операции
2. Если ф-я f имеет предел в т. Ро, то она ограничена в некот. Ебселент-окрестности т. Ро
3. Если 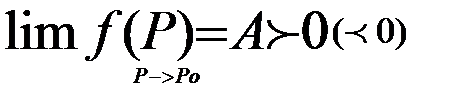 , то сущ. такая Ебселент-окрестность т.Ро, к кот. f(P)>0 (<0).
, то сущ. такая Ебселент-окрестность т.Ро, к кот. f(P)>0 (<0).
