Критерий Келли в блек-джеке, спортивных тотализаторах и на фондовой бирже.
Критерий Келли в блек-джеке, спортивных тотализаторах и на фондовой бирже.
Эдвард О. Торп
Примечание перев.: замечания по переводу принимаются по адресу [email protected] (Киселев Дмитрий).
В данной редакции отсутствуют приложения – см. оригинал на англ.:
Abstract, Chapters 1 - 10 (2.5M)
Figures, Appendices, and References (750K)
Аннотация
Центральная проблема для игроков – найти и заключить пари с положительным ожидаемым выигрышем. Но игрокам также необходимо знать, как управлять их деньгами, т.е. сколько ставить. На фондовых рынках (включая рынок ценных бумаг) проблема подобна этой, но более сложна. Игрок, который теперь является инвестором, ищет «большую прибыль при управляемом уровне риска». В обоих этих случаях, мы исследуем использование критерия Келли, который максимизирует ожидаемую величину логарифма дохода («максимизирует ожидаемую логарифмическую полезность»).
Этот критерий известен экономистам и теоретикам-финансистам под такими именами как «стратегия максимизации геометрического среднего портфеля», максимизация логарифмической полезности, стратегия оптимального роста, критерий роста капитала и т.д.
Автор начал практическое применение критерия Келли с использования его для счета карт в блэк-джеке. Мы представим некоторые полезные формулы и методы, чтобы ответить на различные естественные вопросы об этом, которые возникают в блэк-джеке и других азартных играх. Затем мы проиллюстрируем его недавнее использование в успешных системах ставок для спортивных тотализаторов. В заключении, мы обсудим его приложение к рынку ценных бумаг, где эти методы помогли автору сделать за тридцать лет в общей сложности «ставок» на сумму 80 миллиардов долларов.
Пересмотрено 29 мая 1998 года
Введение
Фундаментальной проблемой в играх является поиск возможностей ставок с положительным ожиданием. Аналогичная проблема в инвестировании – поиск возможностей инвестирования с «избыточной», с учетом поправок на риск, доходностью. Как только такие благоприятные возможности идентифицированы, игрок или инвестор должен решить, какую часть своего капитала поставить на кон (вложить). Именно эту проблему мы здесь рассматриваем. Интерес к ней существует по крайней мере с восемнадцатого столетия, с обсуждения Даниилом Бернулли Санкт-Петербургского Парадокса (Feller, 1966).
Один подход состоит в том, чтобы минимизировать вероятность «потерять все» в пределах определенного числа попыток N. Примером другого подхода будет - максимизировать вероятность достижения установленной цели за N попыток (Browne, 1996).
Другой подход, наиболее изученный экономистами и не только, состоит в том, чтобы оценить деньги, используя функцию полезности. Она обычно определена для всех неотрицательных вещественных чисел, имеет вещественные значения и является не убывающей (большее количество денег по крайней мере столь же хорошо как меньшее количество денег). Некоторые примеры - U(x) = xα, 0 ≤ α < ∞ и U(x) = log x, где log означает loge, а log 0 = -∞. Как только функция полезности определена, цель состоит в том, чтобы максимизировать ожидаемую величину полезности капитала.
Даниил Бернулли использовал функцию полезности log x, чтобы "решить" Cанкт-Петербургский Парадокс. (Но решение не устраняет парадокс, потому что каждая функция полезности, которая не ограничена сверху, включая log, представляет собой измененную версию Санкт-Петербургского Парадокса.) Функция полезности log x была вновь использована J.L. Kelly (1956), показавшим, что она имеет некоторые замечательные свойства. Они были изучены и обобщены в исследовании Brieman (1961). Markowitz (1961) применяет ее к ценным бумагам. Дускуссии о критерии Kelly ("критерий среднего геометрического") с точки зрения финансов, см. McEnally (1986), там же приводятся дополнительные исторические справки и ссылки.
Меня со статьей Kelly познакомил Claude Shannon в Массачучетском Технологическом (M.I.T) в 1960, вскоре после того, как я создал математическую теорию счета карт для блэк джека. Критерий Келли заключался в нахождении величины ставки для каждой попытки, такой что она максимизировала E [log X], ожидаемую величину логарифма капитала X (случайная переменная). Я использовал его в реальной игре и представил это сообществу игроков в первом издании "Beat the Dealer", Thorp, (1962). Если все ставки блэк джека имеют положительное ожидание и независимы, ставки Келли, при игре на одну сдачу будут чрезвычайно просты: ставьте долю вашего текущего капитала, равную вашему ожиданию. На практике эта оценка несколько меняется (как правило снижается) для того, чтобы допустить возможность "ждущих ставок", имеющих некоторое отрицательное ожидание, при более высоких колебаниях, возникающих из-за выплат, больших, чем один к одному, и когда играются больше одной сдачи одновременно.
Вот свойства, которые сделали критерий Келли столь привлекательным. Для простоты понимания мы проиллюстрируем его на примере самого простейшего случая - подбрасывания монеты, но концепция и выводы легко обобщаются.
Подбрасывание монеты
Допустим, мы играем с бесконечно богатым противником, который будет делать повторяющиеся ставки на независимые события – броски монеты. Далее, предположим, что при каждом броске наша вероятность победы p> 1/2, а вероятность потери q = 1 - p. Наш начальный капитал - XO. Предположим, что наша цель – максимизация ожидаемой величины E (Xn) через n попыток. Сколько мы поставим, Bk, на k-ой попытке? Пусть Tk = 1, если k-я попытка - выигрышная и Tk = -1, если она проиграна, тогда Xk =Xk-1 + Tk Bk для k = 1,2,3.., и Xn = XO + Σnk=1TkBk. Тогда
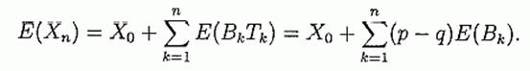
Так как игра имеет положительное ожидание, то есть p-q> 0, в этой ситуации равных выплат, для того, чтобы максимизировать Е(Хn), мы должны были бы максимизировать E(Bk) для каждой попытки. Таким образом, чтобы максимизировать ожидаемый рост мы должны ставить все наши ресурсы в каждой попытке. Таким образом, B1 = X0 , и, если мы выигрываем первую ставку, B2 = 2X0, и т.д. Однако, вероятность краха при этом будет 1 - pN и при p < 1, lim n→∞ [1 —рn] = 1 , так что крах почти неизбежен. Таким образом, "смелый" критерий ставок для максимизации ожидаемого роста обычно нежелателен.
Аналогично, если наша стратегия состоит в том, чтобы минимизировать вероятность возможного краха (а "крах" происходит, если XK = 0 на k-ой попытке) широко известная формула краха игрока (по Feller (1966)) показывает, что мы минимизируем крах, делая минимальную ставку на каждой попытке, но это, к сожалению, также минимизирует и ожидаемый рост. Таким образом, "робкая" система ставок также непривлекательна.
Это предполагает существование промежуточной стратегия, которая лежит где-то между максимизацией E (Xn) (и верным крахом) и уменьшением вероятности краха (и уменьшением E (Хn)). Асимптотически оптимальная стратегия была впервые предложена J.L. Kelly (1956).
Так как вероятности и выплаты при каждой ставке в описанной игре с подбрасыванием монеты одинаковы, кажется вполне правдоподобно, что "оптимальная" стратегия потребует всегда держать пари на одну и ту же долю f вашего капитала. Чтобы это было возможным сделать, мы предполагаем далее, что капитал может бесконечно дробиться. Это предположение обычно не имеет большого значения в практическом применении.
Стратегия, в которой ставки делаются согласно Bi = f Xi-1, где 0 ≤ f ≤ 1, иногда называется стратегией "фиксированной доли". Пусть S и F - числа успехов и проигрышей в n попытках соответственно, тогда наш капитал после n попыток равен Xn = Xo(1+ f)S (1-f)F, где S + F = n. При f в интервале 0 < f < 1, Рr (Хn = 0) = 0. Таким образом, "краха", понимаемом в техническом смысле как разорение игрока, произойти не может. "Крах" впредь будет означать, что для произвольно маленького положительного ε, limn→∞[Рr(Xn ≤ ε)] = 1. В этом смысле, как мы увидим, крах все-таки может случиться при некоторых обстоятельствах.
Отметим, что так как
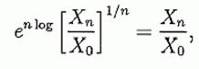
величина
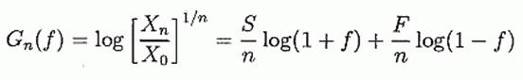
измеряет экспоненциальную скорость роста за попытку. Kelly максимизировал ожидаемую величину коэффициента скорости роста, g(f), где 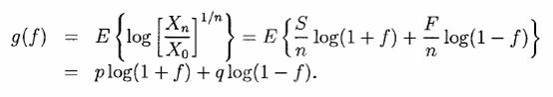
Обратите внимание, что g(f) = (1/n)E[logXn]- (1/n)logX0, поэтому, для фиксированного n, максимизация g(f) - то же самое, что максимизация E[logXn]. В дальнейшем обсуждении мы в основном будем говорить о максимизации g(f). Заметим, что
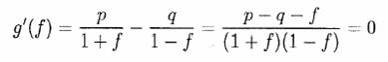
когда f = f * = p - q.
Так как
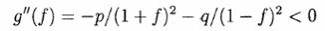
то g' (f) убывает строго монотонно на [0, 1), Так как g' (0) = p-q > 0 и lim f→1 - g'(f) = - ∞. Вследствие непрерывности g'(f), g (f) имеет единственный максимум в точке f=f *, где g(f *) = p log p + q log q + log 2 > 0. Более того, поскольку g(0) = 0 и lim f→1 - g{f) = - ∞, то существует единственное fC > 0, такое что 0 < f* < fC < 1 и g(fC) = 0. Природа функции g(f) теперь очевидна, и график g(f) от f выглядит так, как показано на Рисунке 1.
Следующая теорема излагает важные преимущества максимизации g(f). Детали здесь опущены, но доказательства (i), (ii), (iii), и (vi) для простого биномиального случая могут быть найдены в Thorp (1969); более общее доказательство этого, а также доказательства (iv) и (v) можно найти у Breiman (1961).
Теорема 1 (i) Если g(f) > 0, тогда почти достоверно, что limn→∞ Хn = ∞, то есть для каждого М, Pr [lim n→∞ inf Хn > М] = 1;
(ii) если g(f) < 0, тогда почти достоверно, что limn→∞ Хn = 0, то есть для каждого ε>0,Pr [lim n→∞ sup Хn < ε] = 1;
(iii) Если g(f) = 0, тогда почти достоверно, что lim n→∞ sup Хn= ∞ и lim n→∞ inf Хn = 0.
(iv) Для заданной стратегии Ф*, которая максимизирует E[log Xn] и любой другой "существенно иной" стратегии Ф (не обязательно стратегии фиксированных дробных ставок) почти достоверно, что limn→∞ Хn(Ф*)/Хn (Ф) = ∞.
(v) Ожидаемое время, необходимое чтобы текущий капитал Xn достиг заранее установленного значения С будет, асимптотически, наименьшим при стратегии, которая максимизирует E[log Xn].
(vi) Предположим, что отдача от одной ставки на i-ой попытке - биноминальная случайная переменная Ui, далее предположим, что вероятность успеха pi, где 1/2 < pi < 1. Тогда E[log Xn] максимизируется выбором значением для ставки при каждой попытке доли f *i = pi - qi которая максимизирует E[ log (1+fiUi)].
Часть (i) показывает что, если бы не конечное время, благосостояние игрока XN превысило бы любой установленный предел М, когда f выбрано в интервале (0, fс). Но, если f > fC , часть (ii) показывает, что крах почти неизбежен. Часть (iii) демонстрирует, что, если f = fC, Хn будет (почти достоверно) беспорядочно колебаться между 0 и + ∞, Таким образом, утверждение одного из авторов, что Xn → X0 при n → ∞, когда f = fс, явно противоречиво. Части (iv) и (v), показывают, что стратегия Kelly максимизирования E[logXn] является асимптотически оптимальной в соответствии с двумя важными критериями. "Существенно иная " стратегия - одна из таких, что разница E[ ln Xn*] – E[ lnXn] между стратегией Kelly и другой стратегией растет быстрее, чем стандартное отклонение ln Xn* - ln Xn, обеспечивая Р (ln Xn* - ln Xn > 0) → 1. Часть (vi) устанавливает справедливость использования метода Kelly выбора fi* при каждой попытке (даже если от одной попытки к следующей меняется вероятность) для максимизации E[log Xn].
Пример 2.1 Игрок А играет против бесконечно богатого противника. Игрок выигрывает одну и ту же сумму при последовательных независимых бросках монеты с вероятностью p =0,53 (независимые события). Игрок А имеет начальный капитал X0 , и капитал может бесконечно делиться. Применяя Теорему 1 (vi), f* = p - q = 0,53 – 0,47 = 0,06, Таким образом, в каждой игре он должен ставить 6 % текущего капитала,чтобы Xn рос с максимальной скоростью и с нулевой вероятностью краха. Если Игрок А постоянно ставит меньшую долю, чем 6 %, Xn также будет расти до бесконечности, но медленнее.
Если Игрок A постоянно ставит долей большей чем 6 %, но меньше fс , возникает то же самое. Решая уравнение g(f) = 0,53log (l +f) + 0,47log (l - f)=0 численно на компьютере получаем fc = 0,11973¯. Так, если ставка больше чем примерно 12 %, то даже при том, что Игрок А может временно наслаждаться быстрой скоростью роста, возможные колебания вниз непременно приведут величину Xn к нулю. Вычисление дает коэффициент роста g(f*)= f (0,06) = 0,001801 так, что после n последовательных ставок логарифм среднего величины капитала Игрока А будет стремиться к значению в 0,001801*n раз превышающему стартовый капитал. Приравнивая 0,001801n = log 2, получаем ожидаемое время, необходимое для удвоения капитала примерно равное n = 385.
Критерий Кэлли может легко быть расширен на игры с неравными выплатами. Предположим, Игрок А выигрывает b единиц на каждую единицу ставки. Далее предположим, что на каждой попытке вероятность победы p> 0 и pb - q> 0, так что игра выгодна для Игрока А. Методы, подобные рассмотренным, могут использоваться для максимизации
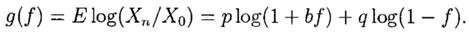
Вычисления дают f* = (bp - q)/b, оптимальную долю текущего капитала, которая должна быть поставлена в каждой игре, чтобы максимизировать коэффициент роста g(f).
Эта формула для f * появилась в Thorp (1984) и была предметом обсуждения в апреле 1997 в интернете на сайте Станфорда Вонга http://bj21.com . Один из обсуждавшихся там вопросов состоял в том, что можно потерять только равные по величине ставки, так что нет оснований рассматривать простое обобщение этой формулы для ситуации, когда единица ставки выигрывает b с вероятностью p> 0 и теряет a с вероятностью q. Тогда, если ожидание m ≡ bp - aq > 0, f* > 0 и f* = m/ab. Обобщение, однако, необходимо. Можно покупать в кредит на финансовых рынках и терять гораздо больше ставки. Примеры: покупка товарного фьючерса или короткая продажу (когда потеря потенциально неограничена). См., например, Thorp и Kassouf (1967).
Педанты, которые настаивают, что эти выплаты не биноминальны, могут рассмотреть короткую продажу способом двоичных чисел. Эти способы описаны у Browne (1996).
Критика, иногда звучащая в адрес стратегии Kelly – то, что капитал на самом деле не делится бесконечно. В реальном мире, ставки - умноженные минимальные единицы, типа 1 $ или 0,01 $. На рынках ценных бумаг, где система учета компьютеризованна, минимальная единица может быть сколь угодно малой. С учетом минимально позволенной ставки "крах" в обычном смысле возможен всегда. Не трудно показать, однако, (см. Thorp и Waiden, 1966) что, если минимальная позволенная ставка невелика относительно начального капитала игрока, то, вероятность краха в обычном смысле незначительна, а также то, что теория, описанная здесь, является полезной аппроксимацией. Этот раздел написан согласно работе Rotando and Thorp (1992).
Блэк джек
Обсуждение игры в блэкджек в целом смотрите Thorp (1962, 1966); Wong (1994) и Griffin (1995). Критерий Келли был применен для блэкджека Торпом (1962). Анализ более сложен, чем при бросках монеты, потому что выплаты здесь не просто один к одному. В частности дисперсия обычно больше 1, и доля Келли стремится быть меньше, чем при подбрасывании монеты с тем же самым ожиданием. Кроме того, распределение различных выплат зависит от преимуществ игрока. Например, частоты сплитов, удвоений и блэкджеков меняются по мере того, как изменяется преимущество. Задавая вероятности различных выплат в соответствии с их ожиданиями, и решая уравнения Келли на компьютере, может быть найдена стратегия, близкая к оптимальной с любой степенью точности.
Существуют некоторые заслуживающие внимания концептуальные тонкости. Чтобы показать их, мы упростим нашу модель до модели броска монеты.
При каждой попытке мы имеем "благоприятную ситуацию" с вероятностью 0.5 при выигрыше или потере X единиц на единицу ставки, так что P (X= 1) =0.51, P (X=-1)=0.49,и с вероятностью 0.5 неблагоприятную ситуацию с выигрышем или потерей Y на единицу ставки, так что P (Y= 1)=0.49 и P (Y=-1) = 0.51. Прежде, чем ставить, мы знаем, применяется X или Y.
Предположим, игрок должен делать маленькие "ждущие" ставки в неблагоприятных ситуациях, чтобы позднее иметь возможность использовать благоприятные ситуации. На них он разместит "большие" ставки. Мы рассмотрим два случая.
Случай 1. Ставим fo в неблагоприятных ситуациях и находим оптимальное f * для благоприятных ситуаций. Мы имеем
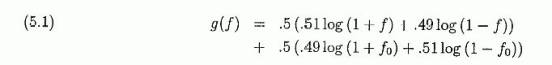
Так как второе выражение в (5.1) постоянно, f максимизирует g(f), если максимизировано первое выражение, так что f* =pi - qi= 0.02, как обычно. Легко проверить что на всем спектре благоприятных ситуаций работает тот же самый рецепт, f*i =pi - qi для i-той ситуации. Кроме этого, в реальном блэкджеке значение f*i было бы пересмотрено в меньшую сторону отчасти из-за большей дисперсии. С дополнительным ограничением типа fi ≤ kfo, где k обычно интегральный множитель для fo выражающий спред ставки, принятый благоразумным игроком, решением будет просто: fi ≤ min (f*i kfo).
Любопытно, внешне подобная формулировка проблемы ставок ведет к довольно разнящимся результатам.
Случай 2. Ставка f в благоприятных ситуациях и af в неблагоприятных ситуациях, 0 ≤ a ≤ 1 .
Теперь размеры ставки в этих двух ситуациях связаны, анализ и результаты становятся более сложными. Мы имеем норму роста Келли
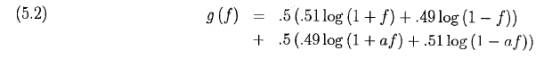
Если мы выбираем=0 (никаких ставок в неблагоприятных ситуациях), то максимальная величина g(f) будет около f* =0.02, обычная доля Келли.
Если мы делаем "ожидающие ставки" величиной a > 0, то это сместит значение f* вниз, возможно, даже до 0. Ожидаемый рост, деленный на ожидаемую ставку равен 0.02 (1 - a) / (1 + a), a ≥ 0. Если a =0, мы получим 0.02, как и ожидалось. Если а=1, мы получаем 0, как ожидалось: это - справедливая игра, и доля Келли будет f* =0. При увеличении а от 0 до 1 доля Келли (оптимальная) f* уменьшается от 0.02 до 0. Таким образом, доля Келли для благоприятных ситуаций меньше в этом случае, когда ставки при неблагоприятных ситуациях уменьшают общую выгодность игры.
Arnold Snyder обратил мое внимание на тот факт, что Winston Yamashita (также) сделал это наблюдение (18 марта 1997) на страницах вебсайта Станфорда Вонга (Stanford Wong).
В этом примере мы находим новое значение f* для данной величины a, 0 < a < 1, решая g' (f)=0. Значение a=1/3, к примеру, соответствует ставке 1/3 единицы при Y и 1 единице при X, диапазон ставок от 3 до 1. Полное ожидание будет 0.01. Вычисления дают f*=0.012001. Таблица 5.1 показывает, как f* меняется в зависимости от a.
Таблица 5.1Изменения f* от a

Чтобы понять, почему Случай 1 и Случай 2 имеет различные f*, взглянем сначала на уравнение (5.1). Часть g(f) соответствующая неблагоприятным ситуациям, фиксирована, когда фиксировано f0. Только та часть g(f), которая соответствует благоприятным ситуациям, меняется с изменением f. Таким образом, мы максимизируем g(f) только для благоприятных ситуаций. Независимо от значения f g(f) уменьшается на фиксированное количество части содержащей f0. С другой стороны, в уравнении (5.2) обе части g(f) изменяются при изменении f, потому что доля af, используемая для неблагоприятных ситуаций, находится в пропорциональной зависимости скоэффициентом а от доли f, используемой в благоприятных ситуациях. Теперь первый член, для благоприятных ситуаций, имеет максимум на f= 0.02, и приблизительно "плоский" около. Но второй элемент, для неблагоприятных ситуаций, является отрицательным и уменьшается довольно быстро при f=0.02. Поэтому, когда мы несколько уменьшаем f, этот член несколько увеличивается, в то время как первый член уменьшается лишь очень незначительно. Здесь лежит чистая выгода, так что мы находим f* < 0.02. Чем больше a, тем сильнее эффект этого слагаемого, тем сильнее мы должны уменьшить f чтобы получить f *, что ясно показано в Таблице 5.1. Когда существует спектр благоприятных ситуаций, решение более сложно и может быть найдено через стандартные многомерных методов оптимизации.
Более сложный Случай 2 соответствует тому, что серьезному игроку в блэкджек, вероятно, нужно будет делать практически. Он должен будет ограничить размер своей текущей максимальной ставки до нескольких текущих минимальных ставок. По мере того, как его капитал будет расти или уменьшаться, соответственно пропорционально увеличиваются или уменьшаются и размеры ставки.
Спортивные тотализаторы
В 1993 году выдающийся молодой доктор наук в области компьютеров рассказал мне о разработанной им успешной системе ставок в спортивном тотализаторе. После рассмотрения его системы я был убежден в его правоте. Я внес предложения для небольших упрощений и улучшений. Тогда мы согласились на полевое испытание. Мы нашли человека, который наверняка считался бы новичком среди других игроков.
Я вложил на тестовый счет $50000 и мы использовали систему Кэлли для оценки размера нашей ставки.
Мы делали ставки на протяжении 101 дня в течение первых четырёх с половиной месяцев 1994 года. Система работала на различных видах спорта. Результаты представлены на рисунках 3 и 4. После 101 дня ставок, наш счет величиной $50000 дал прибыль в $123000, около $68000 со ставок на состязания первого вида спорта и около $55000 от ставок на другой вид спорта. Ожидаемый доходы были около $62000 со ставок на состязания 1 вида спорта и около $27000 со ставок на другой вид спорта. Это может означать, что дополнительные $34000 в действительности выиграны благодаря удаче. Но, вероятно, результат является большей частью правдоподобным, так как наши ожидаемые оценки, полученные из модели, были сознательно выбраны консервативными. Причиной этому послужил тот факт, что использование слишком большого значения f* и чрезмерных ставок наказывается гораздо более жестко, чем использование слишком малого f* и низких ставок.
Хотя, $123000 – скромная сумма для некоторых, и незначительная по стандартам Wall Street, система работала как предсказывалось и прошла тест. Мы никогда не были позади более чем на несколько тысяч. Максимум, с которым мы «посягнули» на наш счет, чтобы сделать ставки, был около $10000.
Наше обычное ожидание было около 6%, таким образом общая величина наших ставок (“действий”) была около $2000000 или около $20000 в день. Мы обычно делали от пяти до пятнадцати ставок в день с разбросом от нескольких сотен долларов до нескольких тысяч каждая, возрастающих с ростом нашего счета.
Хотя мы добились чистой победы, общий результат изменялся под воздействием случайности от солидного проигрыша до большого выигрыша. Особенно трудная цель была «sawdust joint» у Little Caesar’s. Он “выдыхылся” к концу нашего теста, и я подозреваю, что потери по спортивным ставкам для нас могут ускорить его уход.
Одна из особенностей ставок на тотализаторе, которая интересна пользователям критерия Кэлли, - возможность исследования системы ставок для нескольких игр одновременно. Это также возникает в блекджеке, когда а) ставки игрока в нескольких сдачах одновременно б) два или более игроков делят один общий счет. Стандартные техники быстро решают эти проблемы. Мы иллюстрируем это примерами:
Пример 6.1. Предположим мы делаем ставки одновременно в двух независимых играх с положительным ожиданием, представляющих собой подбрасывание монеты, с долями f1 и f2, а также с вероятностями успеха p1 и p2 соответственно. Тогда ожидаемый уровень роста определяется как
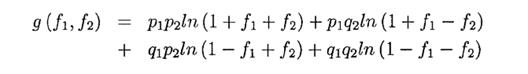
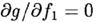 |
Для нахождения оптимальных f1 *и f2* мы решаем одновременные уравнения
и
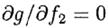 |
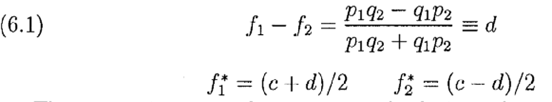
Результат будет следующим :
Эти уравнения проходят проверку на симметричность: перестановка 1 и 2 на протяжении всех преобразований переводит уравнение в себя.
Альтернативная форма поучительна. Возьмем mi=pi-qi, I=1,2; отсюда pi=(1+mi)/2 и qi=(1-mi)/2. Замена в (6.1) и упрощения приводят к:
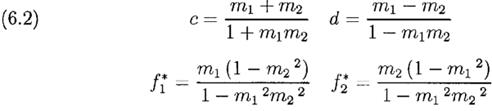 |
что явно дает множители, на величину которых fi* уменьшаются в зависимости от mi*.
Так как mi обычно несколько процентов, уменьшающие множители обычно очень близки к 1.
Рассмотрим частный случай, когда p1 =p2=p, d=0 и f * = f1* = f2* = с/2=(p-q)/(2(p2+q2)). Полагая m = p-q это может быть записано f * = m/(1+m2) для оптимальной доли ставок на обе монеты одновременно, по сравнению с f * = m для ставки на каждую монету последовательно.
Наши одновременные ставки на тотализаторе были в основном на разные виды соревнований и обычно немногочисленны, таким образом, они были приблизительно независимы и назначенные доли были только слегка меньше, чем соответствующие доли для одиночных игр. Вопрос: всегда ли это является истинным для независимых одновременных ставок? Одновременные ставки в блэкджеке на различных столах независимы, но на одном столе они имеют парные корреляции, которые были оценены на уровне 0,5 (Griffin, 1995, p.142). Это вызывает существенное уменьшение доли Кэлли в расчете на каждую сдачу. В литература по блэкджеку обсуждается подходы к решения этих проблем. С другой стороны, корреляции между доходами по ценным бумагам могут изменяться от почти –1 до почти 1. Предельные значения корреляции часто могут быть использованы для получения больших преимуществ через технику «хеджирования».
Не склонный к риску инвестор может получить такую комбинацию из ценных бумаг, при которой ожидаемый доход увеличивается, а риск имеет тенденцию к снижению. Оптимальная доля ставок может быть очень большой.
Следующий пример – простая иллюстрация важного эффекта ковариации для оптимальной доли ставки.
Пример 6.2 Мы имеем две игры с подбрасыванием монеты как и в прошлом примере, но теперь на них не накладывается ограничение на независимость их исходов. Для простоты возьмем частный случай, когда две ставки имеют одинаковое распределение выплат, но с объединенным распределением, показанным в Таблице 6.1.
 |
ТАБЛИЦА 6.1 Объединенное распределение двух идентичных игр с положительным ожиданием с коррелированными исходами.
Тогда c+m+b = (1+m)/2, откуда b=(1-m)2-c и, следовательно, 0 £ c £ (1-m)/2.
Вычисления дают Var(Xi)=1-m2 , Cor(X1,X2) = 4c-(1-m)2 и Cor(X1,X2) = [4c-(1-m)2]/(1-m2). Симметрия распределения показывает, что g(f1,f2) достигнет максимума в точке f1 = f2 =f, т.е. нам просто нужно максимизировать g(f) = (c-m)ln(1+2f)+c ln(1-2f). Результат будет
f * = m/(2(2c+m)). Мы видим, что для фиксированного m, по мере того как c уменьшается с (1-m)/2 при Cor(X1,X2) =1 до 0 при Cor(X1,X2) = -(1-m)/(1+m), f * для каждой ставки увеличивается с m/2 до ½ , как показано в Таблице 6.2.
ТАБЛИЦА 6.2 Увеличение f * при уменьшении Cor(X1,X2)
 |
Важно отметить, что для точного решения или произвольной численной аппроксимации задачи одновременных ставок недостаточно знать только ковариации или корреляции. Для построения функции g нам необходимо полное объединенное распределение.
Мы прекратили делать ставки на спортивном тотализаторе после нашего успешного теста по следующим причинам: (1) Это требует постоянного присутствия человека в штате Невада. (2) Крупные суммы наличности и большое количество выигрышных билетов должны перевозиться между игорными домами. Мы полагаем, это очень рискованно. К сожалению, последующие события подтвердили эти опасения. (3) Это занятие не выдерживало конкуренции с другими нашими операциями в экономическом плане.
Если будет возможным делать ставки по телефону из-за пределов штата и передавать соответствующие средства электронным способом, мы можем вернуться.
Заключение
Те частные лица и организации, которые заинтересованы в долгосрочном инвестировании, должны рассмотреть возможность использования критерия Кэлли для асимптотической максимизации ожидаемого сложнопроцентного уровня роста их капитала. Инвесторы с меньшей толерантностью к риску внутри периода инвестирования могут предпочесть использовать функцию с меньшими результатами (to use lesser function). Долгосрочным инвесторам целесообразно избегать использования чрезмерно большой доли («чрезмерных ставок»). Поэтому, сверх того, в соответствии со степенью неопределённости будущих вероятностей долгосрочным инвесторам следует ограничивать их инвестиционные доли (investment fraction) до достаточного предела для предотвращения значительного риска, связанного с чрезмерными ставками.
Благодарности. Я благодарю доктора Jarry Baesel, профессора Sid Browne, профессора Peter Griffin, доктора Art Quaife, а также Don Schlesinger за комментарии и исправления, и ещё Richard Reid за опубликования этой работы на его вебсайте. Я также признателен доктору Art Quaife за предоставление мне возможности использования результатов его анализа в качестве примера.
Эта работа была пересмотрена и расширена после её презентации на 10-ой Международной Конференции по Азартным Играм и Принятию Риска.
Таблица 8.3 Результаты: То, что XYZ Corp. сделала на самом деле.
| 8/17/97 | 10/9/97 | 10/9/97 | 2/9/96 | 2/9/98 | 3/31/98 | |
| Прошло лет c 8/17/97 | 0.00 | 0.15 | 0.15 | 0.48 | 0.48 | 0.62 |
| Бумага | ||||||
| Berkshire | 41,300.00 | 45,600.00 | 45,600.00 | 53,450.00 | 53,450.00 | 67,200.00 |
| BioTlme | 8.75 | 22.75 | 22.75 | 12.88 | 12.88 | 14.25 |
| T-bllls | ||||||
| Всего: | ||||||
| Первоначально | Обновление | Обновление | ||||
| Инвестиции | Инвестиции | Инвестиции | Инвестиции | Инвестиции | Инвестиции | |
| Berkshire | 209,500 | 228,000 | 228,000 | 267,250 | 801,750 | 1,008,000 |
| BioTime | 581,543 | 1,512,011 | 1,102,511 | 623.948 | 623,948 | 690,584 |
| T-bills | 289.694 | 291.381 | 700,881 | 710,393 | 175.893 | 176.859 |
| Total: | 1,080,736 | 2,031.392 | 2,031,392 | 1.601,591 | 1,601,591 | 1,875.443 |
| Увеличение с 8/17/97 | 950,656 | 950,656 | 520,855 | 520,855 | 794,706 | |
| Доля | Доля | Доля | Доля | Доля | Доля | |
| Berkshire | 0.19 | 0.11 | 0.11 | 0.17 | 0.50 | 0.54 |
| Biotime | 0.54 | 0.74 | 0.54 | 0.39 | 0.39 | 0.37 |
| T-bills | 0.27 | 0.14 | 035 | 0.44 | O.11 | 0.09 |
| Total: | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Объем | Объем | Объем | Объем | Объем | Объем | |
| Berkshire | ||||||
| BioTime | 66,462 | 66,462 | 48,462 | 48,462 | 48,462 |
Таблица 8.4 Результаты: Если бы XYZ Corp. следовала рекомендациям Quaife.
| Начало | Без «перетряски» | Одна «перетряска» | ||||
| 8/17/97 | 8/17/97 | 3/31/98 | 10/6/97 | 10/6/97 | 3/31/98 | |
| Прошло лет c 8/17/97 | 0.00 | 0.00 | 0.62 | 0.14 | 0.14 | 0.62 |
| Бумага | ||||||
| Berkshire | 41,900.00 | 41,900.00 | 67,200.00 | 46,100.00 | 46,100.00 | 67,200.00 |
| BioTime | 8.75 | 8.75 | 14.25 | 25.33 | 25.33 | 14.25 |
| T-bills | ||||||
| Total: | ||||||
| Первоначально | Баланс | Перетряска | ||||
| Инвестиции | Инвестиции | Инвестиции | Инвестиции | Инвестиции | Инвестиции | |
| Berkshire | 209,500 | 1,621,104 | 2,599,957 | 1,783,603 | 3.385.420 | 4.934,929 |
| BioTime | 581,543 | 540,368 | 880,028 | 1 ,564,494 | 1,128,473 | 634,766 |
| T-bills | 289.694 | -1.080.736 | -1.128.608 | 1. 091. 149 | -2.256.947 | -2.334,427 |
| Total: | 1,080,736 | 1,080,736 | 2,351,377 | 2,256,947 | 2,256,947 | 3,235,269 |
| Увеличение с 8/17/97 | 1,270,641 | 1,176,210 | 1,176,210 | 2,154,532 | ||
| Превышения над суботимальной стратегией совета директоров | ||||||
| 475.935 | 1,359.826 | |||||
| Оптимум | ||||||
| Доля | Доля | Доля | Доля | Доля | Доля | |
| Berkshire | 0.19 | 1.50 | 1.11 | 0.79 | 1.50 | 1.53 |
| Biotime | 0.54 | 0.50 | 0.37 | 0.69 | 0.50 | 0.20 |
| T-bills | 0.27 | -1.00 | -0.48 | -0.48 | -1.00 | -0.72 |
| Total: | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Объем | Объем | Объем | Объем | Объем | Объем | |
| Berkshire | ||||||
| BioTime | 66,462 | 61,756 | 61,756 | 61,756 | 44,545 | 44,545 |
Рисунки
