Признаки сравнения для рядов с положительными членами.
Существуют два признака сравнения, один из них называют просто признаком сравнения, другой – предельным признаком сравнения.
Сначала рассмотрим признак сравнения. На практике он встречается довольно редко, но тем не менее рассмотрим на примере.
Признак сравнения:Пусть для членов рядов 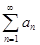 и
и 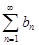 выполнено условие:
выполнено условие: 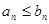 (вообще говоря, для всех
(вообще говоря, для всех 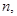 начиная с какого-то номера), тогда:
начиная с какого-то номера), тогда:
а) если ряд с бОльшими членами сходится, то и ряд с меньшими членами сходится;
б) если ряд с меньшими членами расходится, то и ряд с бОльшими членами расходится.
!!! Для использования признаков сравнения понадобиться понятие «эталонных» рядов – ряд, с которым сравнивается исследуемый ряд.
Наиболее часто используемые «эталонные» ряды:
- 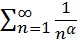 (при
(при 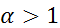 он сходится, при
он сходится, при  он расходится) – обобщенный гармонический ряд;
он расходится) – обобщенный гармонический ряд;
- 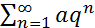 (при
(при 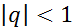 он сходится, при
он сходится, при 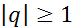 он расходится) – геометрический ряд.
он расходится) – геометрический ряд.
Пример: Исследовать ряд на сходимость 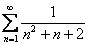
Решение: Заглядываем в «пачку» обобщенного гармонического ряда и находим похожий ряд: 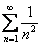 Из теории известно, что он сходится. Теперь нам нужно показать, что для всех значений
Из теории известно, что он сходится. Теперь нам нужно показать, что для всех значений 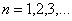 справедливо неравенство
справедливо неравенство 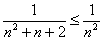 .
.
Если 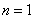 , то
, то 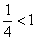
Если 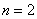 , то
, то 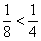
Если 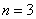 , то
, то 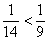
Если 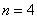 , то
, то 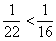
….
И так далее.
Оформить решение можно так:
Сравним исследуемый ряд со сходящимся рядом 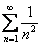 . Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство
. Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство 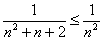 , значит, по признаку сравнения исследуемый ряд сходится вместе с рядом
, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом 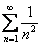 .
.
!!! Проанализируем признак сравнения и решенный пример с неформальной точки зрения. Все-таки, почему ряд 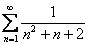 сходится? А вот почему. Если ряд
сходится? А вот почему. Если ряд 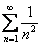 сходится, то он имеет некоторую конечную сумму
сходится, то он имеет некоторую конечную сумму 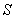 :
: 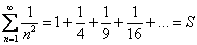 . И поскольку все члены ряда
. И поскольку все члены ряда 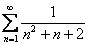 меньше соответствующих членов ряда
меньше соответствующих членов ряда 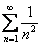 , то сумма ряда
, то сумма ряда 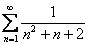 не может быть больше числа
не может быть больше числа 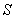 , и тем более, не может равняться бесконечности!
, и тем более, не может равняться бесконечности!
Аналогично можно доказать сходимость «похожих» рядов: 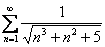 ,
, 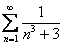 ,
, 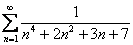 и т.д.
и т.д.
!!! Как уже отмечалось, на практике только что рассмотренный признак сравнения применяют редко. Настоящей «рабочей лошадкой» числовых рядов является предельный признак сравнения, и по частоте использования с ним может конкурировать разве что признак Даламбера.
Предельный признак сравнения:
Рассмотрим два положительных числовых ряда 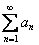 и
и 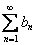 . Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу
. Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу 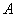 :
: 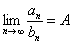 , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.
!!! Когда применяется предельный признак сравнения?Предельный признак сравнения применяется тогда, когда «начинкой» ряда у нас являются многочлены. Либо один многочлен в знаменателе, либо многочлены и в числителе и в знаменателе. Один или оба многочлена также могут находиться под корнем.
Пример: Исследовать ряд на сходимость 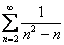
Решение: Сравним данный ряд со сходящимся рядом 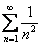 . Используем предельный признак сравнения. Известно, что ряд
. Используем предельный признак сравнения. Известно, что ряд 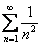 – сходится. Если нам удастся показать, что
– сходится. Если нам удастся показать, что 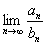 равен конечному, отличному от нуля числу, то будет доказано, что ряд
равен конечному, отличному от нуля числу, то будет доказано, что ряд 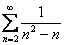 – тоже сходится.
– тоже сходится.
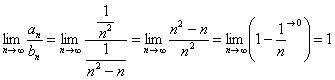
Получено конечное, отличное от нуля число, значит, исследуемый ряд сходится вместе с рядом 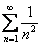 .
.
Почему для сравнения был выбран именно ряд 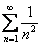 ? Если бы мы выбрали любой другой ряд из «обоймы» обобщенного гармонического ряда, то у нас не получилось бы в пределе конечного, отличного от нуля числа (можете поэкспериментировать).
? Если бы мы выбрали любой другой ряд из «обоймы» обобщенного гармонического ряда, то у нас не получилось бы в пределе конечного, отличного от нуля числа (можете поэкспериментировать).
!!! Примечание: когда мы используем предельный признак сравнения, не имеет значения, в каком порядке составлять отношение общих членов, в рассмотренном примере отношение можно было составить наоборот: 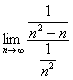 – это не изменило бы сути дела.
– это не изменило бы сути дела.
Предельный признак сравнения применим почти для всех рядов, которые мы рассмотрели в предыдущем пункте:
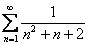 ,
, 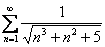 ,
, 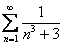 ,
, 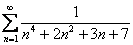 .
.
Данные ряды по только что рассмотренной трафаретной схеме нужно предельно сравнить соответственно со сходящимися рядами:
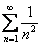 ,
, 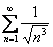 ,
, 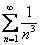 ,
, 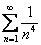 .
.
Признак сходимости Даламбера.
Радикальный признак сходимости Коши.
Интегральный признак сходимости Коши.
Одним из распространенных признаков сравнения, который встречается в практических примерах, является признак Даламбера. Признаки Коши встречаются реже, но тоже весьма популярны.
