Сходимость рядов с положительными членами

Определение. Числовой ряд называется рядом с положительными членами, если все его члены неотрицательны.

Теорема 5 (признак сравнения). Пусть даны два ряда с положительными членами:

(u) 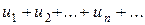, (v) ,

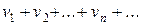причём члены ряда (u) не больше соответствующих членов ряда (v): 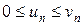, 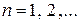. Тогда

а) если ряд (v) сходится и имеет сумму 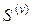, то ряд (u) также сходится, и его сумма ;

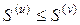б) если ряд (u) расходится, то ряд (v) также расходится.

Замечание. Теорема 5 остаётся справедливой, если неравенство 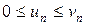выполняется, начиная с некоторого номера .

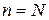Для сравнения обычно используют геометрический, гармонический и обобщённый гармонический ряды. Обобщённым гармоническим называется числовой ряд вида

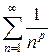, (2)

сходящийся при значениях параметра 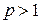и расходящийся 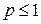при (при 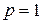он является гармоническим рядом).

Для доказательства сходимости некоторого заданного ряда с помощью признака сравнения нужно подобрать сходящийся ряд с бóльшими членами, а для доказательства расходимости – расходящийся ряд с мéньшими членами. Часто на помощь приходит теорема 1 о почленном умножении ряда на число.

Пример 6.Исследуем сходимость ряда 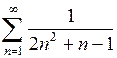. Поскольку при 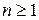справедливо неравенств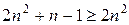о , то 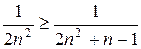. Рассмотрим ряд 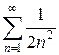. Он получен из сходящегося обобщённого гармонического ряда 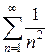умножением на 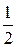и, следовательно, сходится. По части а) признака сравнения исследуемый ряд сходится.

Теорема 6 (признак Даламбера). Если для ряда 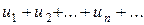со строго положительными членами ( 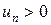) существует конечный предел 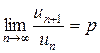, то при 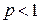данный ряд сходится, при 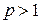– расходится.

Признак Даламбера удобно применять в тех случаях, когда общий член ряда содержит факториалы и показательные относительно номера 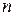функции.

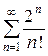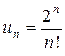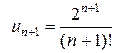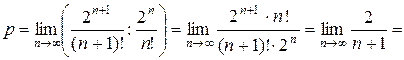
Пример 7. Исследуем сходимость ряда . Имеем: , , , 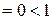поэтому ряд сходится.

Замечание 1. Если 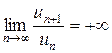, то ряд 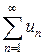расходится.

Замечание 2. Если предел 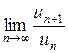равен 1 или вовсе не существует, то ряд может быть как сходящимся, так и расходящимся. Так, ряд 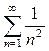сходится, а гармонический ряд 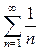расходится, хотя и в том, и в другом случае .

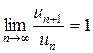Теорема 7 (радикальный признак Коши).Если для ряда 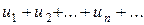с положительными членами существует конечный предел 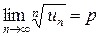, то при 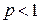данный ряд сходится, при 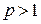– расходится.

Радикальный признак Коши удобно применять в тех случаях, когда корень 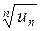извлекается.

Пример 8. Исследуем сходимость ряда .

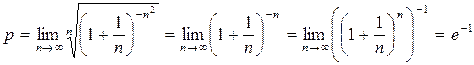. Поскольку 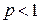, то ряд сходится.

К радикальному признаку Коши можно сделать такие же замечания 1, 2, что и к признаку Даламбера.

Теорема 8 (интегральный признак Коши). Пусть функция 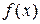непрерывна, положительна и не возрастает при 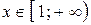. Тогда числовой ряд 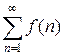сходится или расходится одновременно с несобственным интегралом .

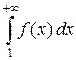С помощью интегрального признака доказывается, например, сходимость обобщённого гармонического ряда (2).

Знакопеременные ряды

Такое название носят числовые ряды, содержащие бесконечное множество как положительных, так и отрицательных членов. Частным случаем знакопеременных рядов являются знакочередующиеся ряды.

Определение. Знакочередующимсяназывается числовой ряд, у которого соседние члены имеют разные знаки.

Знакочередующийся ряд, у которого первый член положителен, обычно записывается в виде

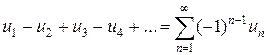, (3)

где 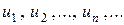– абсолютные величины членов ряда, .

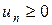Теорема 9 (признак Лейбница).Если члены знакочередующегося ряда (3) монотонно убывают по абсолютной величине: 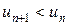, и общий член ряда стремится к нулю при 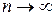: 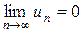, то ряд сходится, и его сумма 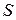удовлетворяет неравенству .

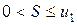Пример 9.Исследуем сходимость знакочередующегося ряда .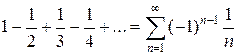

Поскольку 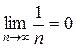и 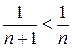для всех 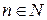, то ряд сходится, и его сумма 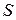удовлетворяет неравенству .

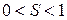Ряд, удовлетворяющий условиям теоремы 9, часто называют рядом Лейбница.

Следствие. k-ый остаток 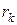ряда Лейбница имеет знак своего первого члена 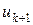и меньше его по абсолютной величине: .

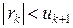Следствием пользуются при приближённых вычислениях с помощью рядов, так как оно позволяет легко определять количество слагаемых ряда (2) для приближённого вычисления его суммы. Если ряд не удовлетворяет условиям теоремы 9, сделать это значительно труднее.

Пример 10.Вычислить с погрешностью, не превосходящей 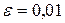, сумму ряда .

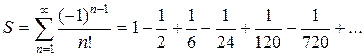Очевидно, что ряд удовлетворяет условиям теоремы 9. Поскольку у этого ряда 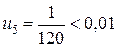, то 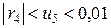. Отбросив остаток 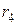из суммы ряда S, получим, что с точностью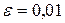

.
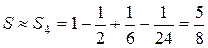