Признаки сходимости для рядов с положительными членами.

Как и в случае несобственных интегралов, важнейшим элементом теории числовых рядов является следующий: надо, не вычисляя ряда, ответить на вопрос, сходится он или нет. В конце концов, если он сходится, то его можно вычислить численно на ЭВМ, а вот если он расходится - попытки сосчитать его численно ни к чему хорошему не приведут.

В данном разделе будут

Рассмотрены признаки сходимости рядов с положительными членами. Итак, пусть даны два ряда 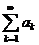и и 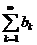выполнено условие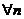 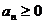и .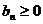

Теорема 1. Для сходимости ряда 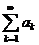необходимо и достаточно, чтобы

.

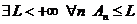Доказательство. Имеем: 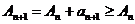и поэтому с ростом п 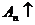. По теореме о существовании предела монотонно возрастающей последовательности, для существования конечного 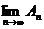необходимо и достаточно,

. <

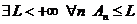Теорема 2. Пусть даны два ряда 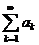(ряд А) и 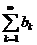(ряд В) с положительными членами и выполнено условие 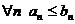. Тогда из сходимости ряда В следует сходимость ряда А, а из расходимости ряда А - расходимость ряда В.

Доказательство.

1. Пусть ряд В сходится Þ 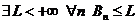. Но 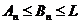Þ ряд А сходится.

2. Пусть ряд А расходится. Так как в этом случае 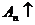, то это означает, что 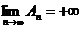. Но так как 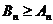, то 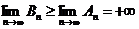и поэтому 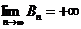и ряд В расходится. <

Замечание. Так как Отбрасывание или изменение конечногочисла членов ряда не изменяет его сходимости, то условие 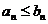может выполняться лишь .

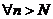Признак сходимости Коши.

Пусть существует 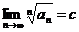. Тогда

если с < 1, то ряд 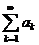сходится;

если с > 1, то ряд 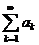расходится;

если с = 1, то вопрос о сходимости или расходимости ряда 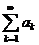не может быть решен на основании данного признака.

Этот признак сходимости носит название признака Коши.

Прежде, чем доказывать признак Коши рассмотрим ряд 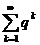, который называется геометрической прогрессией. Его частные суммы равны

.

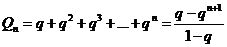Рассмотрим теперь возможные варианты.

1. Пусть 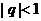. Тогда 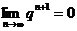и поэтому 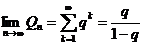и ряд 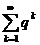сходится.

2. Пусть 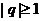. Тогда общий член ряда 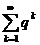не стремится к нулю и, по признаку расходимости, ряд 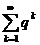расходится.

Таким образом, ряд 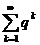сходится при 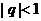и расходится при .

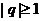А теперь

Доказательство.

Прежде всего заметим, что существование 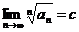означает, что

.

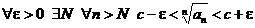А теперь - варианты.

1. Пусть 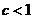. Возьмем e настолько малым, чтобы было 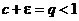. Но тогда имеем

.

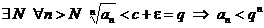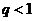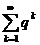Но, так как , ряд сходится, и, по теореме 2, сходится и ряд .

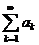2. Пусть 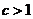. Возьмем e настолько малым, чтобы было 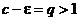. Но тогда имеем

.

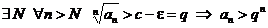Но, так как 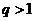, ряд 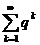расходится, и, по теореме 2, расходится и ряд . <

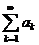Теорема 3. Если "п выполнено условие 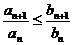, тоиз сходимости ряда В следует сходимость ряда А, а из расходимости ряда А - расходимость ряда В.

Доказательство.

Имеем следующую цепочку неравенств

; ; ; … .

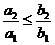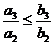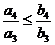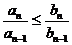Перемножая эти неравенства, получаем

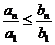, или .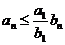

Ссылка на теорему 2 и доказывает эту теорему. <

Признак Даламбера

Пусть существует 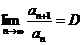. Тогда

если D < 1, то ряд 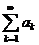сходится;

если D > 1, то ряд 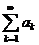расходится;

если D = 1, то вопрос о сходимости или расходимости ряда 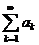не может быть рншен на основании данного признака.

Доказательство.

Прежде всего заметим, что существование 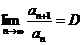означает, что

.

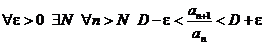1. Пусть 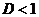. Возьмем e настолько малым, чтобы было 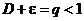. Но тогда имеем

.

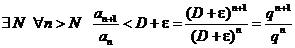Но, так как 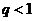, ряд 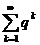сходится, и, по теореме 3, сходится и ряд .

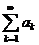2. . Пусть 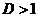. Возьмем e настолько малым, чтобы было 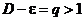. Но тогда имеем

.

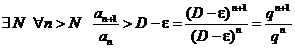Но, так как 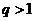, ряд 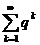расходится, и, по теореме 3, расходится и ряд . <

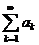Теорема 4. Пусть существует 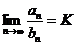и 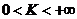. Тогда ряды 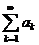и 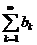сходятся или расходятся одновременно.

Доказательство.

1. Прежде всего отметим, что существование 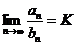означает, что

.

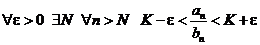2. Пусть ряд 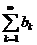сходится. Но тогда ряд 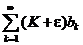также сходится, и, так как 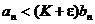, то, по теореме 2, сходится и ряд .

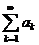3. Так как 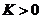, то всегда можно взять e настолько малым, чтобы было 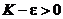. Пусть теперь ряд 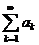сходится. Но тогда сходится и ряд 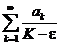и, так как 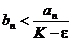, то, по теореме 2, сходится и ряд . <

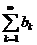Гармонический ряд

Ряд

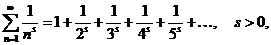
называется гармоническим рядом.

Теорема. Гармонический ряд сходится при 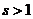и расходится при .

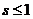Доказательство.

Рассмотрим варианты.

1. .

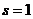В этом случае гармонический ряд принимает вид

.

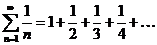Рассмотрим группу слагаемых следующего вида:

.

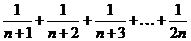Очевидно, что в этой группе всего п слагаемых и самым маленьким является последнее слагаемое. Поэтому

.

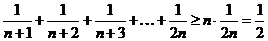Теперь в ряде 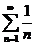сгруппируем слагаемые следующим образом

.

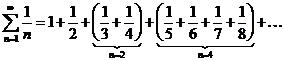Группа 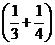соответствует п = 2, группа 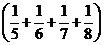- п = 4 и т.д. Но тогда

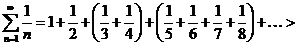
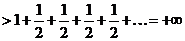
и поэтому 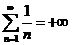, то есть ряд 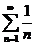расходится.

2. .

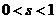Но в этом случае 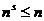, 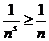и поэтому 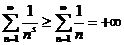, то есть 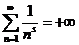, и поэтому в этом случае ряд 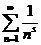расходится.

3. .

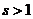В этом случае 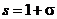и 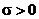. Рассмотрим группу слагаемых вида

.

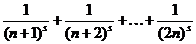В этой группе п слагаемых и каждое из них меньше 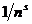. Поэтому имеем

.

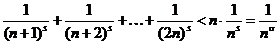Теперь сгруппируем в гармоническом ряде слагаемые в группы

.

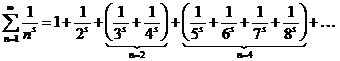Группа 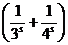соответствует п = 2 и поэтому не превосходит 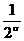; Группа 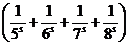соответствует п = 4 и поэтому не превосходит 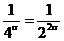; последующая группа не превосходит 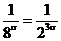и т.д.

Окончательно получим

.

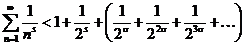Но стоящий в скобках ряд есть геометрическая прогрессия с 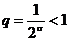; поэтому он сходится и, по теореме 2, сходится и ряд . <

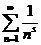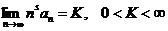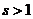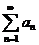Следствие. Пусть существует . Тогда при ряд сходится, а при 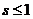- расходится.

Доказательство. Рассмотрим ряд 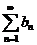с 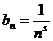. Тогда 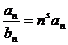при выполнении условия 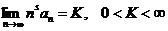сходятся или расходятся одновременно (см. теорему 4). <

Заметим, что это не означает, что сходимость любого ряда можно выяснить с помощью этого признака. Например, для ряда 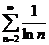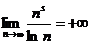при любом 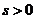и следствие не работает.