Исследование функций и построение их графиков
Найти интервалы возрастания и убывания функции:
307. 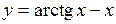 . . | 308. 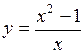 . . |
309. 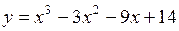 . . | 310. 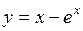 . . |
Найти точки экстремума функции:
311. 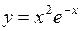 . 312.
. 312. 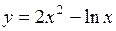 .
.
313. 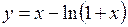 . 314.
. 314. 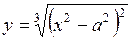 ,
, 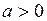 .
.
Найти интервалы выпуклости и вогнутости функции:
315. 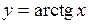 . 316.
. 316. 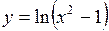 .
.
317. 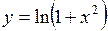 . 318.
. 318. 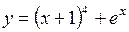 .
.
Найти точки перегиба функции:
319. 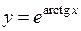 . . | 320. 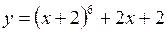 . . |
321. 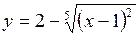 . . | 322. 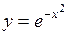 . . |
Найти асимптоты линий:
323. 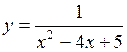 . 324.
. 324. 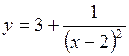 .
.
325. 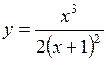 . 326.
. 326. 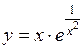 .
.
Провести полное исследование функций и построить их графики:
327. 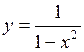 . 328.
. 328. 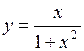 . 329.
. 329. 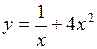 . 330.
. 330. 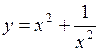 .
.
331. 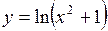 . 332.
. 332. 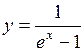 . 333.
. 333. 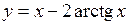 .
.
334. 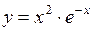 . 335.
. 335. 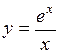 . 336.
. 336. 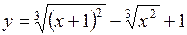 .
.
Построить схематично график непрерывной функции на интервале 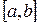 , если
, если
337. 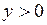 , , 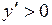 , , 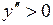 . . | 338. 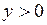 , , 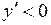 , , 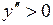 . . |
339. 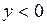 , , 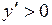 , , 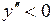 . . | 340. 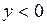 , , 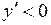 , , 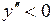 . . |
341.-343. Функция 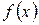 непрерывна, дан график
непрерывна, дан график 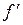 . Сколько точек экстремума у этой функции?
. Сколько точек экстремума у этой функции?
341. 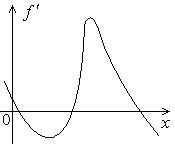 | 342. 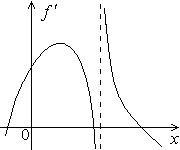 | 343. 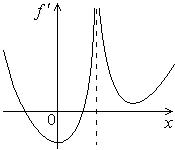 |
344.-346. Функция 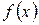 непрерывна, дан график
непрерывна, дан график 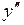 . Сколько точек перегиба у этой функции?
. Сколько точек перегиба у этой функции?
344. 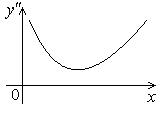 | 345. 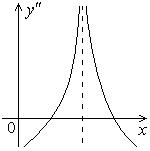 | 346. 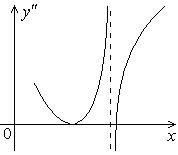 |
Ответы.307. Функция убывает при 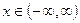 . 308. Функция возрастает при
. 308. Функция возрастает при 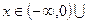
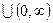 . 309. Функция возрастает при
. 309. Функция возрастает при 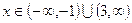 , функция убывает при
, функция убывает при 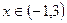 .
.
310. Функция возрастает при 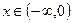 , функция убывает при
, функция убывает при 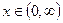 . 311.
. 311. 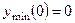 ,
,
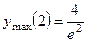 . 312.
. 312. 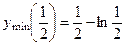 . 313.
. 313. 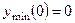 . 314.
. 314. 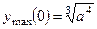 ,
, 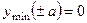 .
.
315. Функция вогнута при 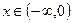 , функция выпукла при
, функция выпукла при 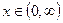 . 316. Функция
. 316. Функция
выпукла при 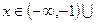
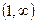 . 317. Функция выпукла при
. 317. Функция выпукла при 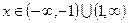 , функция
, функция
вогнута при 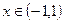 . 318. Функция вогнута при
. 318. Функция вогнута при 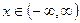 . 319.
. 319. 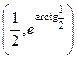 .
.
320. Точек перегиба нет. 321. Точек перегиба нет. 322. 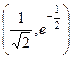 ,
, 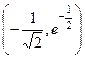 .
.
323. 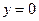 . 324. x=2, y=3. 325.
. 324. x=2, y=3. 325. 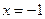 ,
, 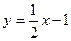 . 326.
. 326. 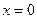 ,
, 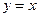 . 327. ОДЗ:
. 327. ОДЗ:
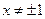 ; график симметричен относительно оси
; график симметричен относительно оси 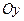 ;
; 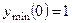 ; вертикальные асимптоты
; вертикальные асимптоты
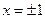 ; горизонтальная асимптота
; горизонтальная асимптота 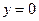 . 328. График симметричен относительно начала
. 328. График симметричен относительно начала
координат; 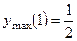 ,
, 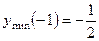 ; точки перегиба
; точки перегиба 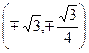 ;
; 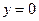 - горизонтальная
- горизонтальная
асимптота. 329. ОДЗ: 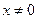 ;
; 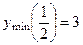 ; точка перегиба
; точка перегиба 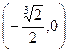 ;
; 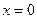 - вертикальная
- вертикальная
асимптота. 330. ОДЗ: 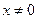 ; график симметричен относительно оси
; график симметричен относительно оси 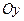 ;
; 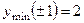 ;
;
точек перегиба нет; 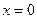 - вертикальная асимптота. 331. График симметричен относительно
- вертикальная асимптота. 331. График симметричен относительно
оси 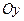 ;
; 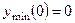 ; точки перегиба
; точки перегиба 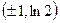 ; асимптот нет. 332. ОДЗ:
; асимптот нет. 332. ОДЗ: 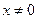 ; экстремумов
; экстремумов
нет; точек перегиба нет; вертикальная асимптота 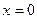 ; горизонтальные асимптоты
; горизонтальные асимптоты 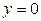 ,
,
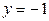 . 333. График симметричен относительно начала координат;
. 333. График симметричен относительно начала координат; 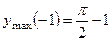 ;
;
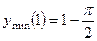 ; точка перегиба
; точка перегиба 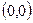 ;
; 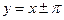 - наклонные асимптоты. 334.
- наклонные асимптоты. 334. 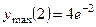 ,
,
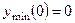 ;
; 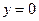 - горизонтальная асимптота; точки перегиба
- горизонтальная асимптота; точки перегиба 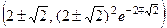 .
.
335. ОДЗ: 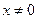 ;
; 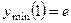 ; точек перегиба нет; вертикальная асимптота
; точек перегиба нет; вертикальная асимптота 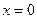 , горизонтальная асимптота
, горизонтальная асимптота 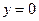 . 336.
. 336. 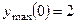 ,
, 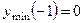 ; точка перегиба
; точка перегиба 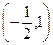 ,
,
горизонтальная асимптота 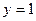 . 341. 3. 342. 4. 343. 2. 344. Нет. 345. 2. 346. 2.
. 341. 3. 342. 4. 343. 2. 344. Нет. 345. 2. 346. 2.
Функции двух переменных
Найти область определения функции и нарисовать эту область:
347. 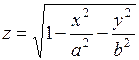 . 348.
. 348. 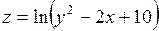 . 349.
. 349. 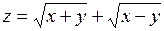 .
.
350. 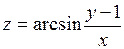 . 351.
. 351. 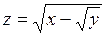 . 352.
. 352. 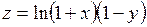 .
.
353. 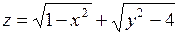 . 354.
. 354. 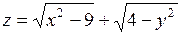 .
.
355. 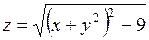 . 356.
. 356. 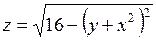 . 357.
. 357. 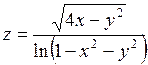 .
.
358. 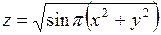 . 359.
. 359. 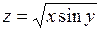 . 360.
. 360. 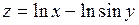 .
.
Найти частные производные первого порядка:
361. 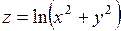 . 362. . 362. 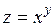 . . | 363. 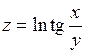 . 364. . 364. 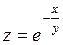 . . |
Найти все частные производные второго порядка.
365. 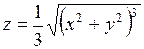 . . | 366. 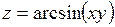 . . |
367. 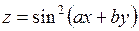 . . | 368. 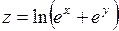 . . |
Доказать справедливость равенства:
369.если 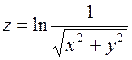 , то
, то 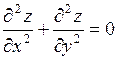 .
.
370. если 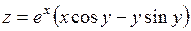 , то
, то 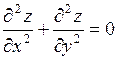 .
.
371. если 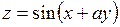 , то
, то 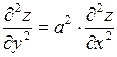 .
.
372. если 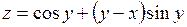 , то
, то 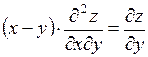 .
.
373. если 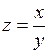 , то
, то 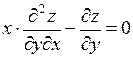 .
.
Найти 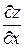 и
и 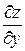 , если
, если
374. 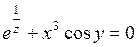 . . | 375. 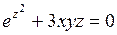 . . | 376. 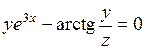 . . |
377. 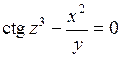 . . | 378. 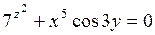 . . | 379. 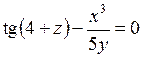 . . |
Найти полные дифференциалы функции:
380. 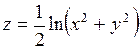 . 381.
. 381. 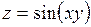 . 382.
. 382. 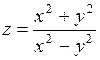 . 383.
. 383. 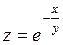 .
.
Вычислить приближенно с помощью дифференциала:
384. 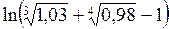 . . | 385. 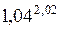 . . |
386. 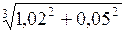 . . | 387. 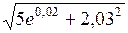 . . |
Найти уравнение касательной плоскости и нормали к поверхности:
388. 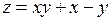 в точке в точке 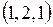 . . | 389. 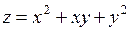 в точке в точке 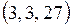 . . |
390. 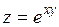 в точке в точке 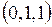 . . | 391. 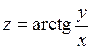 в точке в точке 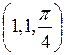 . . |
Исследовать функцию на экстремум:
392. 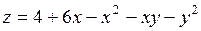 . . | 393. 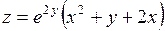 . . |
394. 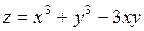 . . | 395. 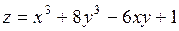 . . |
Ответы347. 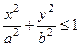 . 348.
. 348. 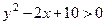 . 349.
. 349. 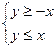 . 350.
. 350. 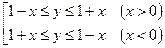 .
.
351. 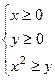 . 352.
. 352. 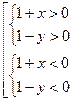 . 353.
. 353. 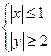 . 354.
. 354. 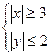 . 355.
. 355. 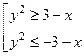 .
.
356. 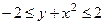 . 357.
. 357. 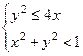 . 358. Внутренность круга
. 358. Внутренность круга 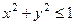 и колец
и колец
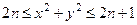 ,
, 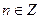 . 359.
. 359. 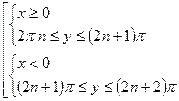 ,
, 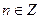 . 360.
. 360. 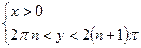 ,
,
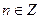 . 361.
. 361. 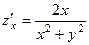 ,
, 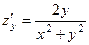 . 362.
. 362. 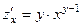 ,
, 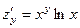 . 363.
. 363. 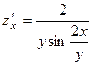 ,
,
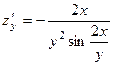 . 364.
. 364. 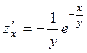 ,
, 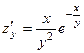 . 365.
. 365. 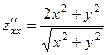 ,
, 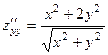 ,
,
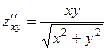 . 366.
. 366. 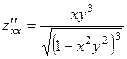 ,
,  ,
, 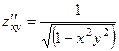 .
.
367. 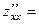
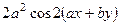 ,
, 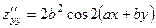 ,
, 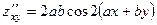 .
.
368. 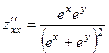 ,
, 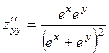 ,
, 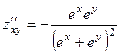 . 374.
. 374. 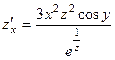 ,
,
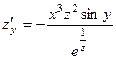 . 375.
. 375. 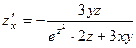 ,
, 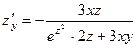 . 376.
. 376. 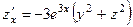 ,
,
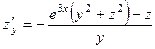 . 377.
. 377. 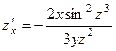 ,
, 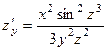 . 378.
. 378. 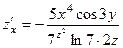 ,
,
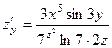 . 379.
. 379. 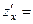
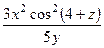 ,
, 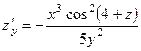 . 380.
. 380. 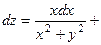
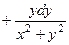 . 381.
. 381. 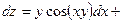
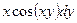 . 382.
. 382. 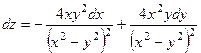 .
.
383. 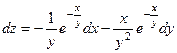 . 384.
. 384. 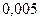 . 385.
. 385. 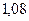 . 386.
. 386. 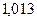 . 387.
. 387. 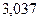 .
.
388. 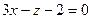 ,
, 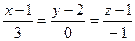 . 389.
. 389. 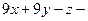
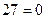 ,
, 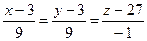 .
.
390. 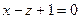 ,
, 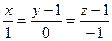 . 391.
. 391. 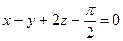 ,
, 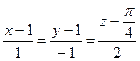 .
.
392. 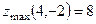 . 393.
. 393. 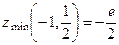 . 394.
. 394. 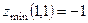 . 395.
. 395. 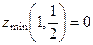 .
.
Неопределенный интеграл. Простейшие методы интегрирования
Воспользовавшись таблицей интегралов и простейшими свойствами вычислить интегралы:
396. 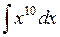 . . | 397. 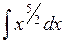 . . | 398. 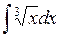 . . |
399. 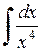 . . | 400. 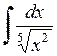 . . | 401. 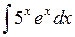 . . |
402. 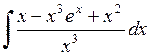 . . | 403. 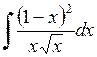 . . | 404. 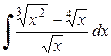 . . |
405. 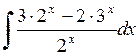 . . | 406. 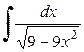 . . | 407. 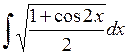 . . |
408. 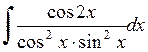 . . | 409. 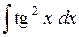 . . | 410. 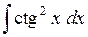 . . |
411. 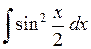 . . | 412. 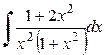 . . | 413. 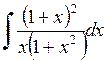 . . |
Вычислить интегралы:
414. 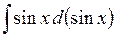 . . | 415. 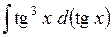 . . | 416. 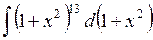 . . |
Методом подведения под дифференциал, вычислить интегралы:
417. 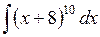 . . | 418. 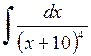 . . | 419. 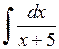 . . |
420. 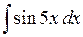 . . | 421. 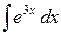 . . | 422. 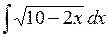 . . |
423. 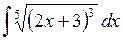 . . | 424. 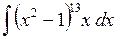 . . | 425. 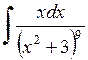 . . |
426. 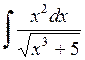 . . | 427. 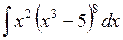 . . | 428. 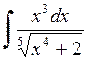 . . |
429. 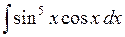 . . | 430. 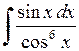 . . | 431. 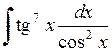 . . |
432. 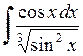 . . | 433. 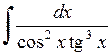 . . | 434. 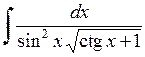 . . |
435. 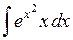 . . | 436. 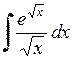 . . | 437. 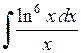 . . |
438. 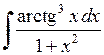 . . | 439. 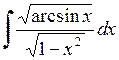 . . | 440. 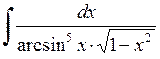 . . |
441. 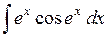 . . | 442. 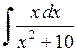 . . | 443. 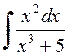 . . |
444. 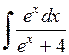 . . | 445. 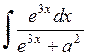 . . | 446. 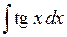 . . |
447. 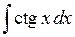 . . | 448. 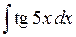 . . | 449. 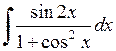 . . |
450. 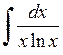 . . | 451. 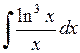 . . | 452. 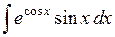 . . |
453. 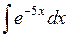 . . | 454. 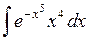 . . | 455. 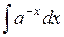 . . |
456. 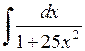 . . | 457. 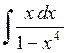 . . | 458. 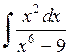 . . |
459. 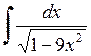 . . | 460. 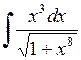 . . | 461. 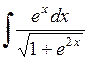 . . |
462. 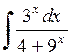 . . | 463. 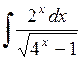 . . | 464. 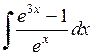 . . |
465. 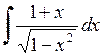 . . | 466. 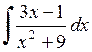 . . | 467. 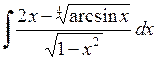 . . |
468. 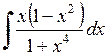 . . | 469. 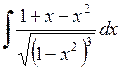 . . | 470. 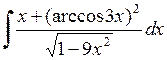 . . |
471. 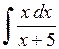 . . | 472. 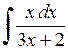 . . | 473. 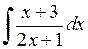 . . |
474. 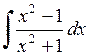 . . | 475. 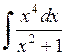 . . | 476. 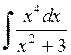 . . |
Вычислить интегралы с помощью замены переменной:
477. 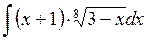 . . | 478. 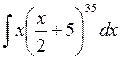 . . | 479. 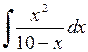 . . |
480. 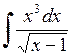 . . | 481. 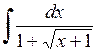 . . | 482. 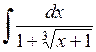 . . |
483. 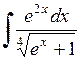 . 484.
. 484. 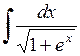 . 485.
. 485. 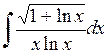 . 486.
. 486. 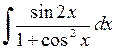 .
.
Вычислить интегралы, зависящие от квадратного трехчлена:
487. 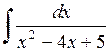 . . | 488. 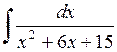 . . | 489. 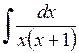 . . |
490. 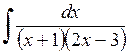 . . | 491. 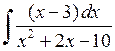 . . | 492. 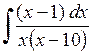 . . |
493. 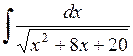 . . | 494. 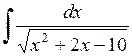 . . | 495. 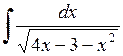 . . |
496. 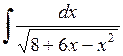 . . | 497. 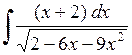 . . | 498. 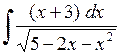 . . |
Ответы.396. 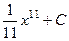 . 397.
. 397. 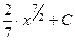 . 398.
. 398. 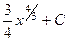 . 399.
. 399. 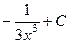 .
.
400. 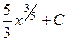 . 401.
. 401. 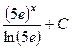 . 402.
. 402. 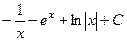 . 403.
. 403. 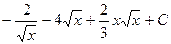 .
.
404. 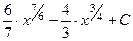 . 405.
. 405. 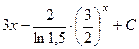 . 406.
. 406. 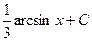 . 407.
. 407. 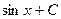 .
.
408. 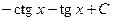 . 409.
. 409. 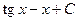 . 410.
. 410. 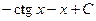 . 411.
. 411. 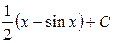 .
.
412. 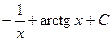 . 413.
. 413. 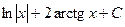 . 414.
. 414. 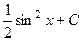 . 415.
. 415. 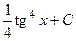 .
.
416. 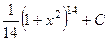 . 417.
. 417. 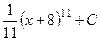 . 418.
. 418. 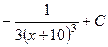 . 419.
. 419. 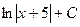 .
.
420.  . 421.
. 421. 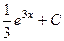 . 422.
. 422. 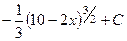 . 423.
. 423. 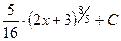 .
.
424. 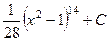 . 425.
. 425. 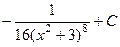 . 426.
. 426. 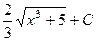 . 427.
. 427. 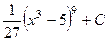 .
.
428. 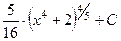 . 429.
. 429. 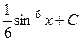 . 430.
. 430. 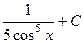 . 431.
. 431. 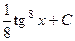 .
.
432. 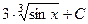 . 433.
. 433. 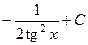 . 434.
. 434. 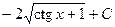 . 435.
. 435. 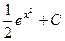 .
.
436. 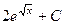 . 437.
. 437. 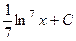 . 438.
. 438. 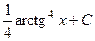 . 439.
. 439. 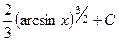 .
.
440. 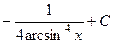 . 441.
. 441. 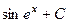 . 442.
. 442. 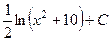 . 443.
. 443. 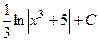 .
.
444. 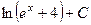 . 445.
. 445. 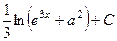 . 446.
. 446. 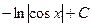 . 447.
. 447. 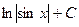 .
.
448. 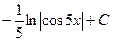 . 449.
. 449. 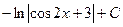 . 450.
. 450. 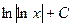 . 451.
. 451. 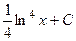 .
.
452. 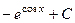 . 453.
. 453. 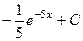 . 454.
. 454. 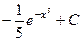 . 455.
. 455. 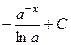 .
.
456. 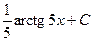 . 457.
. 457. 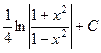 . 458.
. 458. 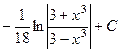 . 459.
. 459. 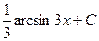 .
.
460. 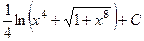 . 461.
. 461. 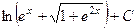 . 462.
. 462. 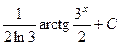 .
.
463. 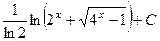 . 464.
. 464. 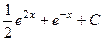 . 465.
. 465. 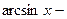
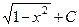 .
.
466. 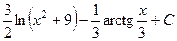 . 467.
. 467. 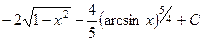 . 468.
. 468. 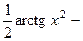
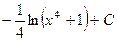 . 469.
. 469. 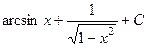 . 470.
. 470. 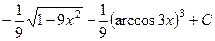 .
.
471.  . 472.
. 472. 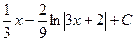 . 473.
. 473. 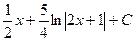 .
.
474. 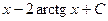 . 475.
. 475. 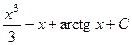 . 476.
. 476. 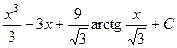 .
.
477. 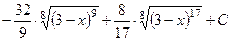 . 478.
. 478. 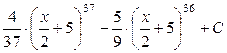 .
.
479. 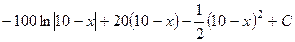 . 480.
. 480. 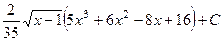 .
.
481. 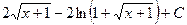 . 482.
. 482. 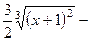
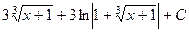 .
.
483. 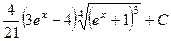 . 484.
. 484. 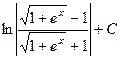 . 485.
. 485. 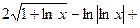
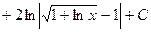 . 486.
. 486. 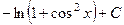 487.
487. 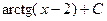 . 488.
. 488. 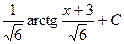 .
.
489. 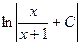 . 490.
. 490. 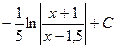 . 491.
. 491. 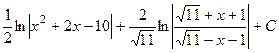 .
.
492. 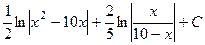 . 493.
. 493. 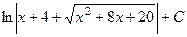 .
.
494. 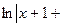
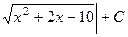 . 495.
. 495. 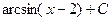 . 496.
. 496. 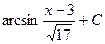 .
.
497. 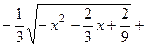
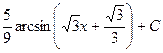 . 498.
. 498. 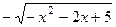
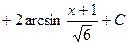 .
.
