Дифференциальное исчисление функции одной переменной. Дифференцирование неявно заданных и параметрически заданных функций. Логарифмическое дифференцирование
Производная функции, ее геометрический и физический смысл.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
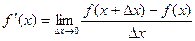
 у
у
f(x)
f(x0 +Dx) P
Df
f(x0) M
a b Dx
0 x0 x0 + Dx x
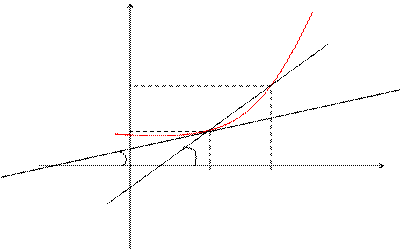
Пусть f(x) определена на некотором промежутке (a, b). Тогда 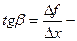 тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.

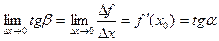 ,
,
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: 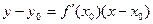

Уравнение нормали к кривой: 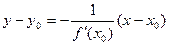 .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения 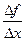 при условии, что это отношение существует.
при условии, что это отношение существует.
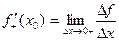
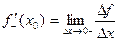
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3) 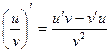 , если v ¹ 0
, если v ¹ 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С¢ = 0; 9) 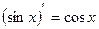
2)(xm)¢ = mxm-1; 10) 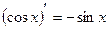
3) 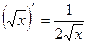 11)
11) 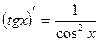
4) 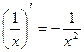 12)
12) 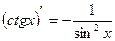
5) 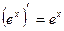 13)
13) 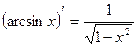
6) 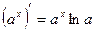 14)
14) 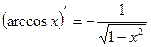
7) 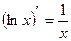 15)
15) 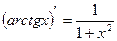
8) 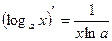 16)
16) 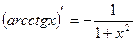
Производная сложной функции.
Теорема.Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда 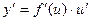
Доказательство.
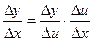
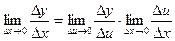
( с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)
Тогда 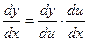
Теорема доказана.
Логарифмическое дифференцирование.
Рассмотрим функцию 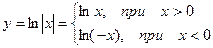 .
.
Тогда (lnïxï)¢= 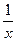 , т.к.
, т.к. 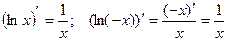 .
.

Учитывая полученный результат, можно записать 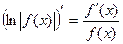 .
.
Отношение 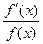 называется логарифмической производной функции f(x).
называется логарифмической производной функции f(x).
Способ логарифмического дифференцированиясостоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле

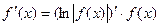
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных и показательно-степенных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Производная показательно- степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu
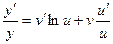
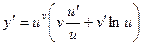

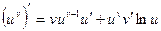
Пример. Найти производную функции 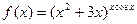 .
.
По полученной выше формуле получаем: 
Производные этих функций: 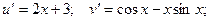
Окончательно:
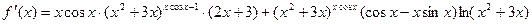
Производная обратных функций.
Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.
Для решения этой задачи дифференцируем функцию x = g(y) по х:
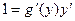
т.к. g¢(y) ¹ 0 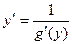

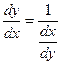
т.е. производная обратной функции обратна по величине производной данной функции.
Пример. Найти формулу для производной функции arctg.
Функция arctg является функцией, обратной функции tg, т.е. ее производная может быть найдена следующим образом:
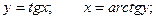
Известно, что 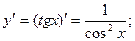
По приведенной выше формуле получаем:
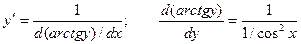
Т.к. 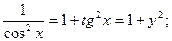 то можно записать окончательную формулу для производной арктангенса:
то можно записать окончательную формулу для производной арктангенса:
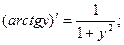
Таким образом получены все формулы для производных арксинуса, арккосинуса и других обратных функций, приведенных в таблице производных.
Производная функции, заданной параметрически.
Пусть 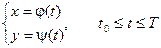
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].
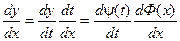
т.к. Ф(х) – обратная функция, то 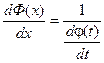
Окончательно получаем: 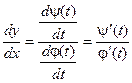
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
Пример. Найти производную функции 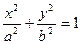
Способ 1: Выразим одну переменную через другую 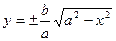 , тогда
, тогда
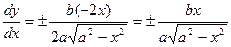
Способ 2: Применим параметрическое задание данной кривой: 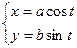 .
.
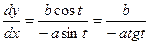
x2 = a2cos2t; 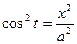
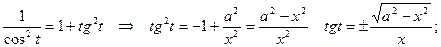
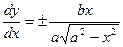
Лекция 4. Дифференциал функции одной переменной. Основные теоремы дифференциального исчисления. Применение основных теорем дифференциального исчисления.Понятие дифференциала функции. Свойства дифференциала. Геометрический смысл дифференциала. Механический смысл дифференциала. Формула Тейлора. Применение формулы Тейлора к вычислению значений функции. Применение дифференциала к приближённым вычислениям. Теоремы Ферма, Ролля, Лагранжа, Коши. Формула конечных приращений. Правило Лопиталя.
Дифференциал функции.
Пусть функция y = f(x) имеет производную в точке х:
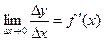
Тогда можно записать: 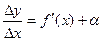 , где a®0, при Dх®0.
, где a®0, при Dх®0.
Следовательно: 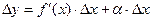 .
.
Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.
Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f¢(x)Dx или

dy = f¢(x)dx.
Можно также записать: 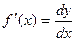
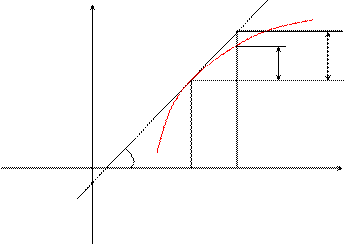
Геометрический смысл дифференциала.
 y
y
f(x)
K
dy
M Dy
L
a
x x + Dx x
Из треугольника DMKL: KL = dy = tga×Dx = y¢×Dx
Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv
2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv
3) d(Cu) = Cdu
4) 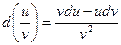
Дифференциал сложной функции.
Инвариантная форма записи дифференциала.
Пусть y = f(x), x = g(t), т.е. у - сложная функция.

Тогда dy = f¢(x)g¢(t)dt = f¢(x)dx.
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Однако, если х - независимая переменная, то
dx = Dx, но
если х зависит от t, то Dх ¹ dx.
Таким образом, форма записи dy = f¢(x)Dx не является инвариантной.
Пример. Найти производную функции 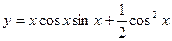 .
.
Сначала преобразуем данную функцию: 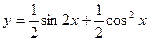
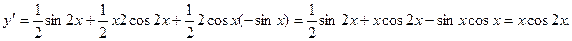
Пример. Найти производную функции 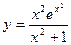 .
.
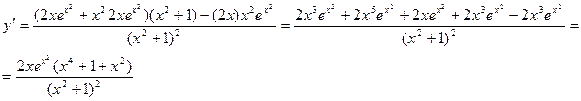
Пример. Найти производную функции 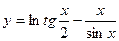
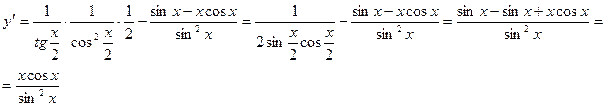
Пример. Найти производную функции 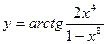
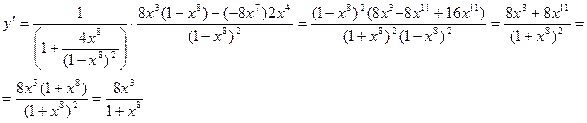
Пример. Найти производную функции 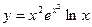
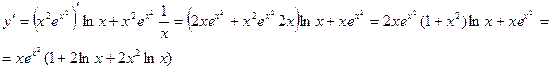
Формула Тейлора.
