Исследование функций и построение
ГРАФИКОВ
7.1. Исследование с помощью 1 – й производной.
Признак монотонности функции
ТЕОРЕМА 1 Если функция 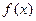 дифференцируема на
дифференцируема на
интервале 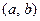 и
и 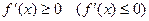 на
на
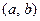 , то функция
, то функция 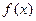 не убывает (не воз –
не убывает (не воз –
растает) на интервале 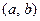 .
.
Доказательство. Возьмём две точки 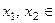
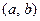 , такие что
, такие что 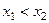 . Тогда на отрезке
. Тогда на отрезке 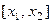 выполняются все условия теоремы Лагранжа, согласно которой получаем
выполняются все условия теоремы Лагранжа, согласно которой получаем
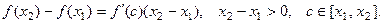
Тогда, если 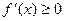 на
на 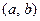 , то
, то 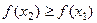 ; если
; если 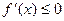 на
на 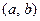 , то
, то 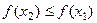 . Теорема доказана.
. Теорема доказана.
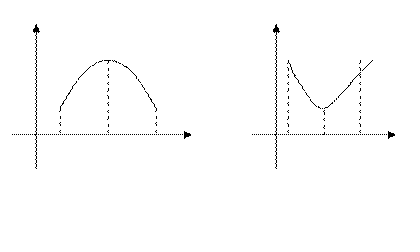
Точка  называется точкой строгого локального макси -мума (минимума) функции
называется точкой строгого локального макси -мума (минимума) функции 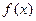 , если для всех из некоторой d - окрестности точки
, если для всех из некоторой d - окрестности точки  выполняется неравенство
выполняется неравенство 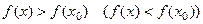 . При
. При 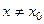 . (см. рис 1)
. (см. рис 1)
Y y
maxx
minx
O O
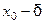

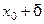
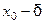

(рис. 1)
Локальный максимум ( 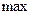 ) и локальный минимум (
) и локальный минимум ( 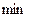 ) объединяют общим названием локальный экстремум.
) объединяют общим названием локальный экстремум.
ТЕОРЕМА 2 (необходимое условие локального экстремума)
Если функция 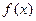 имеет в точке
имеет в точке  локаль –
локаль –
ный экстремум и дифференцируема в этой
точке, то 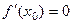 .
.
Доказательство. Так как в точке  функция
функция 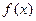 имеет ло -кальный экстремум, то существует интервал,
имеет ло -кальный экстремум, то существует интервал, 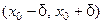 , в котором значение
, в котором значение 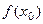 является наибольшим или наимень- шим, а тогда, по теореме Ферма, в этой точке производная равна 0., т.е.
является наибольшим или наимень- шим, а тогда, по теореме Ферма, в этой точке производная равна 0., т.е. 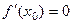 .
.
Условие 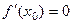 - это необходимое но не достаточное условие экстремума. Иногда точки, в которых
- это необходимое но не достаточное условие экстремума. Иногда точки, в которых 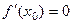 , называют критическими точками , или точками возможного экстремума функции
, называют критическими точками , или точками возможного экстремума функции 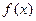 . В этих точках экстремум может быть или не быть, Например, если рассмотреть функцию
. В этих точках экстремум может быть или не быть, Например, если рассмотреть функцию 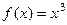 . Её производная
. Её производная 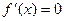 в точке
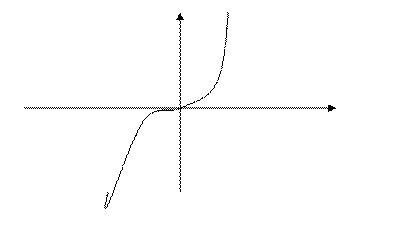
в точке 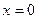 . Но по виду графика, можем определить, что в этой точке функция не имеет экстремума. (см. рис 2)
. Но по виду графика, можем определить, что в этой точке функция не имеет экстремума. (см. рис 2)
 Y
Y
· x
ЗАМЕЧАНИЕ. Если в точке  производная
производная 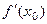 не су -щеествует, но сама точка
не су -щеествует, но сама точка  входит в область определения функции
входит в область определения функции 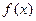 , то точка
, то точка  также является критической точ -кой функции
также является критической точ -кой функции 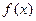 .
.
ТЕОРЕМА 3 (достаточное условие экстремума) Пусть функ-
ция 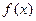 дифференцируема в некоторой d - ок –
дифференцируема в некоторой d - ок –
рестности критической точки  , тогда, если в
, тогда, если в
этой точке производная меняет знак с 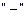 на
на
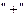 , то в точке
, то в точке  функция имеет локальный
функция имеет локальный
минимум, а если в точке  знак производной
знак производной
меняется с 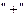 на
на 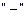 , то в точке
, то в точке  функ –
функ –
ция 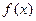 имеет локальный максимум.
имеет локальный максимум.
ПРИМЕРЫ. Построим графики функций при помощи производной 1-го порядка.
1. 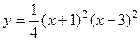 .
.
Эта функция определена для всех х, принимает она только положительные значения. 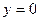 при
при 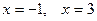 .
.
Найдём производную это1 функции:
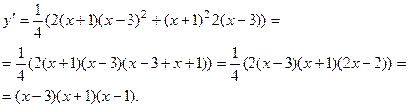
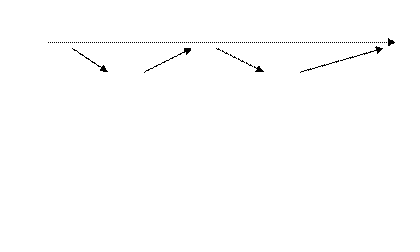
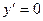 при
при 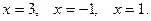 Это критические точки функции. Построим числовую ось
Это критические точки функции. Построим числовую ось
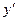 - -1 + 1 - 3 +
- -1 + 1 - 3 +
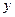
min max min
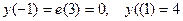 ,
, 
Исследование с помощью первой производной завершено. Мы выяснили, что график имеет две точки локального минимума и одну точку локального максимума. Нашли промежутки убывания и возрастания функции. Нашли точки пересечения с осями координат. Осталось построить график.
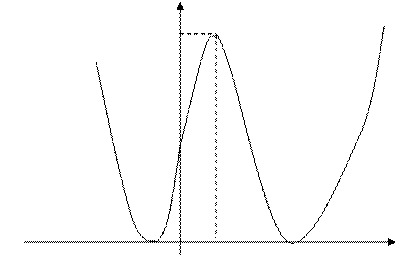 Y
Y
2,25
-1 O 1 3 x
2. 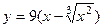 .
.
 Эта функция определена для всех
Эта функция определена для всех 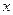 и принимает любые значения..
и принимает любые значения.. 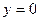 при
при 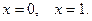 Найдём её производную:
Найдём её производную:
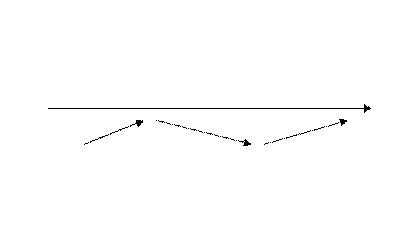
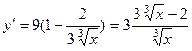 . Критическими точками являются:
. Критическими точками являются:
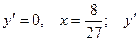 не существует,
не существует, 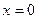 . Построим числовую ось
. Построим числовую ось
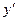 + 0 -
+ 0 - 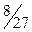 + х
+ х
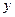
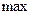
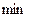
Найдём значения функции в критических точках 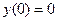 ,
,
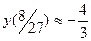 .
.
Построим график
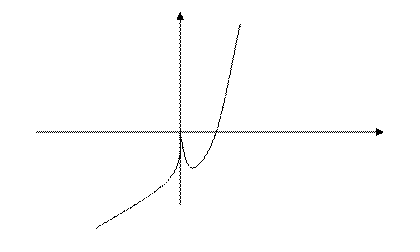
 У
У
О 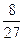 1 х
1 х
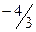
ЗАМЕЧАНИЕ. Если в точке  производная не существует, то в этой точке график функции имеет вертикальную касательную ( в случае, если точка входит в область определения)
производная не существует, то в этой точке график функции имеет вертикальную касательную ( в случае, если точка входит в область определения)
7.2. Направление выпуклости и точки перегиба графика функции.
Пусть функция  дифференцируема на интервале
дифференцируема на интервале 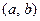 . Тогда существует касательная к графику этой функции в любой точке
. Тогда существует касательная к графику этой функции в любой точке 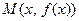 , причём эта касательная не параллельны оси
, причём эта касательная не параллельны оси 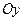 , так как её угловой коэффициент, равный
, так как её угловой коэффициент, равный 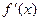 , конечен.
, конечен.
О п р е д е л е н и е 1.. Будем говорить, что график функции  имеет выпуклость, направленную вниз (или вогнутость) если расположен не ниже любой своей касательной в рассматриваемом промежутке, аналогично, график имеет выпуклость, направленную вверх (или просто выпуклость) если он находится не выше любой своей касательной. (см. рис.)
имеет выпуклость, направленную вниз (или вогнутость) если расположен не ниже любой своей касательной в рассматриваемом промежутке, аналогично, график имеет выпуклость, направленную вверх (или просто выпуклость) если он находится не выше любой своей касательной. (см. рис.)
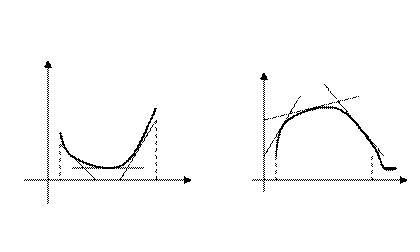
У у
Вверх
Вниз
O a b x O a b x
ТЕОРЕМА 1. Если функция  имеет на интервале
имеет на интервале
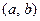 вторую производную и
вторую производную и
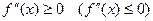 во всех точках проме –
во всех точках проме –
жутка 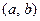 , то график функции
, то график функции  име –
име –
ет на этом промежутке выпуклость, направлен –
ную вниз (вверх).
Доказательство. Требуется показать, что график функции  находится не ниже (не выше) любой касательной, проведённой в произвольной точке
находится не ниже (не выше) любой касательной, проведённой в произвольной точке 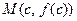 графика функции. Запишем уравнение этой касательной, обозначив её текущую ординату через
графика функции. Запишем уравнение этой касательной, обозначив её текущую ординату через 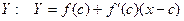 . (1)
. (1)
Напишем разложение функции  в окрестности точки
в окрестности точки 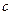 по формуле Тейлора при
по формуле Тейлора при 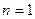
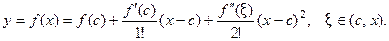 (2)
(2)
Вычитая равенство (1) из равенства (2), получим
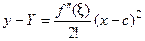 . (3)
. (3)
Тогда, если 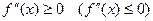 , то
, то 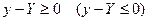 и график функции расположен не ниже (не выше) любой касательной.
и график функции расположен не ниже (не выше) любой касательной.
О п р е д е л е н и е 2. Точка 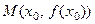 называется точкой перегиба функции
называется точкой перегиба функции  , если в точке
, если в точке  ,, если в этой точке график функции меняет направление выпуклости.
,, если в этой точке график функции меняет направление выпуклости.
ТЕОРЕМА 2 (Необходимое условие выпуклости). Пусть гра-
фик функции  имеет перегиб в точке
имеет перегиб в точке
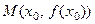 и пусть функция
и пусть функция  имеет
имеет
в точке  непрерывную вторую производную.
непрерывную вторую производную.
Тогда 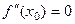 .
.
Эта теорема следует из определения точки перегиба - точке перегиба меняется направление выпуклости и вторая производная меняет знак в этой точке. А так как вторая производная непрерывна в этой точке, то она обращается в ноль в токе  ..
..
ЗАМЕЧАНИЕ 1. Если 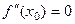 , то достаточным условием точки перегиба в точке
, то достаточным условием точки перегиба в точке  является смена знака второй производной в этой точке.
является смена знака второй производной в этой точке.
ЗАМЕЧАНИЕ 2. В точке перегиба касательная пересекает график функции, так как с одной стороны график функции находится выше касательной, а с другой - выше, т.е. перегибается через неё. (См. рис.)
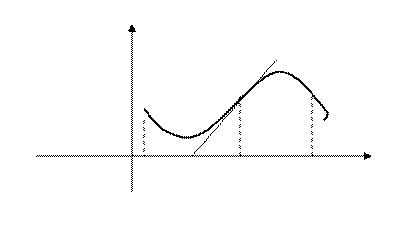
У
M
O a  b x
b x
ЗАМЕЧАНИЕ 3. Если  - точка максимума функции
- точка максимума функции  , то
, то 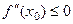 , если
, если  - точка минимума, то
- точка минимума, то 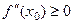 . Это ещё одно достаточное условие экстремума функции.
. Это ещё одно достаточное условие экстремума функции.
7.2. Асимптоты графика функции.
При исследовании поведения функции на бесконечности, т.е. при 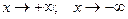 , или вблизи точек разрыва 2 – го рода часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называются асимптотами.
, или вблизи точек разрыва 2 – го рода часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называются асимптотами.
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
О п р е д е л е н и е 1. Прямая 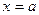 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 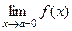 или
или 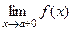 равно
равно 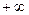 или
или 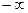 .
.
О п р е д е л е н и е 2. Прямая 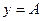 называется горизон- тальной асимптотой графика функции
называется горизон- тальной асимптотой графика функции  при
при 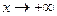 или
или 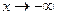 , если
, если 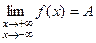 .
.
О п р е д е л е н и е 3. Прямая 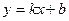 (
( 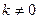 ) называ- ется наклонной асимптотой графика функции
) называ- ется наклонной асимптотой графика функции  при
при 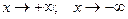 , если функцию
, если функцию 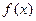 можно представить в виде
можно представить в виде 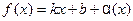 , где
, где 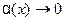 при
при 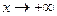 или
или 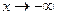 .
.
При этом числа 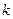 и
и 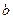 , задающие уравнение наклонной асимптоты находятся по следующим формулами:
, задающие уравнение наклонной асимптоты находятся по следующим формулами:
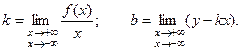
Практически целесообразно искать асимптоты в следующем порядке: 1) вертикальные асимптоты (если есть точки разрыва 2 – го рода 2) наклонные асимптоты. Горизонтальная асимптота - частный случай наклонной асимптоты при 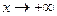 или
или 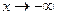 . Горизонтальная асимптота - это частный случай наклонной асимптоты при
. Горизонтальная асимптота - это частный случай наклонной асимптоты при 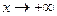 или
или 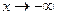 , в случае, если
, в случае, если 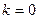 .
.
ЗАМЕЧАНИЕ 1. Если хотя бы одно из чисел либо 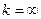 , либо
, либо 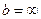 , то график функции не имеет ни наклонной ни горизонтальной асимптоты.
, то график функции не имеет ни наклонной ни горизонтальной асимптоты.
ЗАМЕЧАНИЕ 2. график функции не может иметь больше двух наклонных асимптот.
ПРИМЕР. Найти асимптоты графика функции
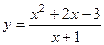 и построить её график.
и построить её график.
В область определения этой функции не входит точка 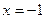 . Найдём в этой точке односторонние пределы.
. Найдём в этой точке односторонние пределы.
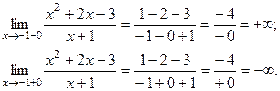
Следовательно, 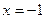 - вертикальная асимптота графика.
- вертикальная асимптота графика.
Найдём наклонную асимптоту: 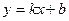 .
. 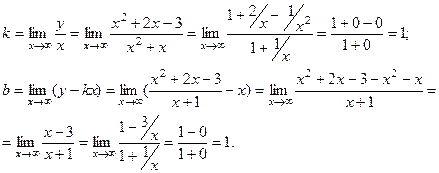 Таким образом, наклонная асимптота имеет уравнение
Таким образом, наклонная асимптота имеет уравнение 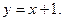
Чтобы поточнее построить график, найдём ещё нули функции: если 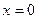 , то
, то 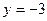 ; если
; если 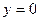 , то
, то 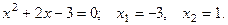
Пунктирными линиями на графике построим асимптоты.

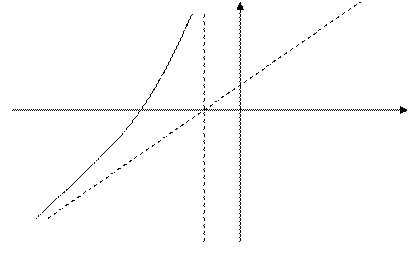 У
У
-3 -1 О 1 х
-3
7.3. Схема полного исследования функции
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат (нули функции).
3. Исследовать функцию на «чётность - нечётность». Если 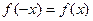 , то функция называется чётной и её график симметричен относительно оси Оу. Если
, то функция называется чётной и её график симметричен относительно оси Оу. Если 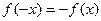 , то функция называется нечётной и её график симметричен относительно начала координат. Если функция не является ни чётной ни нечётной, то её называют функцией общего вида.
, то функция называется нечётной и её график симметричен относительно начала координат. Если функция не является ни чётной ни нечётной, то её называют функцией общего вида.
4. Проверка периодичности функции (обычно для тригонометрических функций).
5. Найти асимптоты (вертикальные, наклонные)
6. Исследование с помощью 1-й производной (критические точки, интервалы монотонности, экстремумы).
7. Исследование с помощью 2-й производной (интервалы выпуклости, точки перегиба).
8. Построение графика.
Рассмотрим примеры.
1 Провести полное исследование и построить график функции 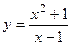 .
.
1) Область определения: 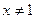 , т.е.
, т.е.
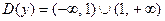 .
.
2). Нули функции: 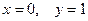 .
. 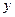 в ноль обращаться не может.
в ноль обращаться не может.
3). 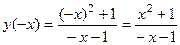 .
. 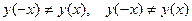
следовательно функция общего вида.
4). Не периодична.
5). Асимптоты. Вертикальная асимптота возможна в точке 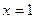 . Найдём в этой точке односторонние пределы.
. Найдём в этой точке односторонние пределы.
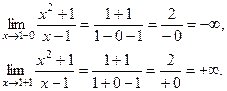
Следовательно, 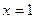 - вертикальная асимптота.
- вертикальная асимптота.
Найдём наклонную асимптоту.
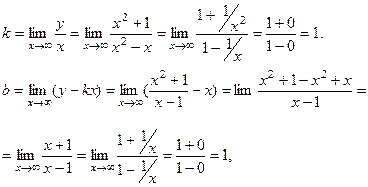
т.е. наклонная асимптота имеет уравнение 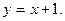
6). Исследование с помощью 1-й производной.
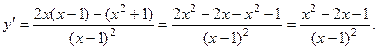
Критические точки: 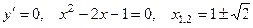 .
.
Определим интервалы монотонности и точки экстремума. Пост- роим числовую ось
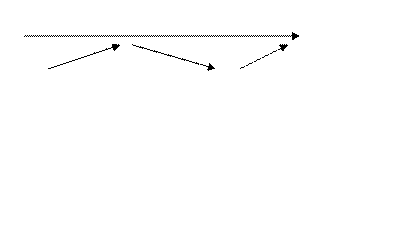
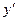 +
+ 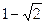 -
- 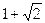 +
+
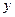 1
1
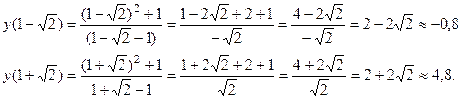
6. Исследование с помощью 2-й производной
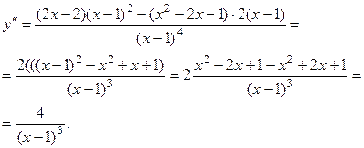
Построим числовую прямую


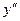 - 1 + х
- 1 + х

Построим график


Y
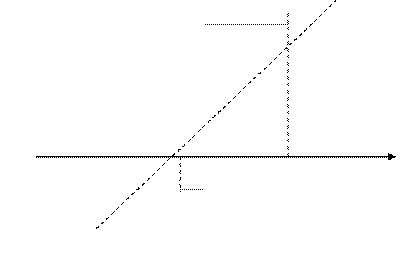
 4,8
4,8
-1 -0,4 O 1 2,4 x
 - 0,8
- 0,8
2. Провести полное исследование и построить график функции 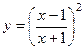 .
.
1). Область определения этой функции: 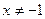 , или
, или 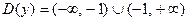 .
.
2). Нули функции: 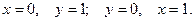
3). 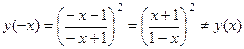 и
и 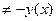 , т.е. функция общего вида.
, т.е. функция общего вида.
4). Не периодична.
5). Вертикальная асимптота возможна в точке 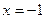 . Найдём односторонние пределы в этой точке:
. Найдём односторонние пределы в этой точке:
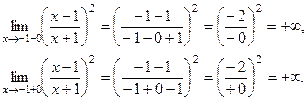
В точке 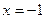 график имеет вертикальную асимптоту.
график имеет вертикальную асимптоту.
Найдём наклонную асимптоту в виде 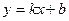 .
.
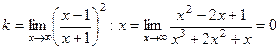 , так как степень числителя меньше степени знаменателя.
, так как степень числителя меньше степени знаменателя.
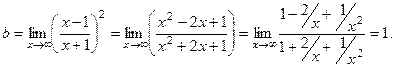
Таким образом, график имеет горизонтальную асимптоту 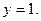
6). Исследование с помощью 1-й производной:
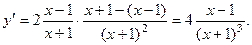
Критическая точка : 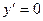 при
при 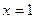 . Построим числовую прямую
. Построим числовую прямую
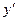 + -1 - 1 + х
+ -1 - 1 + х
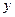
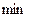
7) Исследование с помощью 2-й производной:
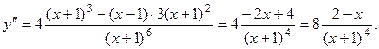
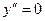 при
при 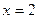 . Построим числовую ось:
. Построим числовую ось:
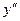 + -1 + 2 _ х
+ -1 + 2 _ х
8). Осталось построить график
 |  | ||
у
-1 О
1 2 х
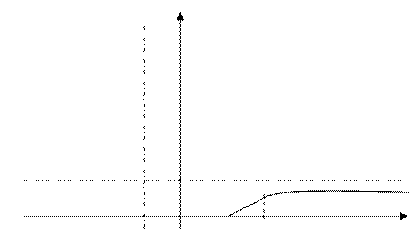
Рассмотрим ещё один пример для случая, когда график функции имеет одностороннюю асимптоту
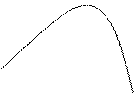
3. Провести полное исследование и построить график функции 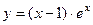 .
.
1). Область определения этой функции - вся числовая прямая.
2) Нули функции: 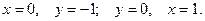
3). 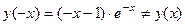 и
и 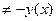 , т.е. функция общего вида.
, т.е. функция общего вида.
4).. Не периодичная.
5). Вертикальных асимптот нет, так как нет точек разрыва.
При нахождении наклонных асимптот придётся отдельно находить пределы при 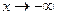 и
и 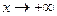 , из - за свойств показательной функции.
, из - за свойств показательной функции.
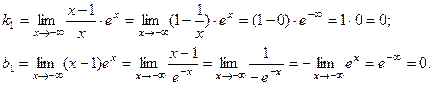 (При вычислении второго предела мы использовали правило Лопиталя). Итак, при
(При вычислении второго предела мы использовали правило Лопиталя). Итак, при 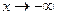 график имеет горизонтальную асимптоту
график имеет горизонтальную асимптоту 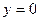 .
. 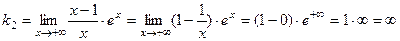
Следовательно, при 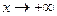 график асимптоты не имеет.
график асимптоты не имеет.
6). 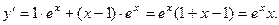
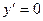 при
при 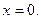 Если
Если 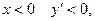 при
при 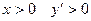 .
.
Следовательно, в точке 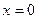 функция имеет минимум
функция имеет минимум 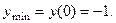
7). Найдём вторую производную
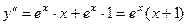 .
.
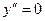 при
при 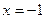 . Если
. Если 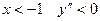 и график имеет выпуклость, направленную вверх. Если
и график имеет выпуклость, направленную вверх. Если 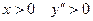 и график имеет выпуклость, направленную вниз.
и график имеет выпуклость, направленную вниз.
Построим график функции.
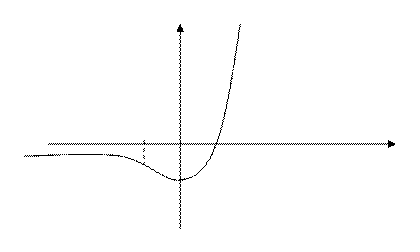
Y
-1 0 1 x
-1
Таким образом можно построить график любой функции.
Библиографический список.
