Решение систем обыкновенных дифференциальных уравнений

Для решения систем обыкновенных дифференциальных уравнений в сис­теме MATLAB имеются функции: ode23, ode45, odell3, odel5s, ode23s, ode23t и ode23tb.

Функции с суффиксом s предназначены для решения так называемых сис­тем жестких дифференциальных уравнений, а для всех остальных систем дифференциальных уравнений наиболее употребительной является функция

ode45, реализующая алгоритм Рунге- Кутта 4-5-го порядка (разные порядки точности используются для контроля шага интегрирования).

Пусть необходимо решить систему n дифференциальных уравнений, раз­решенных относительно первых производных функций у1, у2, ..., уn (это все функции от х):

у1' = Fl( х, у1, у2, ..., уn );

у2' = F2( х, у1, у2, ..., уn );

...уn' = Fn( х, у1, у2, ..., уn).

Введем вектор-столбцы Y и F, состоящие из у1, у2, ..., уn и Fl, F2, ..., Fn, соответственно. Тогда система дифференциальных уравнений примет следую­щий векторный вид:

Y' = F( х, Y ).

Чтобы применить «решатель» ode45, нужно оформить в виде функции пользо­вателя правую часть системы уравнений F( х, Y ).

Пусть, к примеру, требуется решить дифференциальное уравнение:

y′′ + y + K⋅x²=0 с начальными условиями:

y(0) = 1

y′(0)=0 .

Данное дифференциальное уравнение второго порядка приведем к системе дифференциальных уравнений первого порядка:

у1' = у2 + К * х * х;

у2' = -у1.

с начальными условиями у 1(0) = 0, у2(0) = 1. Здесь К- коэффициент нели­нейности задачи. При К = 0 задача становится чисто линейной и описывает гармонические колебания. Если постепенно увеличивать значение коэффициен­та К и находить соответствующие решения, то можно будет наглядно наблю­дать постепенное проявление нелинейного характера колебаний.

Для данного примера неизвестная вектор-функция Y состоит из двух эле­ментов:

Y = [ у1, у2 ].

Так как функции у1 и у2 вычисляются во многих точках в процессе нахождения решения, то реально у1 и у2 являются вектор-столбцами. Вектор F правых час­тей системы уравнений для, К = 0.01, вычисляем с помощью собственной функции MyDifEql:

function F = MyDifEql( х, у) F = [ 0.01 * х * х + y(2); -y(l) ];

текст которой записываем в файл MyDifEql.m. Эта функция вызывается каждый раз, когда требуется вычислить правые части уравнений в конкретной точке х, так что здесь х является скаляром, а вектор у состоит всего из двух элементов. Теперь можно вызывать функцию ode45,находящую решение нашей системы дифференциальных уравнений с начальными условиями [0,1] на отрезке [0,20].

[ X, Y ] = ode45( 'MyDifEql',[0,20],[0,1] );

Решения уравнений с помощью команды: plot (X, Y(:, 1), X, Y(:, 2))

отображаются на графике (Y(:, 1) – первый столбец матрицы решений, Y(:, 2) – второй ее столбец).

Теперь перейдем к так называемым жестким системам дифференциаль­ных уравнений, решения которых на разных отрезках изменения независимых переменных ведут себя абсолютно по-разному: в одних местах наблюдается чрезвычайно быстрое изменение зависимых переменных, в то время как в дру­гих местах имеет место их сверхмедленная эволюция. Это слишком сложный характер поведения для обычных алгоритмов численного решения дифферен­циальных уравнений. Поэтому для надежного решения жестких систем уравне­ний применяют специальные методы. Решим дифференциальное уравнение Ван-дер-Поля, которое описывает нелинейные релаксационные колебания в раз­личных электронных устройствах:

у1' = у2; у2' = -y1 + К * (1 - у1 * у1) * у2

с начальными условиями у1(0) =2, у2(0) = 0.

Здесь К = 1000 - большой коэффи­циент нелинейности задачи.

Составим функцию MyVanDerPol, которая описы­вает правые части представленных дифференциальных уравнений:

function F = MyVanDerPol( х, у ) F = [ у(2); -у(1) + 1000*( 1 - у(1)^2 ) * у(2) ].

Для решения дифференциальных уравнений Ван-дер-Поля на отрезке из­менения независимой переменной [0, 3000] используем «решатель» odel5s: [X, Y] = odel5s ( 'MyVanDerPol', [0,3000], [2,0] ), после чего визуализируем решение.

Символьные вычисления. Возможности встроенного пакета символьных вычислений и операций Symbolic Math Toolbox достаточно обширны, рассмотрим лишь некоторые его возможности.

Под символьным объектом в системе MATLAB понимается переменная, предназначенная для символьных преобразований. Объявление такой перемен­ной осуществляется функцией sym либо syms. Функция sym используется при объявлении какой-либо одной переменной символьной, например: sym x – объявление символьной переменной х.

Упростим выражение: (используется функция simplify)

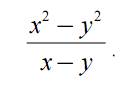
» sym x;

» sym y;

» simplify((x^2-y^2)/(x-y))

ans = х+у

Функция syms позволяет объявлять сразу несколько символьных перемен­ных, которые необходимо отделять друг от друга пробелами, например:

42 » syms x y z;

Упрощение тригонометрических, логарифмических, экспоненциальных функций и полиномов осуществляется функцией expand, формат обращения к которой имеет следующий вид:

rez=expand(S) ,

где S - символьное выражение, которое нужно упростить;

rez - результат упрощения. Например:

» syms x y;

» rezl=expand(sin(x+y)

rezl = sin (x) *cos (у) +cos (x) *sin (y)

Для выполнения операции дифференцирования используется функция diff, формат обращения к которой имеет следующий вид: diff(y(x)),

где у(х) - явно заданная функция. Ниже приведен пример, иллюстрирующий работу этой функции:

» syms x;

» D=diff (x^2+4*x^5)

D = 2*x+20*x^4

Для того чтобы продифференцировать заданную функцию n раз, нужно обратиться к ней следующим образом: D =diff (S, 'v' ,n), где S - дифференцируемое выражение, v - переменная дифференцирования.

Следующий пример иллюстрирует дифференцирование заданного выра­жения S дважды по переменной х.

» syms x у;

» S=x^3*y^2+sin(x*y) ;

» D=diff (S,'x' ,2)

D = 6*x*y^2-sin (x*y)*y^2

Для решения дифференциальных уравнений в MATLAB зарезервирована функция dsolve, которая имеет следующие форматы обращения:

1. y=dsolve( 'Dy(x)' ) ,

где Dу(х) -уравнение; у - возвращаемые функцией dsolve решения.

2. y=dsolve ('Dy (x)' , ' НУ ' ) ,

где Dу(х) -уравнение; НУ - начальные условия. Первая производная функции обозначается Dу, вторая производная – D2у и так далее.

Функция dsolve предназначена также для решения системы дифференци­альных уравнений. В этом случае она имеет следующий формат обращения: [f,g]=dsolve('Df(x),Dg(x)', 'НУ'), где Df(x) ,Dg(x) - система уравнений; НУ - начальные условия.

Например: решить дифференциальное уравнение:

у'(х) = 0.6-0.2y(x) c начальным условием у(0)=0.

» dsolve(' Dy = 0.6 - 0.2*y ', ' у(0)=0 ')

ans = 3+exp(-l/5*t)*3.

Перечислим еще несколько функций, часто используемых при символьных вычислениях:

expand – раскрывает алгебраические и функциональные выражения;

factor – раскладывает многочлены на простейшие множители;

det – вычисляет определитель символьной матрицы;

inv – вычисляет обратную матрицу;

int – вычисляет неопределенный интеграл;

limit –вычисляет пределы;

taylor – осуществляет разложение функций в ряд Тейлора;

solve – решает алгебраическое уравнение и систему алгебраических урав­нений.

Порядок выполнения лабораторной работы 2. Задание 1.Решить систему уравнений:

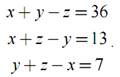
Задание 2.Определить абсциссы точек пересечения графиков функций:

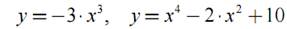
Задание 3.Вычислить предел:

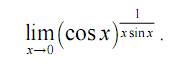
Задание 4.Найти производную от функции y(x):

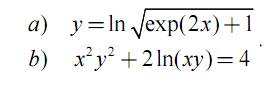
Задание 5.Найти вторую производную от функции:

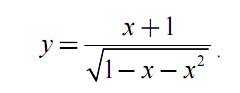
Задание 6.Вычислить определенный интеграл:

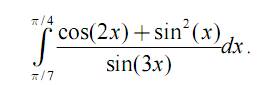
Задание 7.Вычислить двойной интеграл:

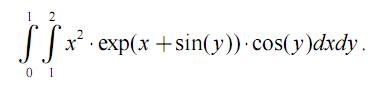
Задание 8. Вычислить неопределенный интеграл:

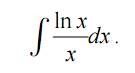
Задание 9. Решить дифференциальное уравнение и построить график

функции y(x) на отрезке [1,10]:

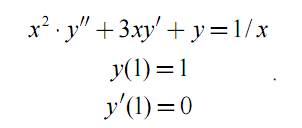
Задание 10. Решить дифференциальное уравнение:

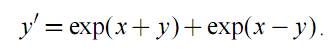
Контрольные вопросы

1. Что называют операцией правого и левого деления матриц?

2. Как задать функцию пользователя в системе MATLAB?

3. Как можно приближенно определить нули функции?

4. Как можно достигнуть большей точности при нахождении нулей функции?

5. Как определяются корни многочлена в системе MATLAB?

6. Как вычислить определенный интеграл и двойной интеграл в системе MATLAB?

7. Опишите схему нахождения решений системы дифференциальных уравне­ний с начальными условиями?

8. Как произвести упрощение алгебраического выражения в системе MAT­LAB?

9. Как символьно определить производную n-ого порядка от явно и неявно за­данных функций?

10. Опишите функцию dsolve.

Приложение 1 Стандартные функции вещественного аргумента

Экспоненциальные функции

a^x	Степенная функция
x^a	Показательная функция
sqrt(x)	Квадратный корень
exp(x)	Экспонента
log(x)	Натуральный логарифм
log10(x)	Десятичный логарифм
abs(x)	Модуль
fix(x)	Отбрасывание дробной части числа
floor(x)	Округлениие до меньшего целого
ceil(x)	Округлениие до большего целого
round(x)	Обычное округление
rem(x,y)	Остаток от деленияx x на y без учёта знака
mod(x,y)	Остаток от деленияx x на y с учёта знака
sign(x)	Знак числа
factor(x)	Разложение числа x на простые множители

Тригонометрические функции

sin(x)	Синус
sinh(x)	Синус гиперболический
asin(x)	Арксинус
asinh(x)	Арксинус гиперболический
cos(x)	Косинус
cosh(x)	Косинус гиперболический
acos(x)	Арккосинус
acosh(x)	Арккосинус гиперболический
tan(x)	Тангенс
tanh(x)	Тангенс гиперболический
atan(x)	Арктангенс

atanh(x)0	Арктангенс гиперболический
cot(x)	Котангенс
coth(x)	Котангенс гиперболический
acot(x)	Арккотангенс
acoth(x)	Арккотангенс гиперболический

Приложение 2 Системные переменные MATLAB

i, j	Мнимая единица
pi	Число π
eps	Погрешность для операций над числами с плавающей точкой (по умолчанию 2-52)
realmin	Минимальное значение вещественного числа
realmax	Максимальное значение вещественного числа
inf	Бесконечность
NaN	Неопределённость
ans	Переменная, хранящая результат последней операции

Приложение 3 Функции комплексных переменных

abs	Абсолютное значение комплексного числа
conj	Комплексно-сопряжённое число
imag	Мнимая часть комплексного числа
real	Действительная часть комплексного числа
angle	Аргумент комплексного числа
isreal	“Истина”, если число действительное