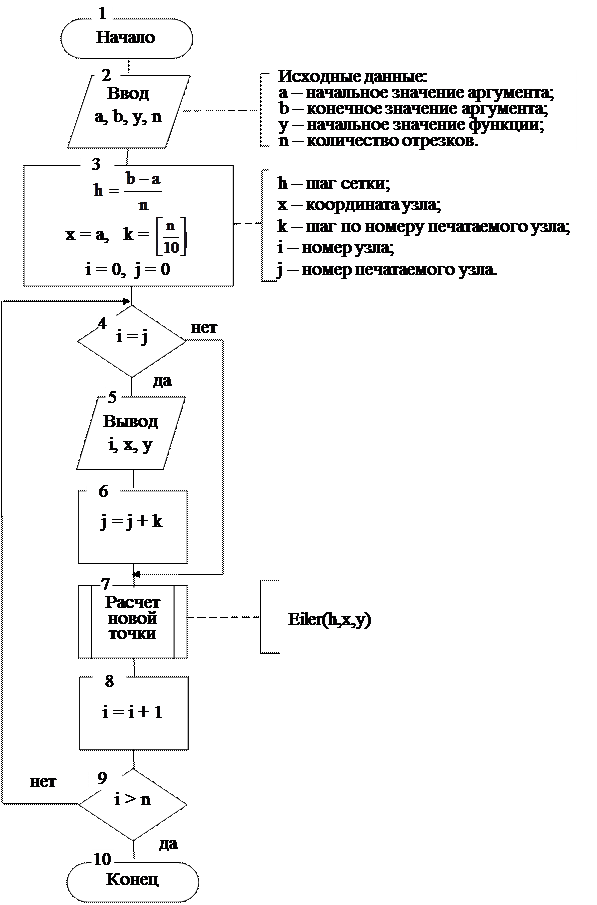
Решение обыкновенных дифференциальных уравнений.

Уравнение, содержащее производные от искомой функции y = y(x), называется обыкновенным дифференциальным уравнением (ОДУ).

Общий вид дифференциального уравнения:

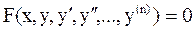(7.1)

где n – наивысший порядок производной, определяет порядок уравнения.

Решением ОДУ называется функция y = y(x), которая после ее подстановки в уравнение (7.1) обращает его в тождество.

Общее решение ОДУ имеет вид:

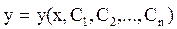(7.2)

где C₁, C₂, …, C_n – постоянные интегрирования.

Задача Коши. Все условия заданы в одной, начальной точке, поэтому они называются начальными условиями.

Примеры постановки задачи Коши:

Краевая задача. Условия заданы в более чем одной точке, обычно в начальной и конечной. Условия в этом случае называются краевыми или граничными. Такая задача может возникнуть только при решении ОДУ с порядком выше первого.

Примеры краевых задач:

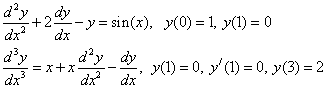
Численные методы решения задачи Коши для ОДУ:

Постановка задачи. Найти решение ОДУ первого порядка

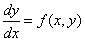на отрезке 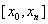при условии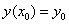

При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом 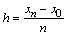, расчетными узлами служат точки 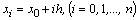промежутка [x₀, x_n].

Целью является построение таблицы

xi	x0	x1	…	xn
yi	y0	y1	…	yn

т.е. ищутся приближенные значения y в узлах сетки.

Интегрируя уравнение на отрезке 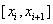, получим

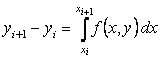
Воспользовавшись простейшей формулой левых прямоугольников первого порядка

,

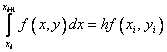получаем явную формулу Эйлера:

, .

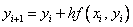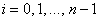Порядок расчетов:

Зная 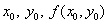, находим 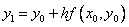, затем 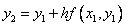т.д.

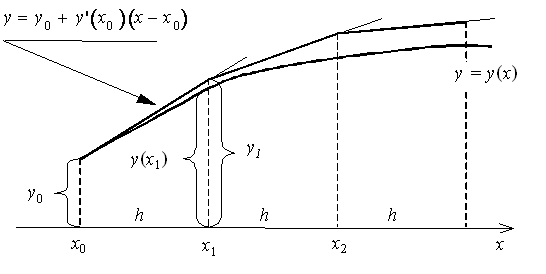
Геометрическая интерпретация метода Эйлера:

Пользуясь тем, что в точке x₀ известно решение y(x₀) = y₀ и значение его производной 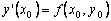, можно записать уравнение касательной к графику искомой функции 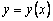в точке 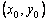: 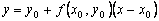. При достаточно малом шаге h ордината 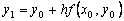этой касательной, полученная подстановкой в правую часть значения 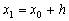, должна мало отличаться от ординаты y(x₁) решения y(x) задачи Коши. Следовательно, точка 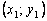пересечения касательной с прямой x = x₁ может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую 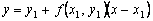, которая приближенно отражает поведение касательной к 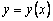в точке 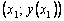. Подставляя сюда 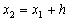(т.е. пересечение с прямой x = x₂), получим приближенное значение y(x) в точке x₂: 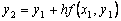и т.д. В итоге для i–й точки получим формулу Эйлера.

Явный метод Эйлера имеет первый порядок точности или аппроксимации.

Если использовать формулу правых прямоугольников: 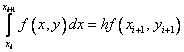, то придем к методу

, .

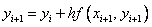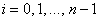Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения 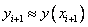по известному значению 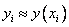требуется решать уравнение, в общем случае нелинейное.

Неявный метод Эйлера имеет первый порядок точности или аппроксимации.

Модифицированный метод Эйлера: в данном методе вычисление 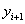состоит из двух этапов:

Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.

Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(x_i+1) по формуле вида

,

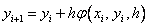где

…………………………………………….

.

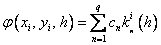
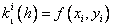
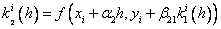
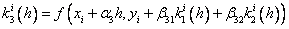
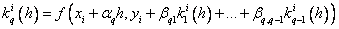Здесь a_n, b_nj, p_n, 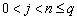– некоторые фиксированные числа (параметры).

При построения методов Рунге–Кутты параметры функции 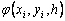(a_n, b_nj, p_n) подбирают таким образом, чтобы получить нужный порядок аппроксимации.

Схема Рунге – Кутта четвертого порядка точности:

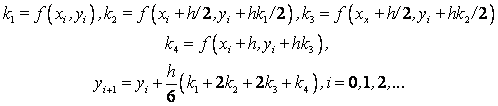
24.)

Метод Эйлера (метод Рунге-Кутта 1-го порядка).

Разобьем [a, b] на n равных частей – элементарных отрезков, x₀, x₁,…,x_n будем называть узлами сетки, h = (b-a)/n - шаг сетки.

, ; , .

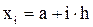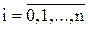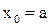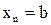Заменим в уравнении 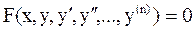y^’ в точке x_i её приближенной оценкой – отношением приращений (это следует из определения производной):

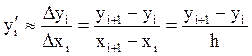
Тогда получаем:

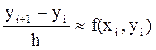
Отсюда формула Эйлера:

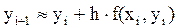
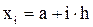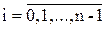, – номер узла

Зная y₀ в точке x₀ (начальное условие) можно найти y₁, затем, используя уже известные значения x₁ и y₁, вычислить x₂ и y₂ и так далее.

Рассмотрим геометрическую иллюстрацию метода Эйлера. В координатах (x,y) отобразим известные данные: отрезок [a,b] на оси Х и начальное условие y₀ – точка А с координатами (a, y₀). Отрезок [a,b] разобьем на n равных частей, получим узлы равномерной сетки a = x₀, x₁, x₂, … , x_n = b. Вычислим значения первой производной искомой функции в точке А, используя координату этой точки и исходное уравнение y^’ = f(x,y)

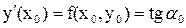
Полученное значение позволяет построить касательную к искомой функции в точке А. Эту касательную можно использовать для вычисления приближенного значения искомой функции в новом узле х₁ (кривую y(x) заменяем на отрезком АВ на элементарном отрезке [x₀, x₁]).

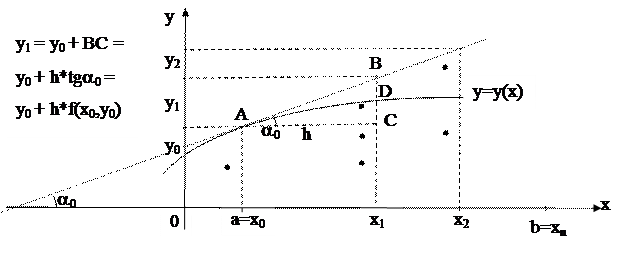Геометрическая иллюстрация метода Эйлера.

Зная (x₁,y₁), можно аналогично получить новую точку (x₂,y₂) и т.д.

Алгоритм расчета новой точки методом Эйлера: