Конъюнктивные нормальные формы

Определение. Элементарной дизъюнкцией называется дизъюнкция литералов (переменных или их отрицаний), взятых не более чем по одному разу.

Например, дизъюнкции 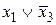, , 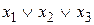1 являются элементарными. Причем первая элементарная дизъюнкция имеет ранг (число литералов) 2, вторая - 3, а третья - 0.

Следующие дизъюнкции: 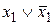, , 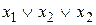, , 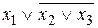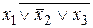0 не являются элементарными.

Определение.Элементарная дизъюнкция булевой функции 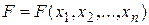, содержащая n литералов, называется полной.

Определение. Конъюнкция любого конечного множества элементарных дизъюнкций булевой функции F называется конъюнктивной нормальной формой (КНФ) функции F. Число элементарных дизъюнкций, составляющих КНФ, называется длиной КНФ.

Например, КНФ 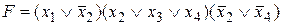имеет длину, равную 3.

Для произвольной булевой функции F существует, вообще говоря, много различных реализующих ее КНФ, отличающихся друг от друга длиной, числом вхождений литералов и т.д.

Определение. Две (или несколько) КНФ, реализующих одну и ту же булеву функцию F , называются эквивалентными (или равносильными).

Определение. КНФ булевой функции F, состоящая только из полных элементарных дизъюнкций, называется совершеннойКНФ(СКНФ).

Например, 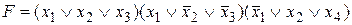- СКНФ функции F, заданной вектором значений таблицы истинности w(F)=(01100111).

Отметим, что КДНФ является единственной (с точностью перестановки множителей) для конкретной булевой функции F .

Любую булеву функцию F, заданную формулой, можно с помощью основных равносильностей преобразовать к КНФ, а затем к СКНФ.

Пример.Привести к виду СКНФ булеву функцию F= .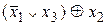

Решение.С помощью основных равносильностей преобразуем к КНФ:

= = = =

=

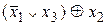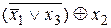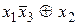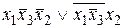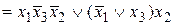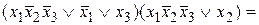
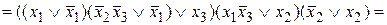
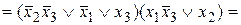
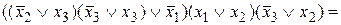
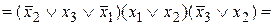
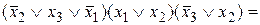
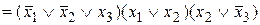― КНФ.

В данном примере сначала выразили функцию только с помощью операций дизъюнкции, конъюнкции и отрицания, а затем несколько раз применили формулу 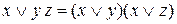, группируя переменные таким образом, чтобы каждый раз одна скобка в конъюнкции сокращалась по формуле .

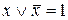Применяя закон склеивания (в обратном порядке: 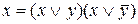), дополняем дизъюнкции 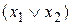, 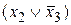до полных элементарных дизъюнкций:

.

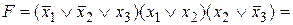
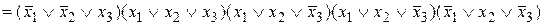Так как 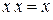, то после сокращения одинаковых конъюнкций получаем СКНФ: F .

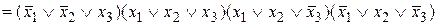Составим таблицу истинности для булевой функции F= 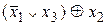(функция из предыдущего примера). Отметим связь между СКНФ и таблицей истинности.

Таблица истинности СКНФ

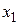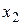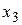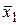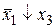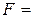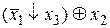						Элементарные дизъюнкции СКНФ

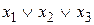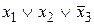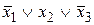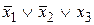В общем случае также можно вывести закономерности построения СКНФ по таблице истинности булевой функции, что является очень удобным.

СКНФ состоит из конъюнкций полных элементарных дизъюнкций наборов переменных 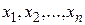, на которых функция принимает значение 0. Переменные берутся без отрицания, если им соответствует в таблице истинности 0, с отрицанием, если 1.

Пример. По таблице истинности составить СКНФ.

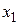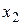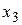			F

Решение: F .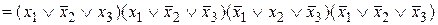

Пример. Для булевой функции, заданной в виде ДНФ 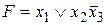, составить КНФ, СКНФ и выполнить проверку по таблице истинности.

Решение: Применяя формулу 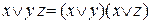, из ДНФ получаем КНФ:

.

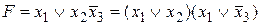Применяя закон склеивания (в обратном порядке: 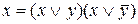), дополняем дизъюнкции 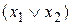, 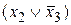до полных элементарных дизъюнкций:

.

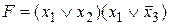
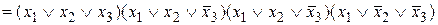Так как 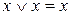, то после сокращения одинаковых дизъюнкций получаем СКНФ:

.

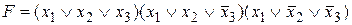Таблица истинности СКНФ

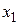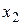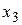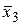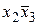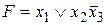						Элементарные дизъюнкции СКНФ

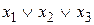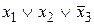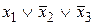Основы теории графов

Графические представления в широком смысле – любые наглядные отображения исследуемой системы, процесса, явления на плоскости. К ним могут быть отнесены рисунки, чертежи, графики зависимостей характеристик, планы-карты местностей, блок-схемы процессов, диаграммы и т.п. такие изображения наглядно представляют различные взаимосвязи, взаимообусловленности: топологическое (пространственное) расположение объектов, хронологические (временные) зависимости процессов и явлений, логические, структурные, причинно-следственные (каузальные) и другие взаимосвязи.