Решение обыкновенных дифференциальных уравнений и систем

Некоторые задачи вычислительной математики

Решение задач линейной алгебры.

Пусть A – квадратная матрица.

Для вычисления определителя предназначена встроенная функция det:

D = det(A)

Для нахождения обратной матрицы служит встроенная функция inv:

A1 = inv(A)

Для того чтобы задать в MATLAB систему линейных уравнений 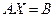необходимо ввести основную матрицу системы 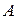и вектор правой части 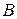, например, для системы

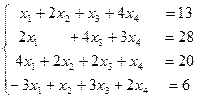
основная матрица системы:

>> A = [1 2 1 4; 2 0 4 3; 4 2 2 1; -3 1 3 2]

вектор правой части:

>> B = [13; 28; 20; 6]

Решение системы линейных алгебраических уравнений 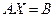в MATLAB можно выполнить при помощи символа \ .

Решение системы:

>> X = A\B

X =

-1

Проверка

>> A *X

В результате должны получить вектор B.

ans =

13.0000

28.0000

20.0000

6.0000

Интегрирование функций

Вычисление определенных интегралов

В MatLab существует встроенная функция, реализующая алгоритм метода Симпсона с автоматическим выбором шага

I = quad('имя функции', а, b)

где

имя функции – имя функции, задающей подынтегральное выражение;

а, b – пределы интегрирования,

I – значение интеграла.

Для повышения точности вычислений следует задать дополнительный четвертый аргумент e – точность метода:

I = quad('name', а, b, e).

Например, требуется вычислить определенный интеграл

.

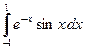Подынтегральную функцию можно вводить разными способами:

Первый способ.

Создаем файл-функцию, для вычисления подынтегрального выражения и сохраняем её, например, под именем fint

------------------------------------------------------------------------------------------------------------------------

function f = fint(x)

f = exp(­-x).*sin(x);

------------------------------------------------------------------------------------------------------------------------

Затем, например, в командном окне выполним команду

>> I = quad('fint', -1, 1)

Выведем результат в формате long

I =

-0.66349146785310

Для повышения точности вычислений следует задать дополнительный четвертый аргумент:

>> I = quad('fint', -1, 1, 1.0e-10)

I =

-0.66349366663001

Второй способ.

Подынтегральную функцию можно вводить и как строку, используя команду inline:

>> F = inline('exp(-x).* sin(x)')

F =

Inline function:

F(x) = exp(-x).* sin(x)

Далее вызываем встроенную функцию quadс тремя входными аргументами, при этом имя функции пишется без апострофов:

>> I = quad(F, -1, 1)

I =

-0.66349146785310

Третий способ.

Подынтегральную функцию можно вводить, используя символ @:

>> F = @(x)exp(-x).*sin(x)

F =

@(x)exp(-x).*sin(x)

>> I = quad(F, -1, 1)

I =

-0.6635

Вычисление интегралов, зависящих от параметра.

Пусть требуется вычислить интеграл

,

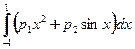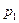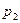где x – независимая переменная, и – параметры. Вычислим этот интеграл при значениях параметров

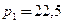и .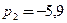

Первый способ.

Создаем файл-функцию, зависящую от трех входных аргументов:

------------------------------------------------------------------------------------------------------------------------

function f = fparam(x, par1, par2)

f = par1.*x.^2+par2.*sin(x);

------------------------------------------------------------------------------------------------------------------------

Для вычисления интеграла используем quad, в командном окне

I = quad('fparam', -1, 1, 1.0e-06 , 0, 22.5, -5.9)

I =

При вычислении интеграла, зависящего от параметров, их следует указывать, начиная с шестого аргумента quad.

( Цифра ''0'' на месте пятого аргумента подавляет вывод узлов интегрирования на экран)

Второй способ.

Подынтегральную функцию вводим как строку

>> F = inline('par1.*x.^2+par2.* sin(x)','x','par1','par2')

F =

Inline function:

F(x,par1,par2) = par1.*x.^2+par2.* sin(x)

Затем снова используем quad в виде

>> I = quad(F, -1, 1,1.0e-10 , 0,22.5,-5.9)

I =

15.0000

Третий способ.

>> f = @(x, par1, par2) par1.*x.^2+par2.* sin(x)

f =

@(x,par1,par2)par1.*x.^2+par2.*sin(x)

>> I = quad(f, -1, 1,1.0e-10 , 0,22.5,-5.9)

I =

15.0000

Вычисление интегралов от функций, заданных в виде таблицы.

Пусть функция 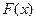задана таблицей своих значений в точках 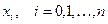, ( 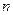– четное) с постоянным шагом :

		………………..
		………………..

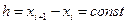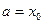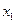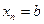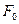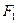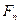Формула Симпсона для численного интегрирования имеет вид

.

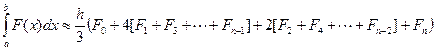Напишем М-функцию f_simps, реализующую алгоритм метода Симпсона в MatLab

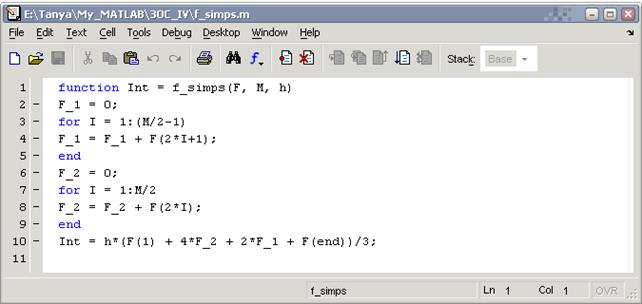
Здесь: F – вектор значений табличной функции, M – четное число интервалов на которые разделён отрезок 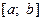, h – шаг таблицы.

Например, для функции 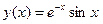создадим таблицу, разделяя отрезок 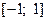на 10 интервалов и для полученной табличной функции вычислим приближенное значение интеграла 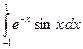, используя функцию f_simps.

Выполняем в команды:

M = 10;

a = -1;

b = 1;

h = (b-a)/M;

x = a:h:b;

F = exp(-x).*sin(x);

Int = f_simps(F, M, h)

Int =

-0.6635

Приближение функций

1. Многочлены.

Многочлен в MatLab задается вектором его коэффициентов. Например, введем многочлен

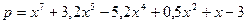
p = [1 0 3.2 -5 .2 0 0.5 1 -3]

Значение многочлена в точке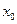

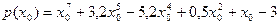
вычисляет команда polyval, например, в точке :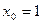

polyval(p, 1)

Аргумент может быть матрицей или вектором, при этом результат также будет матрицей или вектором.

2. Интерполяционный многочлен.

Пусть задана сеточная функция

x			…..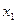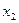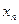
y			…...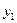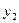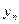

и требуется приблизить эту сеточную функцию многочленом

,

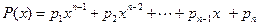удовлетворяющим условиям интерполяции:

.

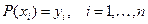Коэффициенты интерполяционного многочлена 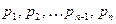– решение системы линейных уравнений

.

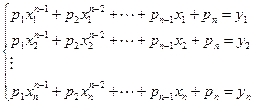Матрица этой системы представляет собой, так называемую матрицу Вандермонда, которая в MatLabзадается функцией vander.Неизвестные коэффициенты 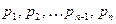можно найти путем левого матричного деления «\».

Например, построим интерполяционный многочлен для заданной таблицы

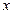	0,5
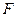	1,5				1,2

и вычислим приближенное значение 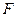при .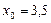

Создадим М-файл list_12.

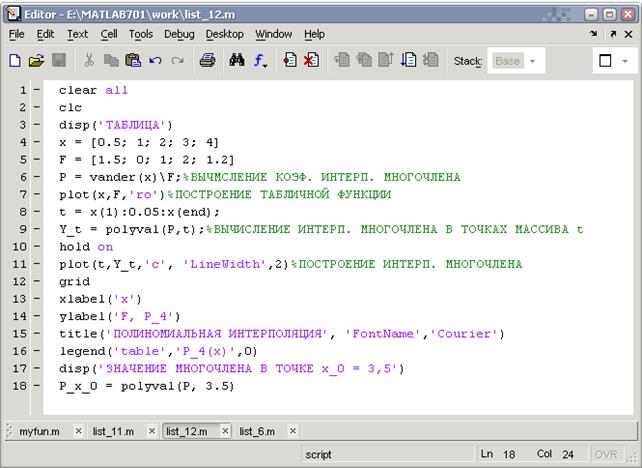
В результате работы программы получим графики табличной функции и интерполяционного многочлена:

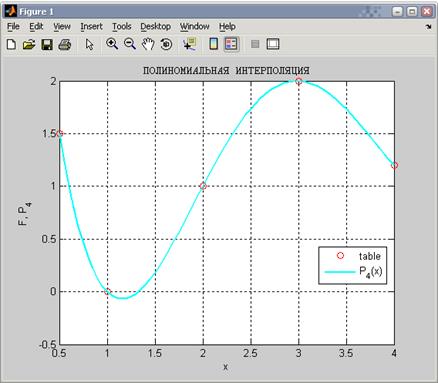
и вывод в командном окне

ТАБЛИЦА

0.5 1 2 3 4

1.5 0 1 2 1.2

ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН P_4

0.21905 -2.4905 9.4667 -13.252 6.0571

ЗНАЧЕНИЕ МНОГОЧЛЕНА В ТОЧКЕ x_0 = 3.5

P_x_0 =

1.7321

3. Кусочно-многочленная интерполяция.

1) Интерполяция по соседним элементам

– способ интерполяции данных, при которой значения в каждой промежуточной точке принимается равным ближайшему значению, заданному в таблице.

2) Линейная интерполяция

– это способ, при котором соседние точки соединены отрезками прямых.

3) Интерполяция сплайнами.

Все эти способы интерполяции реализуются встроенной функцией interp1.

yi = interp1(x, y, xi, ’method’)

x – массив абсцисс табличной функции;

y – массив ординат табличной функции;

xi – промежуточные точки, в которых необходимо вычислить значения интерполирующей функции;

Параметр method может принимать одно из следующих значений:

nearest – интерполяция по соседним элементам;

liner– линейная интерполяция;

spline– интерполяция кубическим сплайном.

Выходным аргументом interp1 является вектор yi значений интерполирующей функции.

Рассмотрим таблицу из предыдущего примера и построим для неё различные интерполирующие функции. Текст программы приведем в list_13.

Графики

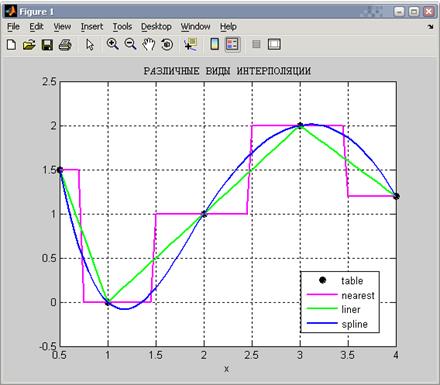
Вывод в командное окно

ТАБЛИЦА

0.5 1 2 3 4

1.5 0 1 2 1.2

ЗНАЧЕНИЕ ИНТЕРП. ФУНКЦИЙ В ТОЧКЕ x_0 = 3,5

Near_x_0 =

1.2

Line_x_0 =

1.6

Spline_x_0 =

1.8618

ynear_X1 = 1

4. Метод наименьших квадратов.

Пусть некоторая функция 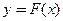задана своими табличными значениями 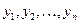в п различных точках ( ).

		………………..
		………………..

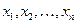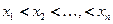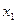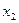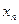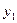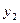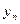Требуется найти многочлен степени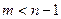

,

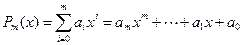коэффициенты которого 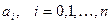минимизируют функцию

.

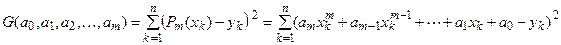Построение полинома, который приближает функцию, заданную таблицей, по методу наименьших квадратов в MatLab осуществляется при помощи polyfit:

pk = polyfit(x, y, k),

x – массив абсцисс экспериментальных точек;

y – массив ординат экспериментальных точек;

k – степень аппроксимирующего полинома.

Результатом работы функции является массив pk коэффициентов полинома. Для того чтобы вычислить значение аппроксимирующего полинома в любой точке применяют функцию

Pk = polyval(pk, t),

где t – точка (или массив точек) в которой необходимо вычислить значение многочлена.

Например, для заданной таблицы

x
y	0.5	0.5

построим многочлен третьей степени по методу наименьших квадратов. Текст программы в list_14.

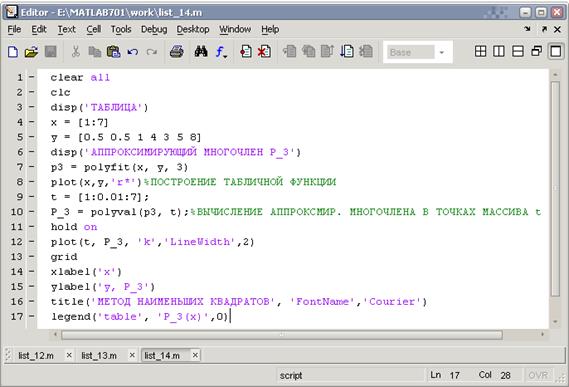
Графики табличной функции и аппроксимирующего многочлена

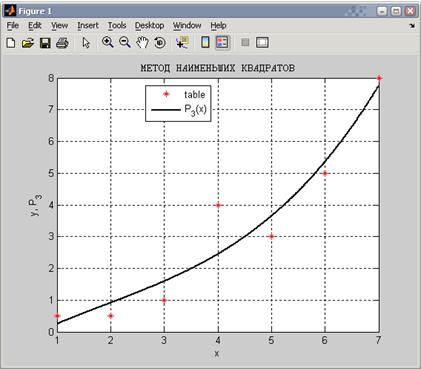
Вывод в командное окно

ТАБЛИЦА

x =

1 2 3 4 5 6 7

y =

0.5 0.5 1 4 3 5 8

АППРОКСИМИРУЮЩИЙ МНОГОЧЛЕН P_3

p3 =

0.027778 -0.16071 0.95437 -0.57143

Решение обыкновенных дифференциальных уравнений и систем

В MatLab существует функция ode45, которая реализует метод Рунге-Кутта 4-5 порядка

[X, Y] = ode45('name',[x0 b], y0),

где

name – функция, вычисляющая правую часть уравнения;

[x0 b]– интервал интегрирования дифференциального уравнения;

y0 – начальное условие;

X – массив координат узлов сетки, в которых ищется решение;

Y – массив значений искомой функции в этих узлах.

Как правило, размеры векторов X и Y достаточно велики, поэтому результат лучше отображать на графике.

А) Решение задачи Коши для обыкновенного дифференциального уравнения 1-го порядка:

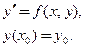
Пример.

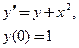на отрезке .

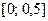Сначала создадим файл-функцию с двумя входными аргументами первым – x (переменной, по которой ведется интегрирование) и вторым – y (искомой функцией) и сохраним под именем fprdif:

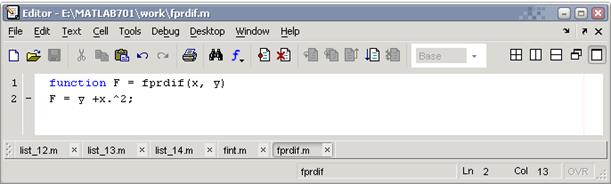
Создадим М-файл с именем list_15 для решения ОДУ:

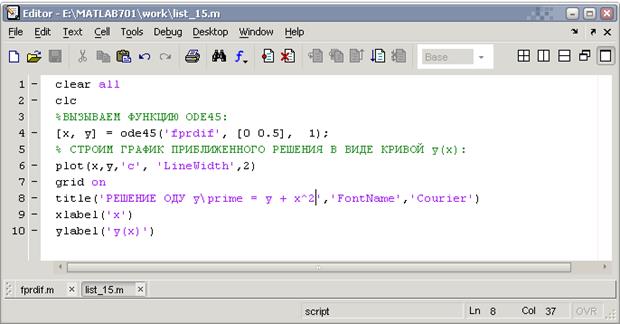
Результатом работы программы будет график

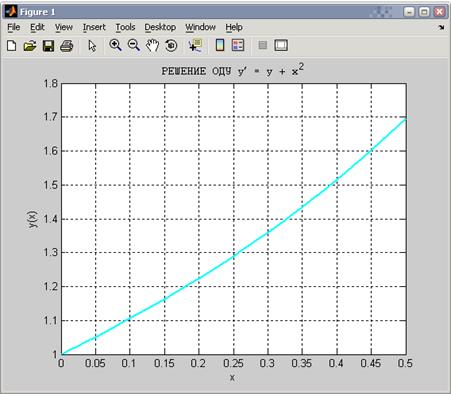
Б) Решение задачи Коши для систем ОДУ:

,

.

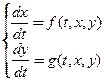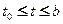
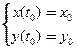Пример

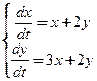с 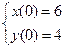на интервале .

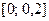Напишем файл-функцию с двумя входными аргументами: переменной 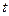, по которой ведется дифференцирование, и вектором 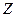, размер которого равен числу неизвестных функций системы: 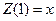, 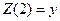. Выходным аргументом является вектор правой части системы. Имя функции fosl.

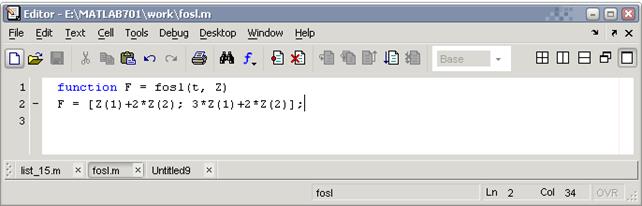
Далее, обращаемся к функции ode45 в отдельном М-файле list_16.

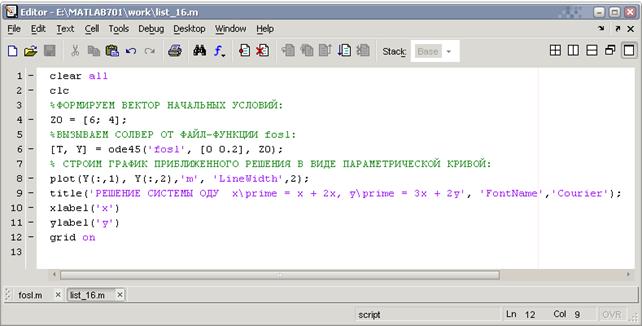
Результатом работы программы будет график

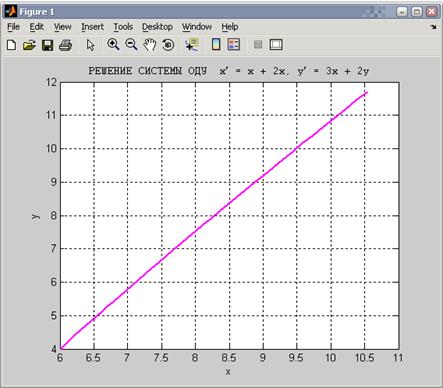
В) Решение задачи Коши для дифференциальных уравнений высших порядков:

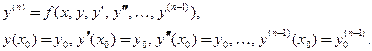
Алгоритм решения состоит в следующем

1. Приведение дифференциального уравнения к системе уравнений первого порядка.

2. Написание специальной файл-функции для правой части системы.

3. Вызов солвера ode45.

4. Визуализация результата.

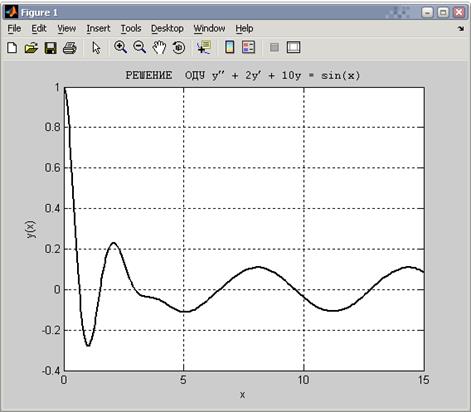
Пример

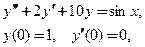на отрезке .

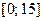Приведем исходное уравнение к системе дифференциальных уравнений. Для этого надо ввести столько вспомогательных функций, каков порядок уравнения. В данном случае введем две вспомогательные функции:

.

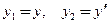Тогда получим систему дифференциальных уравнений

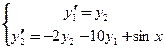
с начальными условиями

.

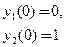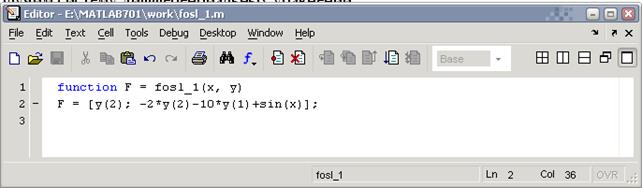
Сначала создаем функцию fosl_1 вычисления правой части системы, в которой принято обозначение: x – переменная интегрирования, y – вектор с элементами , :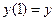

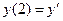Затем напишем программу list_17 в которой используется солвер ode45для решения системы соответствующей исходному дифференциальному уравнению:

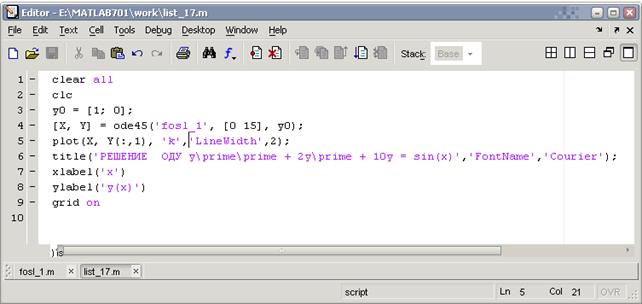
В результате выполнения программына экран выводится график приближенного решения

Решение краевой задачи

Рассмотрим решение краевой задачи общего вида для обыкновенного дифференциального уравнения второго порядка. Пусть требуется решить уравнение второго порядка

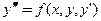
на отрезке 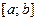, причем решение должно удовлетворять следующим условиям на границе отрезка

,

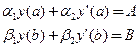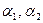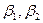
где , , 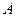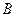– заданные числа.

Решение задачи состоит их нескольких этапов:

1. Преобразование уравнения второго порядка к системе двух уравнений первого порядка. Для этого вводим две вспомогательные функции:

.

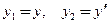1. Написание файл-функции для вычисления правой части системы.
2. Написание файл-функции, определяющей граничные условия. При этом граничные условия требуется записать так, чтобы в правых частях стояли нули:

.

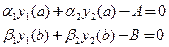Файл-функция должна иметь два входных аргумента, каждый из которых является век тором значений неизвестных функци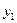й и 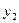в начальной и конечной точках промежутка.

1. Формирование начального приближения при помощи функции bvpinit. Аргументами функции bvpinitявляются вектор с координатами узлов сетки 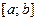и вектор, состоящий из двух элементов, содержащий начальное приближение.
2. Вызов солвера bvp4c для решения граничной задачи. MatLab находит приближенное решение методом конечных разностей и в результате получается вектор значений функции в точках отрезка (узлах сетки).
3. Графическое изображение результата.

Пример

.

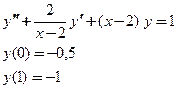Здесь , , , , , .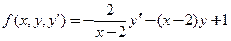

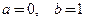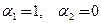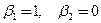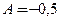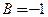Введем две вспомогательные функции:

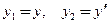
и получим систему дифференциальных уравнений и граничные условия для неё

.

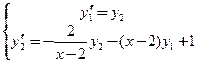
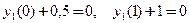Напишем файл-функцию rside для правой части системы уравнений:

------------------------------------------------------------------------------------------------------------------------

function f = rside(x, y)

f = [y(2); -2*y(2)./(x-2)-(x-2).*y(1)+1];

------------------------------------------------------------------------------------------------------------------------

Напишем файл-функцию boundдля правой части системы уравнений:

------------------------------------------------------------------------------------------------------------------------

function f = bound(ya, yb)

f = [ya(1)+0.5; yb(1)+1];

------------------------------------------------------------------------------------------------------------------------

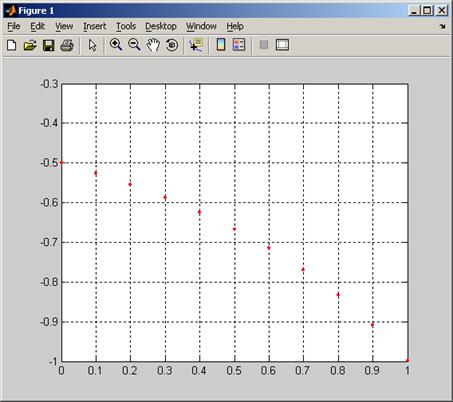
Решение граничной задачи оформим в виде файл-программы, в которой зададим начальное приближение при помощи bvpinit и вызовем солвер bvp4c для получения приближенного решения, затем построим график приближенного решения в виде множества точек.

------------------------------------------------------------------------------------------------------------------------

% РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ.

clear all

% ВВОДИМ СЕТКУ С ШАГОМ 0.1:

X0 = [0:0.1:1];

% ФОРМИРУЕМ НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ:

Y0 = [0 0];

initsol = bvpinit(X0, Y0);

% ВЫЗЫВАЕМ СОЛВЕР BVP4C:

sol = bvp4c('rside', 'bound', initsol);

% CТРУКТУРА sol:

% sol.x – ВЕКТОР, В КОТОРМ СОДЕРЖАТЬСЯ КООРДИНАТЫ УЗЛОВ СЕТКИ

% sol.y – МАТРИЦА, СОСТОЯЩАЯ ИЗ ДВУХ СТРОК,

% sol.y(1, :) – СООТВЕТСТВУЕТ ЗНАЧЕНИЯМ ФУНКЦИИ y1

% sol.y(2, :) - СООТВЕТСТВУЕТ ЗНАЧЕНИЯМ ФУНКЦИИ y2

plot(sol.x, sol.y(1,:), 'r.')

grid on

------------------------------------------------------------------------------------------------------------------------