Решение обыкновенных дифференциальных уравнений. Задача Коши

Существует множество технических систем и технологических процессов, характеристики которых непрерывно меняются со временем t. Такие явления обычно подчиняются физическим законам, которые формулируются в виде дифференциальных уравнений.

Дифференциальными называются уравнения, содержащие одну или несколько производных. Лишь очень немногие из них удаётся решить без помощи вычислительной техники. Поэтому численные методы решения дифференциальных уравнений играют важную роль в практике инженерных расчётов.

В зависимости от числа независимых переменных и типа входящих в них производных дифференциальные уравнения делятся на две существенно различные категории: обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называются частными. В этой главе рассматриваются методы решения обыкновенных дифференциальных уравнений.

Постановка задачи

Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если эти дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши. Часто в задаче Коши в роли независимой переменной выступает время.

Задачу Коши можно сформулировать следующим образом.

Пусть дано дифференциальное уравнение 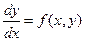и начальное условие y(x₀) = y₀. Требуется найти функцию y(x), удовлетворяющую как указанному уравнению, так и начальному условию.

Численное решение задачи Коши сводится к табулированию искомой функции.

График решения дифференциального уравнения называется интегральной кривой.

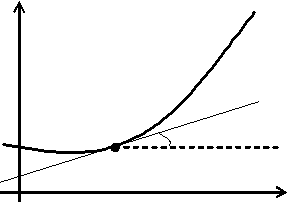
Геометрический смысл задачи:

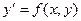- тангенс угла наклона касательной к графику решения в точке (x, y) к оси ОХ, - угловой коэффициент (рис.1).

x

а tg(α) = f(x, y)

y

Существование решения:

Если правая часть f(x,y) непрерывна в некоторой области R, определяемой неравенствами

|x – x₀| < a ; |y – y₀| < b

то существует, по меньшей мере, одно решение y = y(x), определённое в окрестности |x – x₀| < h, где h – положительное число.

Это решение единственно, если в R выполнено условие Липшица

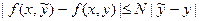
где N – некоторая постоянная (константа Липшица), зависящая, в общем случае, от a и b. Если f(x, y)имеет ограниченную производную 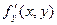в R, то можно положить

N = max| 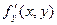| при 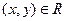.