Исследование функций и построение графиков функций.
I. Цели и задачи занятия
1. Рассмотреть схему исследования функций и построения графиков функций.
2. Воспитывать у обучающихся стремление к углубленному освоению материала по теме занятия, расширению профессионального кругозора, обучению методам самостоятельной работы с первоисточниками и учебными материалами.
3. Проверить качество усвоения обучающимися учебного материала.
II. План проведения и расчет учебного времени
| Содержание и порядок проведения занятия | Время, мин |
| ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы: 1. Схема исследования графиков функций. 2. Исследование функций и построение графиков функций. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ |
III. Учебно-материальное обеспечение
Классная доска, раздаточный материал, плакат с таблицей производных, планшет, видеопроектор, экран.
IV. Методические материалы
К проведению практического занятия
Во вводной части занятия (5 мин) после объявления темы и целей практического занятия целесообразно изложить последовательность обсуждения учебных вопросов.
Первый учебный вопрос (10 мин).
Схема исследования графиков функций.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями координат.
3 Найти интервалы знакопостоянства функции (промежутки, на которых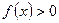 
и 
).
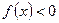4. Выяснить, является ли функция четной, нечетной или общего вида.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности и экстремумы функции.
7. Найти интервалы выпуклости и точки перегиба графика функции.
8. Построить график функции.
Второй учебный вопрос (70 мин).
Исследование функций и построение графиков функций.
Решение упражнений:
Решение:
№ 1. Исследуйте функцию и постройте ее график: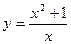 
.
Решение:
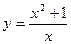
1) 
;
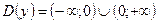2) Точек пересечения с осью Оy нет, т.к.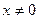 
.
Точки пересечения с осью Ox: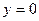 
, 
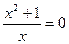, т.к. 
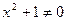, то пересечений с осью Ox нет.
3) 
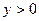, если 
; 
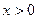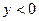, если 
.
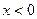4) 
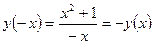=> функция нечетная, непериодическая.
5) Асимптоты (см. 4 а):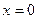 
– вертикальная асимптота.
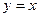– наклонная асимптота.
6) Монотонность (см. 1 в):
;
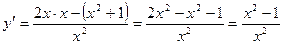Кр. точки: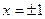 
; .
 |  |  |  |  |  | ||
 | + | – | – | – | + | ||
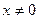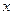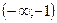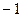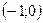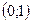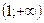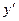Поведение 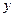 | 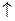 | max |  | – | | Min | |
| Значение |  | – |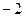
7) Выпуклость (см. 1 в):
.
=> 
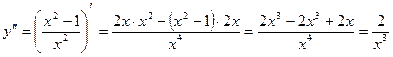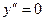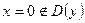, следовательно, критических точек нет.
| |  |  |
 | – | + |
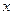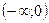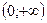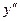| Поведение |  |  |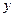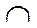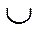
| Значение |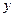
Построим график функции:
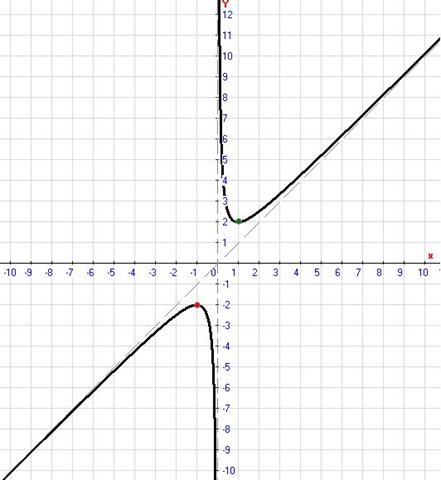
№ 2. Исследуйте функцию и постройте ее график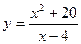 
.
Решение:
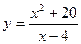
1) 
;
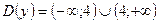2) Точки пересечения с осями:
Oy: =>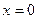 
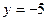, точка пересечения: 
;
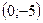Ox: =>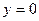 
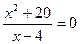, т.к. 
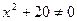. то точек пересечения с осью Ox нет.
3) 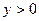, т.к. 
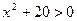, то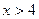 
; => 
.
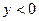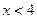4) 
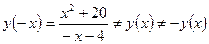=> функция не является ни четной ни нечетной.
5) Асимптоты: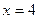 
– точка разрыва 2-го рода; 
; 
;
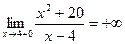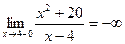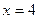– вертикальная асимптота.
;
.
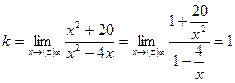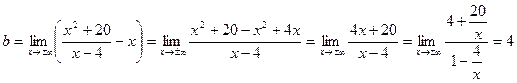Наклонная асимптота: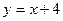 
.
6) Монотонность:
.
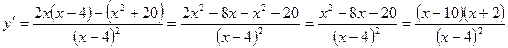Кр. точки: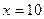 
; 
; 
.
| |  | |  |  |  | ||
| | + | – | – | – | + | ||
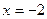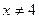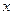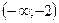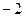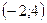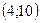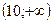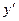| Поведение 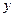| 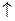| max | 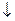| – | 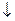| min | |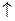
| Значение |  | – |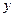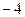
7) Выпуклость:
.
=> 
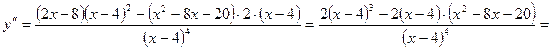
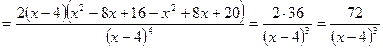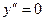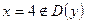, следовательно, критических точек нет.
| |  |  |
| | – | + |
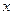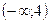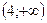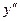| Поведение | | |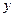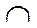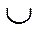
| Значение |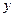
Построим график функции:
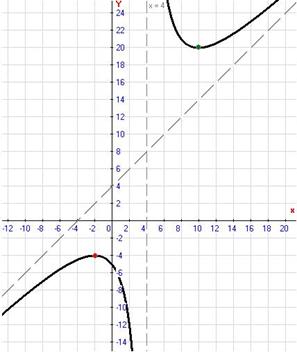
№ 3. Исследуйте функцию и постройте ее график:
1) 
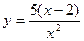; 2) 
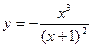; 3)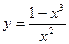 
.
Решение:
1) .
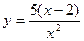1. Область определения: ;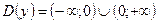
2. Точки пересечения с осями:
Точек пересечения с осью Оy нет, т.к. .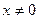
Точки пересечения с осью Ox: ,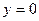 
=> 
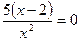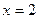. Точка пересечения: 
.
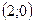3. Промежутки знакопостоянства:
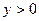, если 
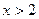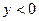; , если 
.
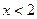4. Четность: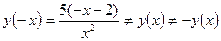 
=> функция не является ни четной ни нечетной.
5. Асимптоты: 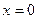– точка разрыва второго рода.
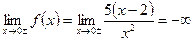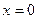=> – вертикальная асимптота.
; 
=>
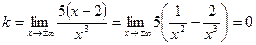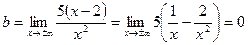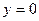– горизонтальная асимптота.
6. Монотонность:
.
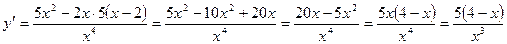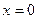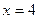, – кр. точки, 
.
| | |  | | |
| | – | + | – | |
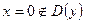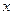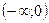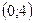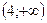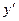| Поведение 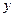| 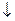| 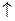| max | |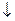
| Значение |  |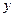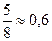
7. Выпуклость:
.
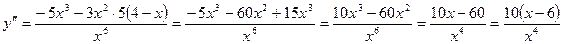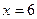– кр. точки, .
| | |  |  | |
| | – | – | + | |
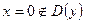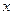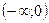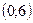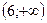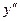| Поведение 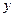| 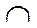| 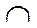| перегиб | |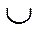
| Значение |  |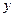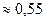
Построим график функции:
2)
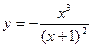
1. Область определения: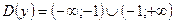 
;
2. Точки пересечения с осями:
Oy: 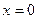; ; 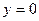Ox: ; .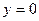
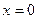Точка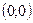 
– точка пересечения с осями координат.
3. Промежутки знакопостоянства:
: 
=> 
=> 
=> ;
: 
=> 
=> 
=> .
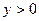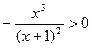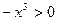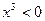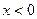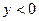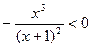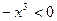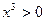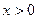4. Четность: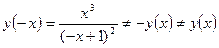 
=> Функция не является ни четной ни нечетной.
5. Асимптоты: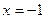 
– точка разрыва функции, 
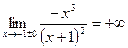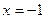=> – вертикальная асимптота;
;
;
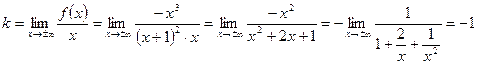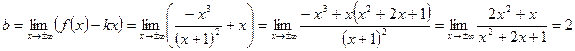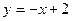– наклонная асимптота.
6. Монотонность:
;
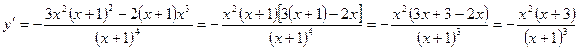Кр. точки: ;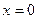 
; ( 
).
| |  |  |  | | | | |
| | – | + | – | – | – | ||
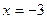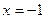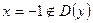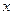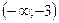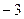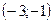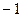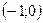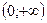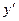| Поведение 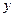| 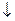| min | | – | | – | |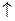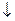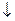
| Значение |  | – |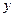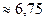
7. Выпуклость:
;
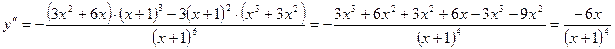Кр. точки: ; ( ).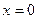
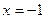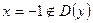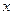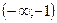| | | –1 | | | |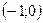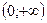
| | + | – | + | – | |
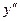| Поведение 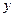| 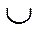| – | 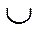| перегиб | |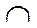
| Значение | – |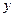
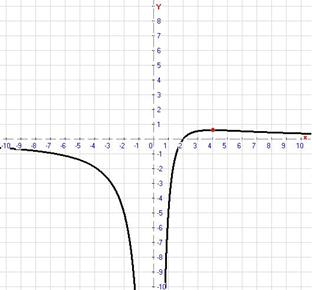
Построим график функции:
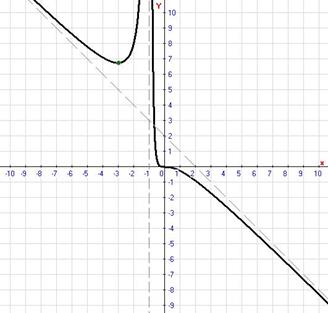
3) ;
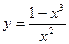1. Область определения: ;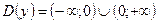
2. Точки пересечения с осями:
Точек пересечения с осью Оy нет, т.к. .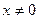
Точки пересечения с осью Ox: ,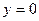 
=> 
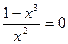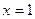. Точка пересечения: 
.
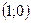3. Промежутки знакопостоянства:
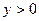, если 
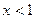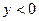; , если 
.
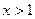4. Четность: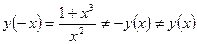 
=> Функция не является ни четной ни нечетной.
5. Асимптоты: 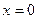– точка разрыва функции; 
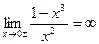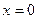=> – вертикальная асимптота;
; 
;
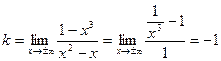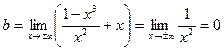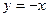– наклонная асимптота.
6. Монотонность:
;
: 
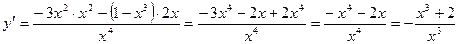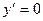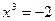, Кр. точка: 
, .
| |  |  |  | |
| | – | + | – | |
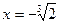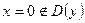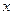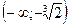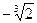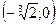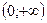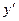| Поведение 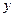| 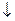| min | | |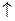
| Значение |  |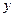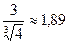
7. Выпуклость:
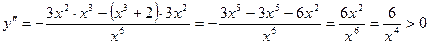=> функция выпукла вниз на всей области определения.
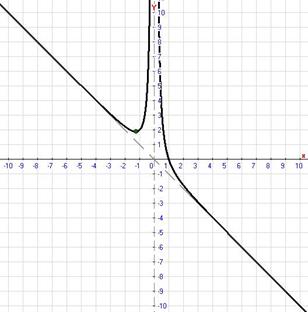
Построим график функции:
В заключительной части (5 мин)преподаватель подводит итоги и завершает работу практического занятия, давая оценку ходу занятия и работе отдельных обучающихся, ставя задачи на дальнейшее изучение учебной дисциплины. Здесь же необходимо дать характеристику последующих тем, указав, где будут использоваться обсужденные материалы, выдать задание на следующее занятие.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ
Повторить материалы занятия по конспекту, [8], с. 30 – 32.
№ 1[8], с.43, № 5 (5,6).
V. Литература
основная
1. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2010.
дополнительная
2. Шипачев В.С. Задачник по высшей математике. – М.: Высшая школа, 2009.
3. Старостина Е.В., Фомичев Д.С. Приложения производной к исследованию функции. – Иваново: ООНИ ИвИ ГПС МЧС России, 2010.-50 с.
Разработал: начальник кафедры
полковник вн. службы Е.Г. Родионов
Разработал: ст. преподаватель кафедры
капитан вн. службы Е.А. Шварев
«31» июля 2014 года