Раскрытие неопределенностей других видов по правилу Лопиталя
Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 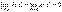 или
или 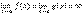 . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций 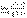 , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
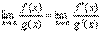 | (1) |
Таким образом, правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
17.4 Теорема: Достаточный признак возрастания функции.
Если f’(x)>0, (a,b), то f(x) возрастает на [a,b].
Док-во:
возьмем x1, x2 Î[a,b]: x1<x2 => f(x2)>f(x1)
применим т. Лангранжа f(x) на [x1,x2]
по этой теореме f(x2)-f(x1)=f’(c)(x2-x1)>0 => f(x2)>f(x1).Замечание: данные условия не являются необходимыми.
Теорема: достаточный признак убывания функции. Если f’(x)<0 на (a,b), то f(x) убывает на [a,b].
Док-во 1:подобно предыдущему.
Док-во 2:g(x)=-f(x),тогда g’(x)=-f’(x)>0
=> g(x) - возрастает => f(x) – убывает.
Несложно показать, что если функция возрастает (убывает) на [a,b], то ее произв. не отрицат.(положит.) на (a,b).
f(x) возрастает: [a,b]=>f’(x)Ê0 (a,b).
18.4Достаточные условия существования экстремума.
Если f’(x)>0 на интервале (x0-б,х0) и f’(x)<0 на интервале (х0,x0+б) т.е. меняет знак с плюса на минус при переходе на точку х0, т.е. х0 – точка максимума f(x), а если же меняет знак с минуса на плюс, то х0 – точка минимума.
Доказательство:
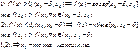
теорема: Второй достаточный признак максимума функции.
Если f(x) имеет непрерывную вторую производную в окрестности точки х0, и:
1). f’(x0)=0 2). f’’(x0)<0
то х0 точка максимума (аналогично, если f’’(x0)<0, то х0 – точка минимума)
Док-во: Возьмем окрестность, где вторая производная сохраняет знак и запишем формулу Тейлора 1-го порядка для х из данной окрестности.
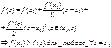
Выпуклость графика функции.
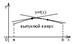 Опр. График функции y=f(x) называется выпуклым вниз (вверх) если он расположен выше (ниже) любой касательной проведенной к графику функции на данном интервале.
Опр. График функции y=f(x) называется выпуклым вниз (вверх) если он расположен выше (ниже) любой касательной проведенной к графику функции на данном интервале.
Теорема: Достаточный признак выпуклости графика функции вниз.
Если функция f(x) дважды дефференц. на нтервале (a,b) и ее вторая производн. f’’(x)>0 на интервале (a,b), то график функции y=f(x) выпуклый вниз на интервале (a,b).

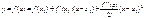 Уравнение касательной:
Уравнение касательной:
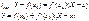
Возьмем X=x.Из первого вычтем второе
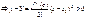
Поэтому y>Y следовательно график функции расположен выше касательной
Аналогично, если f’’(x)<0 на (a,b) то график функции y=f(x) - выпуклый вверх, на данном интервале.
Производная ф-и задана и параметрически
Пусть дана функция 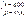 по определению
по определению
производной имеем 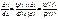
Производная параметрически заданной функции.
