Раскрытие неопределенностей

Вопрос 11

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В случае плоской задачи скалярное произведение векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Формула скалярного произведения n -мерных векторов

В случае n-мерного пространства скалярное произведение векторов a = {a₁ ; a₂ ; ... ; a_n} и b = {b₁ ; b₂ ; ... ; b_n} можно найти воспользовавшись следующей формулой:

a · b = a₁ · b₁ + a₂ · b₂ + ... + a_n · b_n

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:

a · a ≥ 0

2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:

a · a = 0 <=> a = 0

3. Скалярное произведение вектора самого на себя равно квадрату его модуля:

a · a = |a|²

4. Операция скалярного умножения коммуникативна:

a · b = b · a

5. Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b

6. (αa) · b = α(a · b)

7. Операция скалярного умножения дистрибутивна:

(a + b) · c = a · c + b · c

Вопрос №12

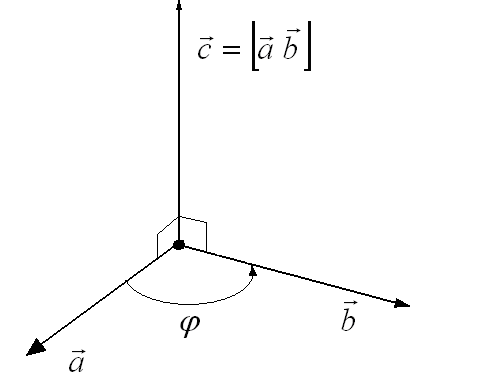
Векторное произведение

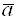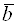Определение. Векторным произведением двух ненулевых, неколлинеарных векторов и называется вектор 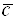обозначаемый 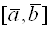и удовлетворяющий трем условиям:

1) 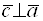и 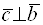(то есть 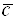перпендикулярен плоскости, определяемой векторами и , если они отложены от одной точки);

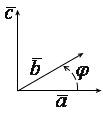2) 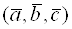– правая тройка (т. е., если 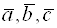приведены к общему началу, то из конца 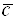поворот от вектора 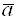к вектору 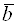на меньший угол виден происходящим против часовой стрелки);

3) 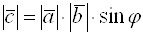, где .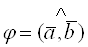

Заметим, что все условия в этом определении равноправны, т. е. нельзя отдавать предпочтение какому либо условию или пренебрегать любым из них.

Свойства векторного произведения.

1. .

2. 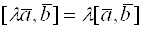, где 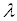– скаляр.

3. .

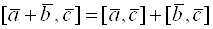4. – равен площади параллелограмма, построенного на приведенных к общему началу векторах 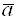и 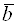. (Геометрический смысл векторного произведения.)

5. Для того, чтобы ненулевые векторы 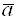И 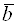были коллинеарны, необходимо и

достаточно, чтобы 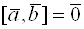. В частности .

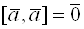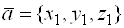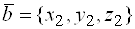6. Если заданы декартовы координаты векторов и , то 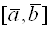можно представить в виде:

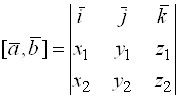. (13)

Вопрос №31

Производная функция - базовый элемент дифференциального исчисления, который является результатом применения какой-либо операции дифференцирования к исходной функции.

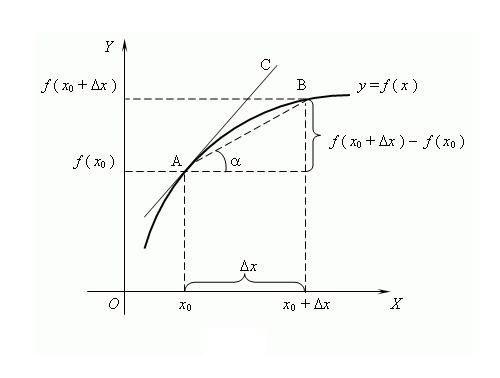
Название функции происходит от слова «произведенная», т.е. образованная от другой величины. Процесс определения производной какой-либо функции называется дифференцированием. Распространенный способ представления и определения - через теорию пределов, хотя она возникла позже дифференциального исчисления. Согласно этой теории производная - это предел отношения приращения функции к приращению аргумента, если такой предел существует, при условии, что аргумент стремится к нулю. Считается, что впервые термин «производная» употребил известный русский математик В.И.Висковатов.

Чтобы найти производную функции f в точке x, необходимо определить значения этой функции в точке х и в точке x+Δx, где Δx – приращение аргумента х. Найти приращение функции y = f(x+Δx) – f(x). Записать производную через предел отношения f’ = lim(f(x+Δx) – f(x))/Δx, вычислить при Δx → 0. Принято обозначать производную знаком апостроф «’» над дифференцируемой функцией. Один апостроф – первая производная, два – вторая, производная высшего порядка задается соответствующей цифрой, например, f^(n) – производная n-го порядка, где n – целое число ≥ 0.

Вопрос №27

Функция называется целочисленной или последовательностью, если область определения функции представляет собой множество натуральных чисел.

Обозначения: Последовательности обозначаются как {a_n}, {y_n}, члены последовательности как a_n, y_n.

Число b называется пределом последовательности{y_n}, если по мере возрастания n членy_nнеограниченно приближается к значению b:

.

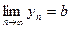Символ lim от латинского слово «limes» - предел.

Пример: Члены последовательности 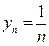по мере возрастания n стремятся к нулю: y₁ = 1; y₂ = 0,5; y₃ = 0,33¼; y₄ = 0,25; ¼; y₁₀₀ = 0,01; ¼; y₁₀₀₀ = 0,001; ¼ Следовательно, пределом последовательности является число 0:

.

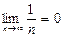Пример: Члены последовательности 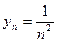по мере возрастания n стремятся к нулю, поэтому .

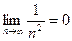Более строгое определение предела следующее.

Число b называется пределом последовательности {yn}, если абсолютная величина разности yn–b, начиная с некоторого номера N, остается меньшей любого заранее данного положительного числа e: |yn–b| < e при n ³ N (N зависит от величины e).

Последовательность, имеющая предел, называется сходящейся, в противном случае, она расходящаяся.

Свойства пределов

1. Постоянный множитель можно вынести за знак предела: .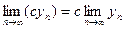

2. Предел суммы (разности) равен сумме (разности) пределов: .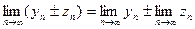

3. Предел произведения равен произведению пределов: .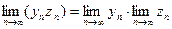

4. Предел отношения равен отношению пределов: 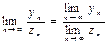, если .

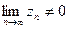Эти свойства справедливы не только для последовательностей, но и для функций y(x).

№13

Вопрос №39

Название функции	Формула функции	График функции	Название графика	Комментарий
Линейная	y = kx		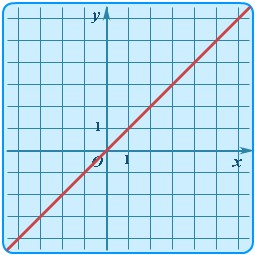Прямая	Cамый простой частный случай линейной зависимости - прямая пропорциональность у=kx, где k ≠ 0 - коэффициент пропорциональности. На рисунке пример для k =1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
Линейная	y = kx + b		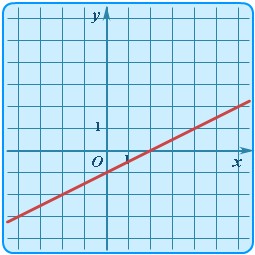Прямая	Общий случай линейной зависимости: коэффициенты k и b - любые действительные числа. Здесь k = 0.5, b = -1.
Квадратичная	y = x2		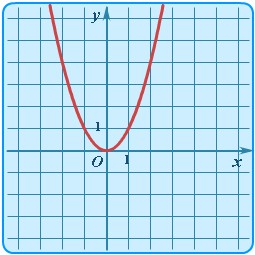Парабола	Простейший случай квадратичной зависимости - симметричная парабола с вершиной в начале координат.
Квадратичная	y = ax2 + bx + c		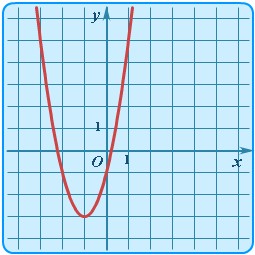Парабола	Общий случай квадратичной зависимости: коэффициент a - произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c - любые действительные числа.
Степенная	y = x3		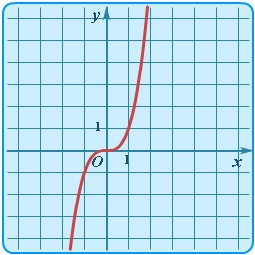Кубическая парабола	Самый простой случай для целой нечетной степени.
Степенная	y = x1/2		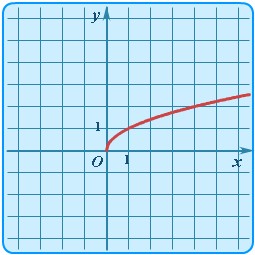График функции y = √x	Самый простой случай для дробной степени (x1/2 = √x).
Степенная	y = k/x		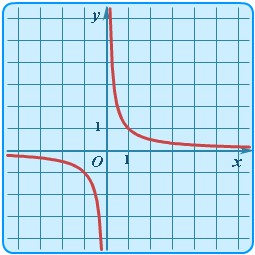Гипербола	Самый простой случай для целой отрицательной степени (1/x = x-1) - обратно-пропорциональная зависимость. Здесь k = 1.
Показательная	y = ex		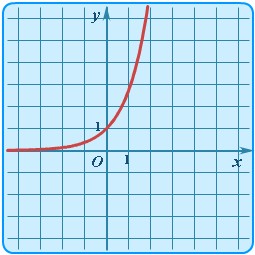Экспонента	Экспоненциальной зависимостью называют показательную функцию для основания e - иррационального числа примерно равного 2,7182818284590...
Показательная	y = ax		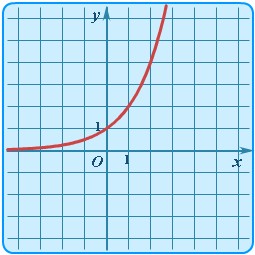График показательной функции	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1).
Показательная	y = ax		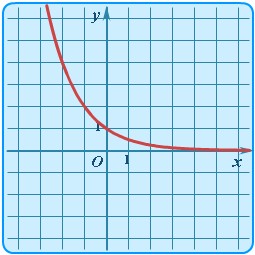График показательной функции	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1).
Логарифмическая	y = lnx		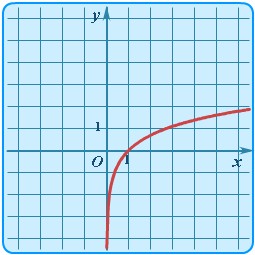График логарифмической функции	График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой.
Логарифмическая	y = logax		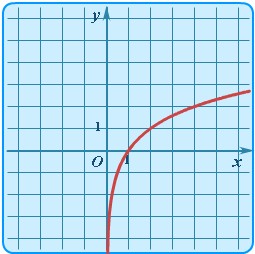График логарифмической функции	Логарифмы определены для a >0 и a ≠1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1).
Логарифмическая	y = logax		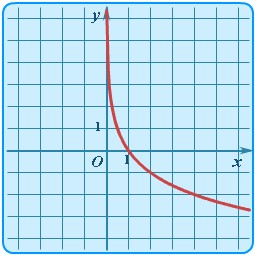График логарифмической функции	Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1).
Синус	y = sinx		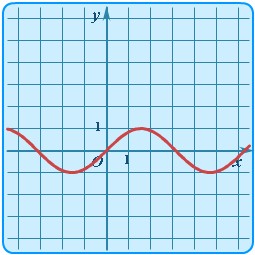Синусоида	Тригонометрическая функция синус.
Косинус	y = cosx		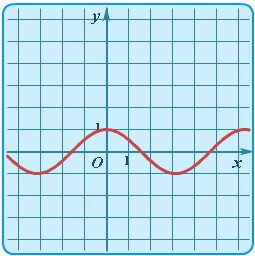Косинусоида	Тригонометрическая функция косинус.
Тангенс	y = tgx		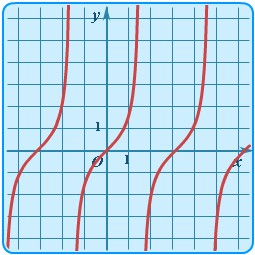Тангенсоида	Тригонометрическая функция тангенс.
Котангенс	y = сtgx		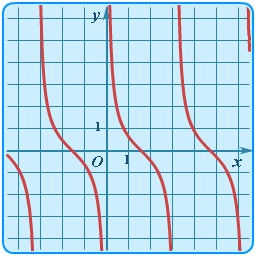Котангенсоида	Тригонометрическая функция котангенс.

Обратные тригонометрические функции.
Название функции	Формула функции	График функции	Название графика	Комментарий
Арксинус	y = arcsinx		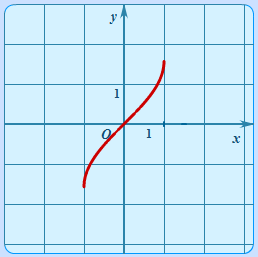График арксинуса	Тригонометрическая функция обратная к y = sinx.Определена на отрезке [−1; 1]. Принимает значения от −π/2 до π/2.
Арккосинус	y = arccosx		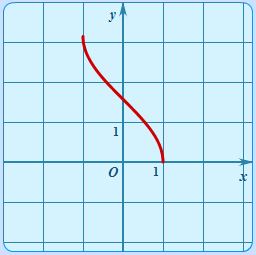График арккосинуса	Тригонометрическая функция обратная к y = cosx.Определена на отрезке [−1; 1]. Принимает значения от 0 до π.
Арктангенс	y = arctgx		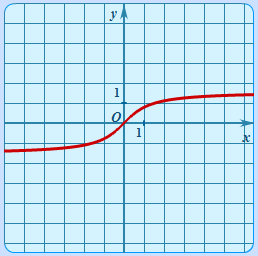График арктангенса	Тригонометрическая функция обратная к y = tgx.Определена на множестве действительных чисел. Принимает значения на интервале (−π/2; π/2). Имеет асимптоты.
Арккотангенс.	y = arcctgx		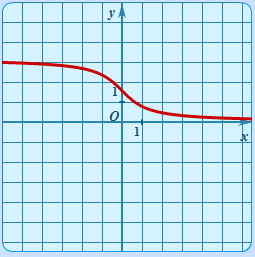График арксинуса	Тригонометрическая функция обратная к y = ctgx.Определена на множестве действительных чисел. Принимает значения на интервале (0 π). Имеет асимптоты.

Вопрос №20

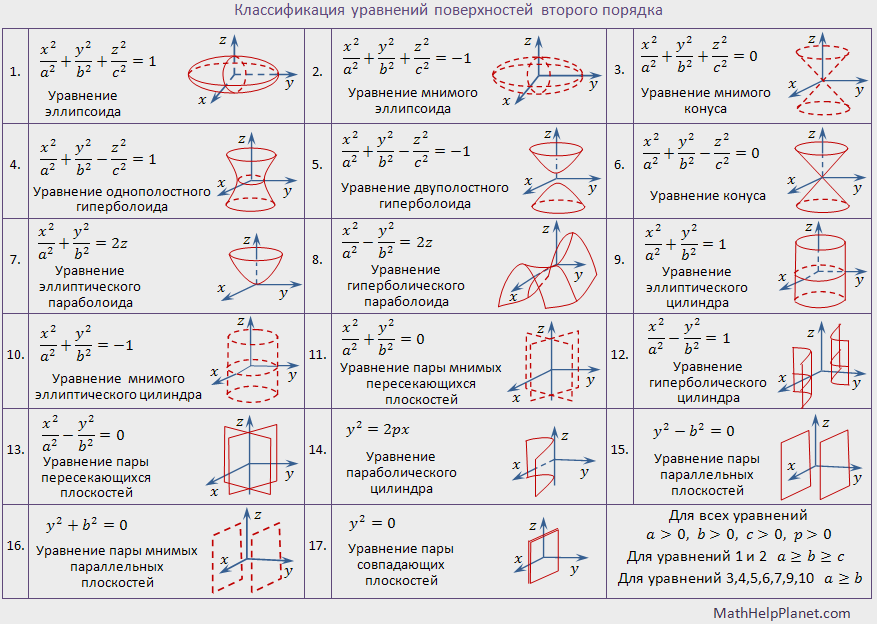
Вопрос №19

Вопрос №29

Эквивалентность функций. Таблица эквивалентных бесконечно малых функций, вычисление пределов. Односторонние пределы

Функции 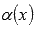и 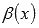называют бесконечно малыми при 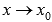, есл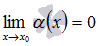и и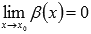

Определение

Б.м. функции 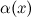и 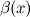называются эквивалентными или равносильными б.м. одного порядка при 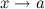, если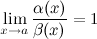

Обозначают: 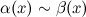при .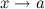

Пример

Задание. Проверить, являются ли функци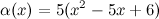и и 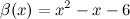эквивалентными бесконечно малыми при .

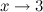Решение. Проверим вначале, что данные функции являются бесконечно малыми функциями в точке :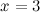

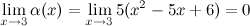
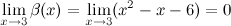
Найдем предел отношения этих функций:

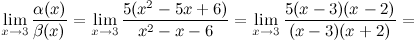
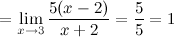
Ответ. Заданные функци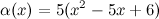и и 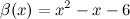являются эквивалентными бесконечно малыми.

Таблица эквивалентных б.м. функций

Таблица эквивалентных б.м. функций при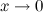

Вопрос №28

Основные виды неопределенностей:

, , , , , ,

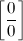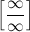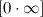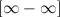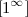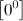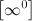
Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение.

Раскрытие неопределенностей

Для раскрытия неопределенностей используют следующее:

· упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;

· замечательные пределы - первый замечательный предел и второй замечательный предел;

· правило Лопиталя;

· эквивалентные бесконечно малые функции.

Первый замечательный предел: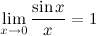

Второй замечательный предел: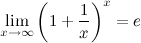

Вопрос №24