Правило Лопиталя для неопределенностей вида 0/0

Теорема Ролля (о корнях производной)

Пусть функция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и значения функции на концах отрезка равны f(a) = f(b). Тогда на интервале (a;b) существует точка с, a < c < b, в которой производная функции f(x) равна нулю, т.е. f `(c)=0

Д-во:

По свойству неопределенных функций на отрезке функция f(х) принимает на отрезке [a;b] наибольшее и наименьшее значение, обозначим соответственно M,m.

1) M=m => f(x) = M = m - f(x) = c – const, f `(x) = c` = 0.

2) M≠m => f(a) = f(b).

Пусть M или m – достигается во внутренней точке. По теореме Ферма, f `(c) = 0.

Теорема Лагранжа

Пусть функция f(x) непрерывна на отрезке [a;b] , дифференцируема на всем интервале (a;b) . Тогда на (a;b) существует точка с , a < c < b, такая, что (f(b) – f(a))/ (b - a) = f `(c) или f(b) – f(a) = f `(c) (b-a).

Д-во:

Рассмотрим вспомогательную функцию

F(x) = [f(x) – f(a)] - 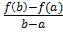(x-a).

Она

a) a)определена и непрерывна на [a;b], так как функция f(x) непрерына на [a;b];

b) существует F`(x):

F`(x) = f `(x) – [ ].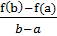

c) F(a) = F(b) = 0.

Таким образом, для F(x) выполнены все условия теоремы Ролля. Действительно, она непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Нетрудно проверить, подставляя x=a и x=b , что F(a) = 0 и F(b) = 0, т.е. F(a) = F(b). Поэтому и существует с принадлежащая [a;b] такая, что

F`(c) = f `(c) – [ 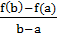]=0.

Но когда в этой точке с

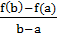= f `(c),

что и дает формулу Лагранжа.

Теорема Коши

Пусть функции f(x) и g(x) непрерывны на отрезке [a;b], дифференцируемы на интервале (a;b) и g(x) ≠ 0 на интервале (a;b). Тогда существует точка с, a< c < b, такая, что

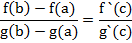
Д-во:

g(a) ≠ g(b) (т.к. по теореме Ролля существует с | g `(c) =0).

Рассмотрим функцию F(x) = [f(x) – f(a)] – 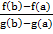*[g(x)-g(a)]

1) Функция определена и непрерывна на [a;b];

2) Существует F `(x) = f `(x) – 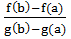* g `(x);

3) F(a) = F(b) = 0

F(x) – удовлетворяет теореме Ролля

Существует c принадлежащая (a;b) | F `(c) = f `(c)- 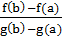* g `(c) =>

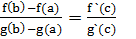g(x) = x

Теорема о дифференцируемости параметрически заданной функции

Если функция аргумента х задана параметрически:

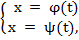α ≤ t ≤ β,

Где φ(t) и ψ(t) – дифференцируемые функции, причем φ`(t) ≠ 0, то производная этой функции по переменной х вычисляется по формуле

_.

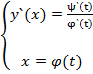Док-во:

Пусть 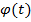и 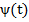– дифференцируемы и 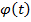≠ 0. Кроме того, будем считать, что функция х = 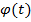имеет обратную функцию t = φ ^-1(x), которая также дифференцируема. Тогда функцию, заданную параметрически, можно рассматривать как

y = ψ(t), t = φ ^-1(x),

считая t промежуточным аргументом.

Продифференцируем функцию y = ψ(t), t = φ ^-1(x) по правилу дифференцирования сложной функции, получим

y`(x) = ψ`(t)*t`(x).

Производную t`(x) найдем по правилу дифференцирования обратной функции:

t`(x) = .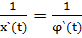

Итак, окончательно имеем: если 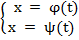, то .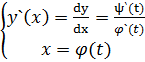

Правило Лопиталя для неопределенностей вида 0/0

Пусть a принадлежит R и выполнены 2 условия:

1) Функции f(x) и g(x) определены и непрерывны в U(a,б) или U*(a,б);

2) В U(a,б) или U*(a,б) существуют f `(x) и g`(x), причем при любом x принадлежащем U*(a,б) g`(x) ≠ 0;

3) 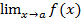= = 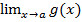0;

4) Существует 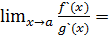k.

Тогда существует 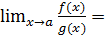k.

Док-во:

Докажем это утверждение для a принадлежащего R.

1)Пусть x принадлежит U*(a,б). Для точки a возможны 2 случая:

а)функции f(x) и g(x) непрерывны в точке a. Тогда из условия получаем f(a)=g(a)=0.

b) Пусть x принадлежит U*(a,б), функции f(x) и g(x) разрывны в точке a. Тогда точка a – точка устранимого разрыва 1 рода. Доопределим функции, полагая f(a)=g(a)=0. Таким образом можно считать, что f(x) и g(x) непрерывны в U(a,б).

2) Пусть Пусть x принадлежит U(a,б). Рассмотрим функции f(x) и g(x) на [a;x] (или [x;a]). Они удовлетворяют теореме Коши. Тогда по формуле Коши

=

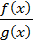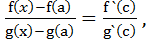
Где a < c < x (или x < c < a). Поэтому при x -> a также будет c -> a. Переходя к пределу, получим

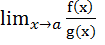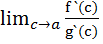= = k,

Так как последний предел существует.