Раскрытие неопределенностей. Правило Лопиталя
К разряду неопределенностей принято относить следующие соотношения:
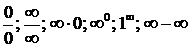
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует:
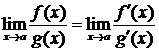
Пример. Найти предел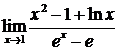 
.
◄ Как видно, при попытке непосредственного вычисления предела получается неопределенность вида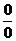 
. Функции, входящие в числитель и знаменатель дроби, удовлетворяют требованиям теоремы Лопиталя.
f¢(x) = 2x + 
; g¢(x) = ex;
. ►
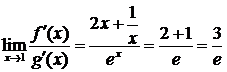Пример. Найти предел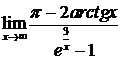 
.
◄ 
; 
;
.►
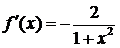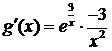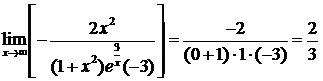Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
Пример. Найти предел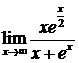 
.
◄ 
; 
;
; 
;
; 
; 
.►
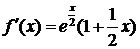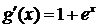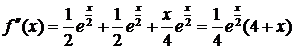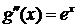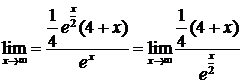
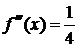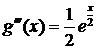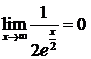Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).
Пример. Найти предел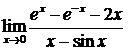 
.
◄ 
; 
;
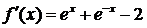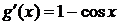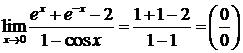- опять получилась неопределенность. Применим правило Лопиталя еще раз:
; 
;
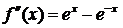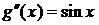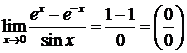- применяем правило Лопиталя еще раз.
; 
;
. ►
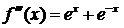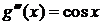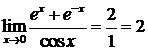Неопределенности вида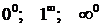 
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 
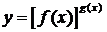, f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
Пример. Найти предел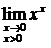 
.
◄ Здесь y = xx, lny = xlnx.
Тогда 
. Следовательно 
. ►
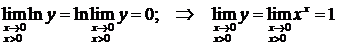Пример. Найти предел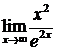 
.
◄ 
; 
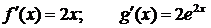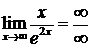- получили неопределенность. Применяем правило Лопиталя еще раз:
.►
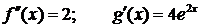
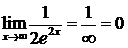Лекция 9.2 «Исследование функций и построение графиков»
Учебные вопросы:
1. Экстремумы
2. Выпуклость и вогнутость. Асимптоты
3. Общая схема исследования функций и построения графиков
Экстремумы
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка X, то функция возрастает на этом промежутке.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой функции отрицательна внутри некоторого промежутка X, то функция убывает на этом промежутке.
Необходимое условие монотонности более слабое: если функция возрастает (убывает) на некотором промежутке X, то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке: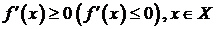 
, т.е. в отдельных точках производная монотонной функции может равняться нулю.
Например, функция y=x3 монотонно возрастает на всей числовой оси, но при x=0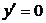 
Точка x0 называется точкой максимума функции ƒ(x),если в некоторой окрестности точки x0 выполняется неравенство ƒ(x0) ≥ ƒ(x).
Точка x1 называется точкой минимума функции ƒ(x), если в некоторой окрестности точки x1 выполняется неравенство ƒ(x1) ≤ ƒ(x).
Значения функции в точках x0 и x1 называются соответственно максимумом и минимумом функции. Их объединяют общим названием экстремума функции. Его также называют локальным экстремумом, поскольку понятие экстремума связано лишь с достаточно малой окрестностью точки x0. На одном промежутке функция может иметь несколько экстремумов, причем минимум в одной точке может оказаться больше максимума в другой точке (см. рис.).
 |
Если в точке x0 дифференцируемая функция имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма. Следовательно,
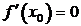. Но функция может иметь экстремум и в точках, в которых она не дифференцируема (см. рис.).
|
 |
Отсюда необходимое условие экстремума: для того, чтобы функция y=f(x) имела экстремум в точке x0, необходимо, чтобы её производная в этой точке равнялась нулю или не существовала.
(Экстремум в точке x =0, но функция здесь не дифференцируемая)
|
 |
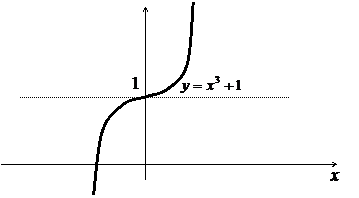(Производная равна нулю при x=0, но экстремума нет)
Точки, в которых выполнено необходимое условие экстремума, называются критическими (стационарными).
Теорема (первое достаточное условие экстремума). Если при переходе через точку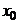 
производная дифференцируемой функции меняет свой знак с плюса на минус, то точка 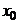есть точка максимума функции y=ƒ(x), а если с минуса на плюс, то точка минимума.
Схема исследование функции y=ƒ(x) на экстремум:
1. Найти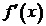 
.
2. Найти критические точки функции, в которых 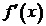=0 или не существует.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4. Найти экстремумы функции (экстремальные значения функции).
Теорема (второе достаточное условие экстремума). Если функция ƒ(x)дважды дифференцируема и в некоторой точке x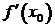0 
=0,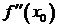 
>0, то x0 есть точка минимума функции y=ƒ(x),если 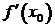=0, 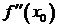<0, то точка максимума.
Для отыскания наибольшего и наименьшего значений функции наотрезкенадо найти значения функции в критических точках и на концах отрезка и выбрать из них наименьшее и наибольшее значение.
Если функция непрерывна на интервале (а, b), то она может и не принимать на нем наибольшего и наименьшего значений. В частности, если дифференцируемая функция на интервале (а, b) имеет лишь одну точку максимума, то наибольшее значение функции совпадает с максимумом этой функции.