Исследование функций и построение графиков
Введение
Производная находит широкое применение при решении различных задач. В настоящей методической работе приведен необходимый материал без доказательства, который проиллюстрирован примерами. Далее приведены примеры для самостоятельного решения. Нами рассмотрены теоремы Ролля, Лагранжа, Коши. Теоремы Лопиталя-Бернули для раскрытия неопределенностей при вычислении пределов, формула Тейлора и применение производной для исследования функций.
Для понимания материала и решения задач студенту необходимо знать таблицу производных и правила дифференцирования функций. Методическая работа может быть использована студентами и преподавателями на практических занятиях по данной теме.
Теоремы Ролля, Лагранжа, Коши
Теорема Ролля. Если функция 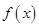 непрерывна на отрезке
непрерывна на отрезке 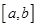 , дифференцируема в интервале
, дифференцируема в интервале 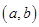 и на концах отрезка принимает равные значения, т.е.
и на концах отрезка принимает равные значения, т.е. 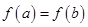 , то существует точка
, то существует точка 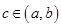 такая, что
такая, что 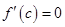 . Точки, в которых
. Точки, в которых 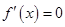 , называются стационарными точками функции
, называются стационарными точками функции 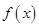 .
.
Теорема Лагранжа. Если функция 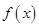 непрерывна на отрезке
непрерывна на отрезке 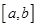 , дифференцируема в интервале
, дифференцируема в интервале 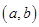 , то существует точка
, то существует точка 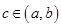 такая, что справедливо равенство
такая, что справедливо равенство
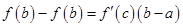 .
.
Теорема Коши. Если функции 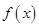 и
и 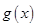 непрерывны на отрезке
непрерывны на отрезке 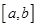 , дифференцируемы в интервале
, дифференцируемы в интервале 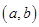 и
и 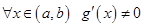 , то существует точка
, то существует точка 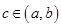 такая, что
такая, что
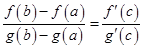 .
.
Решить следующие задачи:
1. Функция 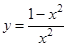 имеет на концах отрезка
имеет на концах отрезка 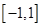 равные значения (проверьте). Производная данной функции в интервале
равные значения (проверьте). Производная данной функции в интервале 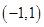 не обращается в нуль ни в одной точке (проверьте). Какие условия Теоремы Ролля для данной функции на отрезке
не обращается в нуль ни в одной точке (проверьте). Какие условия Теоремы Ролля для данной функции на отрезке 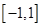 не выполнены?
не выполнены?
2. Пусть 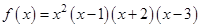 . Показать, что три корня уравнения
. Показать, что три корня уравнения 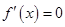 действительны.
действительны.
3. Доказать, что уравнение 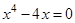 не имеет корней в интервале
не имеет корней в интервале 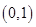 .
.
4. Пусть 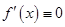 в интервале
в интервале 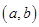 . Доказать, что
. Доказать, что 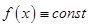 на
на 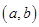 .
.
5. Пусть 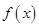 и
и 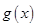 удовлетворяют всем условиям Теоремы Коши на
удовлетворяют всем условиям Теоремы Коши на 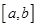 . Применим Теорему Лагранжа к функциям
. Применим Теорему Лагранжа к функциям 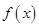 и
и 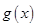 , тогда получим
, тогда получим 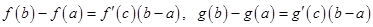 . Из последних двух равенств получим:
. Из последних двух равенств получим:
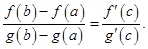 (Формула Коши)
(Формула Коши)
Найти ошибку в доказательстве.
Теоремы Лопиталя-Бернулли
Раскрытие неопределённостей типа 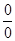 и
и 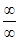
Первая теорема Лопиталя-Бернулли. Пусть для функций 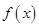 и
и 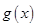 выполнены условия:
выполнены условия:
1) Функции 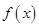 и
и 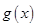 дифференцируемы в промежутке
дифференцируемы в промежутке 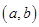 и
и 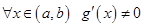
2) 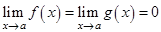
3) Существует предел 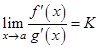 . Тогда
. Тогда 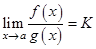
Вторая теорема Лопиталя-Бернулли. Пусть для функций 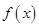 и
и 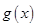 выполнены условия:
выполнены условия:
1) Функции 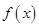 и
и 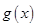 дифференцируемы в промежутке
дифференцируемы в промежутке 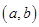 , причем
, причем 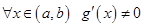
2) 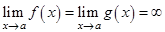
3) Существует предел 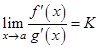 . Тогда
. Тогда 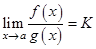
Замечание. Теоремы Лопиталя-Бернулли справедливы и при 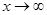 .
.
Пример 1. Вычислить предел 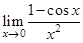 .
.
Решение.
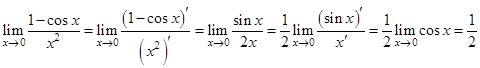
Пример 2. Вычислить предел 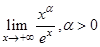 .
.
Решение.
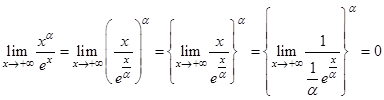
Этот пример показывает, что степенная функция 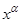 даже с очень большим показателем при
даже с очень большим показателем при 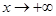 растет медленнее, чем показательная функция.
растет медленнее, чем показательная функция.
Раскрытие неопределённостей типа 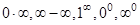
Неопределённость типа 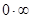 возникает при нахождении пределов от произведения двух функций, т.е.
возникает при нахождении пределов от произведения двух функций, т.е. 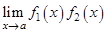 , где
, где 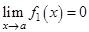 , а
, а 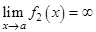 . В этом случае произведение
. В этом случае произведение 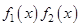 записывают так, чтобы можно было воспользоваться первой или второй теоремой Лопиталя-Бернулли.
записывают так, чтобы можно было воспользоваться первой или второй теоремой Лопиталя-Бернулли.
Пример 3. Вычислить предел 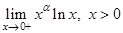 .
.
Решение. В данном примере неопределённость 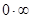 , которую сведём к неопределённости
, которую сведём к неопределённости 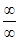 и применим вторую теорему Лопиталя-Бернулли.
и применим вторую теорему Лопиталя-Бернулли.
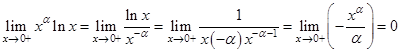 .
.
Пример 4. Вычислить предел 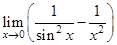 .
.
Решение. Имеем неопределённость 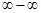 .
.
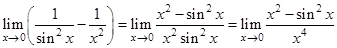 .
.
Мы воспользовались соотношением 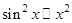 при
при 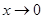 . Применяя далее первую теорему Лопиталя-Бернулли, получим:
. Применяя далее первую теорему Лопиталя-Бернулли, получим:
Неопределённости вида 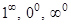 возникают при вычислении пределов
возникают при вычислении пределов 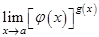 . Для вычисления данного предела предварительно вычисляют предел
. Для вычисления данного предела предварительно вычисляют предел 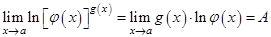 . Отсюда следует, что
. Отсюда следует, что 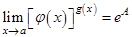 .
.
Таким образом, раскрытие неопределенностей 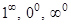 сводится к раскрытию соответственно неопределённостей
сводится к раскрытию соответственно неопределённостей 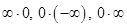 , которые в свою очередь могут быть сведены к раскрытию неопределённостей
, которые в свою очередь могут быть сведены к раскрытию неопределённостей 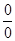 или
или 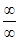 с применением соответствующих теорем Лопиталя-Бернулли.
с применением соответствующих теорем Лопиталя-Бернулли.
Пример 5. Вычислить предел 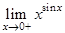 .
.
Решение. Имеем неопределённость 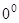 . Предварительно вычислим предел
. Предварительно вычислим предел 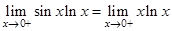 . В данном случае мы использовали соотношение
. В данном случае мы использовали соотношение 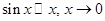 , и результат примера 3.
, и результат примера 3.
Пример 6. Вычислить предел 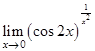 .
.
Решение. Имеем неопределённость 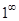 . Логарифмируя и применяя теорему Лопиталя-Бернулли, получим:
. Логарифмируя и применяя теорему Лопиталя-Бернулли, получим:
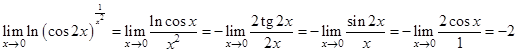 .
.
Отсюда имеем: 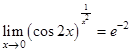 .
.
Найти следующие пределы
6. 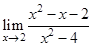 | 14. 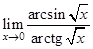 | 22. 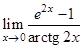 |
7. 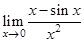 | 15. 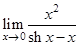 | 23. 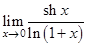 |
8. 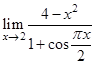 | 16. 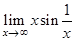 | 24. 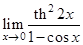 |
9. 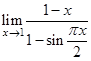 | 17. 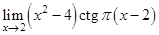 | 25. 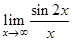 |
10. 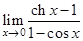 | 18. 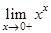 | 26. 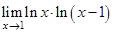 |
11. 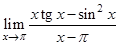 | 19. 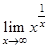 | 27. 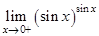 |
12. 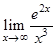 | 20. 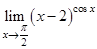 | 28. 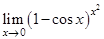 |
13. 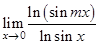 | 21. 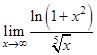 | 29. 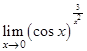 |
Формула Тейлора
Если функция 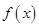 в некоторой окрестности точки
в некоторой окрестности точки 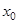 имеет
имеет 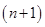 производную, то для любого
производную, то для любого 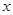 из этой окрестности справедлива формула Тейлора
из этой окрестности справедлива формула Тейлора
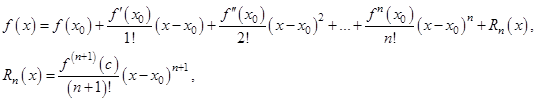
или
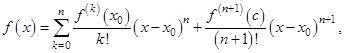
где 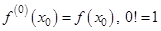 (по определению). Точка
(по определению). Точка 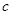 расположена между
расположена между 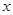 и
и 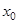 . В данном случае остаточный член записан в форме Лагранжа.
. В данном случае остаточный член записан в форме Лагранжа.
Полагая в формуле Тейлора 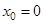 , получим формулу Маклорена.
, получим формулу Маклорена.
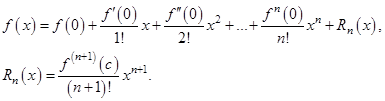
Пример 7. Многочлен 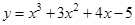 разложить по степеням
разложить по степеням 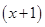 .
.
Решение. Так как данный многочлен имеет степень 3, то все производные порядка выше 3 будут тождественно равны нулю. В данном случае 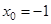 .
.
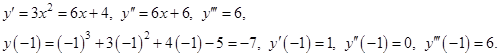
По формуле Тейлора имеем:
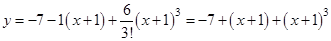 .
.
Написать формулу Маклорена при 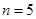 для функций
для функций
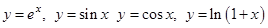
Написать формулу Тейлора при 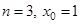 для функций
для функций
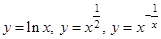 .
.
Формула Тейлора (в частности Маклорена) часто используется в приближённых вычислениях.
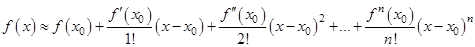 или
или
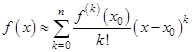 .
.
При этом ошибка равна 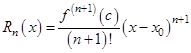 , где точка
, где точка 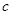 расположена между
расположена между 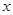 и
и 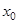 .
.
Пример 8. Вычислить 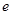 с точностью
с точностью 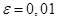 .
.
Решение. Рассмотрим функцию 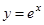 , которая бесконечное число раз дифференцируема на всей числовой оси, при этом
, которая бесконечное число раз дифференцируема на всей числовой оси, при этом 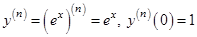 . Поэтому для функции
. Поэтому для функции 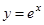 можно написать формулу Маклорена при любом
можно написать формулу Маклорена при любом 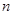 .
.
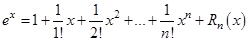 ,
,
где 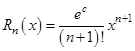 , точка
, точка 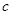 расположена между 0 и
расположена между 0 и 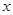 .
.
При 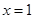 будем иметь:
будем иметь:
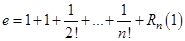 , где
, где 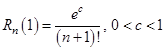
Отсюда имеем:
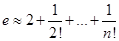 , при этом ошибка равна
, при этом ошибка равна 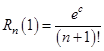 .
.
Оценим остаток, учитывая неравенство 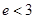 ,
, 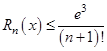 . Подберём наименьшее
. Подберём наименьшее 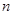 , чтобы выполнялось неравенство
, чтобы выполнялось неравенство 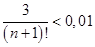 . Легко видеть, что
. Легко видеть, что 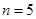 , т.к.
, т.к. 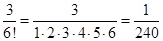 . Следовательно,
. Следовательно, 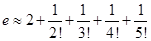 .
.
Вычислить с точностью до 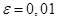 следующие значения
следующие значения
30. а) 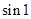 б)
б) 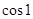 в)
в) 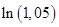 г)
г) 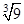
Исследование функций и построение графиков
