Асимптоты. Исследование функций и построение графиков

1. Прямая L является асимптотой графика функции у=f(x), если расстояние от точки (х,f(х)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.Асимптоты бывают вертикальными, горизонтальными и наклонными.

2. Прямая х=х₀ является вертикальной асимптотой графика функции у=f(x), если хотя бы один из пределов lim f (x) (правосторонний или левосторонний) равен ±∞. x→x₀±0

3. Прямая y=b является горизонтальной асимптотой, если lim f(x)=b

x→∞

Если lim f(x)=b , то y=b-правосторонняя асимптота,

x→+∞

если lim f(x)=b , то y=b-левостороняя асимптота.

x→-∞

4. Общая схема исследования функций и построения графиков.

1. Найти область определения функции

2. Исследовать функцию на четность-нечетность

3. Найти вертикальные асимптоты

4. Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты

5. Найти экстремумы и интервалы монотонности функции

6. Найти интервалы выпуклости функции и точки перегиба

7. Найти точки пересечения графика функции с осями координат.

8. Построить график функции.

Применение производной в задачах с экономическим содержанием

Функция издержек С(х) определяет затраты, необходимые для производства х единиц данного продукта.

Прибыль Р(х) = D(x) –C(x),где D(x)-доход от производства х единиц продукта.

Средние издержки А(х) при производстве х единиц продукта есть С(х)/х.Предельные издержки М(х)=С'(х).

Оптимальным значением выпуска для производителя является то значение х единиц продукта, при котором прибыль Р(х) оказывается наибольшей.

Семинар№8.

ПЗ 7-8. Приложение производной. Функции нескольких переменных.

1. Разбор домашнего задания №7

2. 1) Найти интервалы монотонности и точки эксремума функции 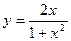. Вычислить наибольшее и наименьшее значения этой функции на отрезке .

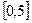2) Найти интервалы монотонности и точки эксремума функции 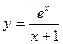. Вычислить наибольшее и наименьшее значения этой функции на отрезке .

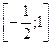3) Написать уравнение касательной к кривой 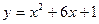в точке с абсциссой .

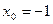4) Написать уравнение касательной к кривой 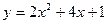в точке с абсциссой .

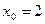Дифференциал функции.

1. Приращение ∆у дифференцируемой функции у=f(x) может быть представлено в виде:

∆у= f'(x) ∆x + a (∆x) ∆x, где ∆x- приращение независимой переменной.

2. Дифференциалом функции у=f(x) называется главная, линейная относительно ∆x часть приращения функции, равная произведению производной на приращение независимой переменной:

Dy= f'(x) ∆x/

Дифференциал независимой переменной равен приращению этой переменной: dx=∆x/

Свойства дифференциала:

1. dc=0, c- const.

2. d(u±v)=du±dv.

3. d(u/v)=vdu-udv/v².

4. d(cu)=c du.

5. d(uv)=v du + u dv.

6. dy=f'(u)du.

Семинар№9. Методы интегрирования неопределенного интеграла.