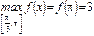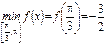Наибольшее и наименьшее значения функции
(§5,п.25)
Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции. Для случая, когда функция 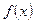 не только непрерывна на отрезке
не только непрерывна на отрезке 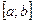 , но имеет на этом отрезке лишь конечное число критических точек, существует правило отыскания наибольшего и наименьшего значений функции f :
, но имеет на этом отрезке лишь конечное число критических точек, существует правило отыскания наибольшего и наименьшего значений функции f :
Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.

Пример 1.Найти наибольшее и наименьшее значения функции
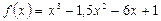 на отрезке
на отрезке 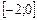 .
.
Решение:
Для нахождения наибольшего и наименьшего значений функции, согласно правилу, необходимо найти критические точки заданной функции и выделить из них те, которые принадлежат отрезку 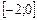 .
.
Найдем критические точки, то есть точки, в которых производная не существует или равна нулю.
Так как производная

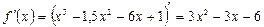
определена для любого х, то остается решить уравнение 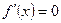 :
:
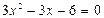 или
или 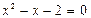 ,
,
решая полученное квадратное уравнение, получим критические точки:
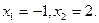
Так как критическая точка 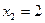 не принадлежит заданному отрезку
не принадлежит заданному отрезку 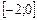 , то для нахождения наибольшего и наименьшего значений функции нужно найти значения функции на концах отрезка, то есть в точках
, то для нахождения наибольшего и наименьшего значений функции нужно найти значения функции на концах отрезка, то есть в точках 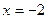 и
и 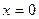 и в критической точке
и в критической точке 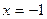 .
.
Найдем эти значения:
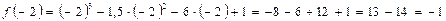
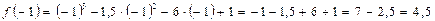
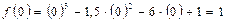 .
.
Из полученных значений выберем набольшее и наименьшее. Таким образом, наибольшее значение для заданной функции достигается в точке 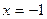 и равно 4,5 , а наименьшее – в точке
и равно 4,5 , а наименьшее – в точке 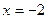 и равно –1.
и равно –1.
Ответ: 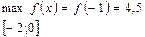 ;
; 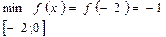
Пример 2 Представьте число 3 в виде суммы двух положительных слагаемых так, чтобы сумма их четвертых степеней была наименьшей.
Решение:
Обозначим искомые слагаемые через х и у, тогда число 3 можно представить в виде:
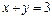 , (*)
, (*)
причем 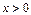 ,
, 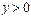 .
.
По условию задачи сумма 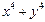 должна быть наименьшей. Представим эту сумму в виде функции:
должна быть наименьшей. Представим эту сумму в виде функции:
 (**)
(**)
Выразив переменную у через х из уравнения (*) и подставив ее значение в выражение (**), получим функцию, зависящую от переменной х :
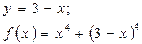 . (***)
. (***)
Исследуем данную функцию на экстремумы. Для этого определим производную:
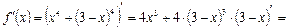
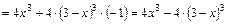 .
.
Найдем критические точки функции, для чего решим уравнение:
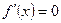 ,
,
учитывая значение производной, получим:
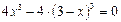 .
.
Сократив все уравнение на 4 и используя формулу разности кубов 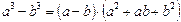 ,получим:
,получим:
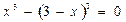
или 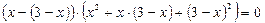 .
.
Выполняя действия внутри скобок, применяя формулу  , имеем:
, имеем:
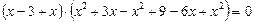
или 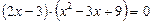 .
.
Это уравнение равносильно совокупности двух уравнений:
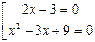 .
.
Второе из данных уравнений не имеет решений, так как его дискриминант меньше нуля, а решением первого уравнения является
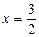 .
.
Определим знаки производной исследуемой функции слева и справа от данной точки:
 |
- +

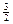 х
х
Следовательно, точка 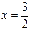 является точкой минимума функции
является точкой минимума функции 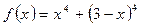 , и в этой точке данная функция принимает наименьшее значение.
, и в этой точке данная функция принимает наименьшее значение.
Таким образом, 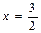 является первым слагаемым в разложении числа 3. Определим второе слагаемое, так как
является первым слагаемым в разложении числа 3. Определим второе слагаемое, так как
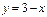 , то
, то
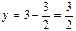 .
.
Следовательно, число 3 можно представить как сумму чисел 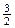 и
и 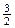 , причем сумма четвертых степеней данных слагаемых будет наименьшей.
, причем сумма четвертых степеней данных слагаемых будет наименьшей.
Ответ: 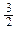 +
+ 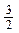 .
.
Пример 3.Найти наименьшее и наибольшее значения функции
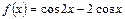 на промежутке
на промежутке 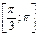 .
.
Решение:
Для нахождения наименьшего и наибольшего значений функции определим ее критические точки.
Вычислим производную заданной функции:
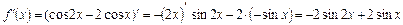
Для нахождения критических точек необходимо решить уравнение 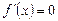 или
или
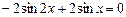
Разложим синус двойного аргумента по формуле 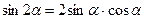 , получим:
, получим:
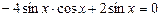
Вынесем общий множитель за скобку:
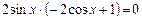 .
.
Данное уравнение равносильно совокупности уравнений:
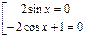 ,
, 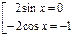 или
или 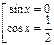 .
.
Решая каждое из полученных простейших тригонометрических уравнений, получим:
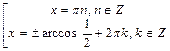 ,
, 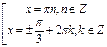 .
.
Чтобы выделить критические точки, принадлежащие заданному промежутку 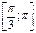 , необходимо решить неравенство
, необходимо решить неравенство 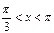 .
.
Данное неравенство равносильно совокупности неравенств:
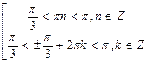 ,
,
решая данные неравенства определим значения целых чисел n и k , при которых критические точки попадают в заданный интервал 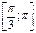 .
.
Рассмотрим решение каждого неравенства:
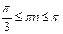 | 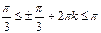 | ||
Разделим неравенство на p, получим: 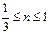 Так как n может принимать только целые значения, заключенные в промежутке Так как n может принимать только целые значения, заключенные в промежутке 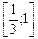 , то n = 0 или n = 1 , то n = 0 или n = 1 | Разделим неравенство на p, получим: 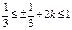 Из полученного неравенства выразим 2k: Из полученного неравенства выразим 2k: 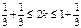 или или 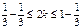 Приводя подобные члены, получим: Приводя подобные члены, получим: 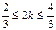 или или 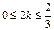 . Разделим оба неравенства на 2: . Разделим оба неравенства на 2: 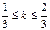 или или 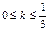 . Так как число k может принимать только целые значения из полученных промежутков, то первое неравенство решений не имеет, а во втором k = 0. . Так как число k может принимать только целые значения из полученных промежутков, то первое неравенство решений не имеет, а во втором k = 0. |

Определим критические точки при полученных значениях для n и k:
при n = 0 х = 0;
при n = 1 х = p ;
при k = 0 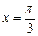 .
.
Для нахождения наименьшего и наибольшего значений функции необходимо найти значения исходной функции на концах заданного промежутка и в каждой из вычисленных критических точек. Учитывая, что критические точки 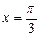 и х = p совпадают с границами заданного промежутка, то для решения исходной задачи достаточно найти значения функции в точках х = 0,
и х = p совпадают с границами заданного промежутка, то для решения исходной задачи достаточно найти значения функции в точках х = 0, 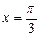 и х = p .
и х = p .
Найдем эти значения:
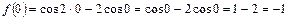 ;
;
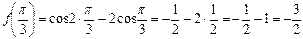 ;
;
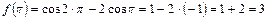 .
.
Из полученных значений нужно выбрать наибольшее и наименьшее. Наибольшее значение функции достигается в точке p и равно 3, а наименьшее – в точке 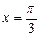 и равно
и равно 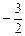 .
.
Ответ: