Наибольшее и наименьшее значения функции.

Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке множества функция не имеет большего (меньшего) значения. Н. и н. з. ф. по сравнению с её значениями во всех достаточно близких точках называются экстремумами (соответственно максимумами и минимумами) функции. Н. и н. з. ф., заданной на отрезке, могут достигаться либо в точках, где производная равна нулю, либо в точках, где она не существует, либо на концах отрезка. Непрерывная функция, заданная на отрезке, обязательно достигает на нём наибольшего и наименьшего значений; если же непрерывную функцию рассматривать на интервале (т. е. отрезке с исключенными концами), то среди её значений на этом интервале может не оказаться наибольшего или наименьшего. Например, функция у = x, заданная на отрезке [0; 1], достигает наибольшего и наименьшего значений соответственно при x = 1 и x = 0 (т. е. на концах отрезка); если же рассматривать эту функцию на интервале (0; 1), то среди её значений на этом интервале нет ни наибольшего, ни наименьшего, так как для каждого x₀ всегда найдётся точка этого интервала, лежащая правее (левее) x₀, и такая, что значение функции в этой точке будет больше (соответственно меньше), чем в точке x₀. Аналогичные утверждения справедливы для функций многих переменных.

Метод Лагранжа.

Пусть дана квадратичная форма

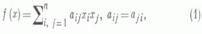
от ппеременных х ₀, x₁,..., х _п. с коэффициентами из поля k характеристики 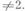Требуется привести эту форму к канонич. виду

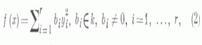
при помощи невырожденного линейного преобразования переменных. Л. м. состоит в следующем. Можно считать, что не все коэффициенты формы (1) равны нулю. Поэтому возможны два случая.

1) При некотором g, 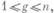диагональный коэффициент 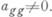Тогда

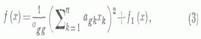
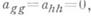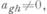где форма f₁ (х).не содержит переменную x_g.2) Если же все но то

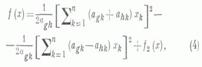
где форма f₂ (х).не содержит двух переменных x_g и x_h. Формы, стоящие под знаками квадратов в (4), линейно независимы. Применением преобразований вида (3) и (4) форма (1) после конечного числа шагов приводится к сумме квадратов линейно независимых линейных форм. С помощью частных производных формулы (3) и (4) можно записать в виде

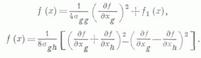
метод решения задач на Условный экстремум; Л. м. м. заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.

Для задачи об экстремуме функции f (х₁, x₂,..., x_n) при условиях (уравнениях связи) φ_i(x₁, x₂, ..., x_n) = 0, i = 1, 2,..., m, функция Лагранжа имеет вид

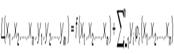
Множители y₁, y₂, ..., ym наз. множителями Лагранжа.

Если величины x₁, x₂, ..., x_n, y₁, y₂, ..., ym суть решения уравнений, определяющих стационарные точки функции Лагранжа, а именно, для дифференцируемых функций являются решениями системы уравнений

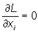i = 1, …, n; 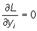i = 1, …,m,

то при достаточно общих предположениях x₁, x₂, ..., x_n доставляют экстремум функции f. Функция Лагранжа L применяется также при исследовании задач вариационного исчисления и математического программирования. Впервые Л. м. м. был предложен в 1797 Ж. Лагранжем в связи с задачами дифференциального исчисления.