Определение вариационных рядов

Различные выборочные значения назовемвариантами ряда значений и обозначим: х₁, х₂, …. Прежде всего произведем ранжирование вариантов, т.е. расположение их в порядке возрастания или убывания. Для каждого варианта указывается свой вес, т.е. число, которое характеризует вклад данного варианта в общую совокупность. В качестве весов выступают частоты или частости.

Частотой n_iварианта х_i называется число, показывающее сколько раз встречается данный вариант в рассматриваемой выборочной совокупности.

Частостью или относительной частотой w_iварианта х_i называется число, равное отношению частоты варианта к сумме частот всех вариантов. Частость показывает, какая часть единиц выборочной совокупности имеет данный вариант.

Последовательность вариантов с соответствующими им весами (частотами или частостями), записанная в порядке возрастания (или убывания), называется вариационным рядом.

Вариационные ряды бывают дискретными и интервальными.

Для дискретного вариационного ряда задаются точечные значения признака, для интервального – значения признака задаются в виде интервалов. Вариационные ряды могут показывать распределение частот или относительных частот (частостей), в зависимости от того, какая величина указывается для каждого варианта – частота или частость.

Дискретный вариационный ряд распределения частот имеет вид:

Варианты хi	x1	x2	…	xm
Частоты ni	n1	n2	…	nm

Сумма всех частот равна общему числу наблюдений, т.е. объему всей совокупности: n = n₁+ n₂ + … + n_m.

Дискретный вариационный ряд распределения относительных частот (частостей) имеет вид:

Варианты хi	x1	x2	…	xm
Частости wi	w1	w2	…	wm

Частости находятся по формуле 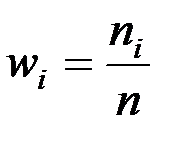, i = 1, 2, …, m.

Сумма всех частостей равна единице: w₁+ w₂ + … + w_m = 1.

Пример 4.1. Для данной совокупности чисел

4, 6, 6, 3, 4, 9, 6, 4, 6, 6

построить дискретные вариационные ряды распределения частот и частостей.

Решение. Объем совокупности равен n = 10. Дискретный ряд распределения частот имеет вид

Варианты хi
Частоты ni

Дискретный ряд распределения частостей имеет вид

Варианты хi
Частости wi	0,1	0,3	0,5	0,1

■.

Аналогичную форму записи имеют интервальные ряды.

Интервальный вариационный ряд распределения частот записывается в виде:

Интервалы	а1 – а2	а2 – а3	…	am − am+1
Частоты интервалов	n1	n2	…	nm

Сумма всех частот равна общему числу наблюдений, т.е. объему совокупности: n = n₁+ n₂ + … + n_m.

Интервальный вариационный ряд распределения относительных частот (частостей)имеет вид:

Интервалы	а1 – а2	а2 – а3	…	am − am+1
Частости интервалов	w1	w2	…	wm

Частость находится по формуле 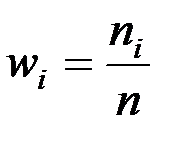, i = 1, 2, …, m.

Сумма всех частостей равна единице: w₁+ w₂ + … + w_m = 1.

Наиболее часто на практике применяются интервальные ряды. Если статистических выборочных данных очень много и их значения отличаются друг от друга на сколь угодно малую величину, то дискретный ряд для этих данных будет достаточно громоздким и неудобным для дальнейшего исследования. В этом случае применяют группировку данных, т.е. промежуток, содержащий все значения признака, разбивают на несколько частичных интервалов и, подсчитав частоту для каждого интервала, получают интервальный ряд. Запишем более подробно схему построения интервального ряда, предположив, что длины частичных интервалов будут одинаковыми.

2.2 Построение интервального ряда

Для построения интервального ряда нужно:

- определить число интервалов;

- определить длину интервалов;

- определить расположение интервалов на оси.

Для определения числа интервалов k существует формула Стерджеса, по которой

,

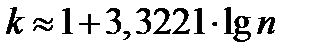где n - объем всей совокупности.

Например, если имеется 100 значений признака (вариант), то рекомендуется для построения интервального ряда взять число интервалов равным 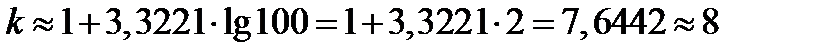интервалам.

Однако очень часто на практике число интервалов выбирает сам исследователь, учитывая, что это число не должно быть очень большим, чтобы ряд не был громоздким, но и не очень маленьким, чтобы не потерять некоторых свойств распределения.

Длина интервала h определяется по следующей формуле:

,

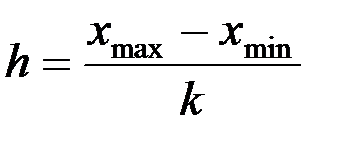где x_max и x_min - это соответственно самое большое и самое маленькое значения вариантов.

Величину называют размахом ряда.

Для построения самих интервалов поступают по-разному. Один из самых простых способов заключается в следующем. За начало первого интервала принимают величину 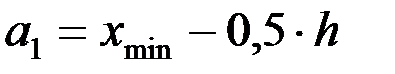. Тогда остальные границы интервалов находятся по формуле 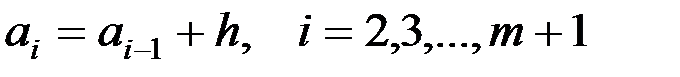. Очевидно, что конец последнего интервала a_m+1 должен удовлетворять условию

.

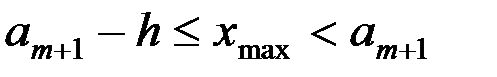После того как найдены все границы интервалов, определяют частоты (или частости) этих интервалов. Для решения этой задачи просматривают все варианты и определяют число вариант, попавших в тот или иной интервал. Полное построение интервального ряда рассмотрим на примере.

Пример 4.2. Для следующих статистических данных, записанных в порядке возрастания, построить интервальный ряд с числом интервалов, равным 5:

11, 12, 12, 14, 14, 15, 21, 21, 22, 23, 25, 38, 38, 39, 42, 42, 44, 45, 50, 50, 55, 56, 58, 60, 62, 63, 65, 68, 68, 68, 70, 75, 78, 78, 78, 78, 80, 80, 86, 88, 90, 91, 91, 91, 91, 91, 93, 93, 95, 96.

Решение. Всего n=50 значений вариантов.

Число интервалов задано в условии задачи, т.е. k=5.

Длина интервалов равна .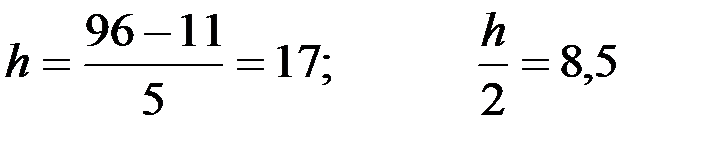

Определим границы интервалов:

a₁ = 11 − 8,5 = 2,5; a₂ = 2,5 + 17 = 19,5; a₃ = 19,5 + 17 = 36,5;

a₄ = 36,5 + 17 = 53,5; a₅ = 53,5 + 17 = 70,5; a₆ = 70,5 + 17 = 87,5;

a₇ = 87,5 +17 = 104,5.

Для определения частоты интервалов посчитываем число вариантов, попавших в данный интервал. Например, в первый интервал от 2,5 до 19,5 попадают варианты 11, 12, 12, 14, 14, 15. Их число равно 6, следовательно, частота первого интервала равна n₁=6. Частость первого интервала равна 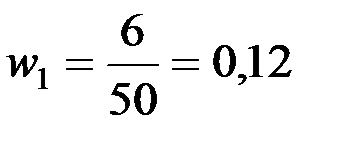. Во второй интервал от 19,5 до 36,5 попадают варианты 21, 21, 22, 23, 25, число которых равно 5. Следовательно, частота второго интервала равна n₂ =5, а частость 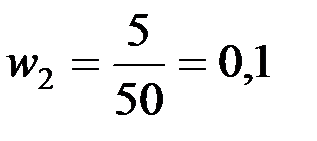. Найдя аналогичным образом частоты и частости для всех интервалов, получим следующие интервальные ряды.

Интервальный ряд распределения частот имеет вид:

Интервалы	2,5-19,5	19,5-36,5	36,5-53,5	53,5-70,5	70,5-87,5	87,5-104,5
Частоты

Сумма частот равна 6+5+9+11+8+11=50.

Интервальный ряд распределения частостей имеет вид:

Интервалы	2,5-19,5	19,5-36,5	36,5-53,5	53,5-70,5	70,5-87,5	87,5-104,5
Частости	0,12	0,1	0,18	0,22	0,16	0,22

Сумма частостей равна 0,12+0,1+0,18+0,22+0,16+0,22=1. ■

При построении интервальных рядов, в зависимости от конкретных условий рассматриваемой задачи, могут применяться и другие правила, а именно

1. Интервальные вариационные ряды могут состоять из частичных интервалов разной длины. Неравные длины интервалов позволяют выделить свойства статистической совокупности с неравномерным распределением признака. Например, если границы интервалов определяют численность жителей в городах, то целесообразно в данной задаче использовать неравные по длине интервалы. Очевидно, что для небольших городов имеет значение и небольшая разница в числе жителей, а для больших городов разница в десятки и сотни жителей не имеет существенного значения. Интервальные ряды с неравными длинами частичных интервалов исследуются, в основном, в общей теории статистики и их рассмотрение выходит за рамки данного пособия.

2. В математической статистике иногда рассматривают интервальные ряды, для которых левую границу первого интервала полагают равной –∞, а правую границу последнего интервала +∞. Это делается для того, чтобы приблизить статистическое распределение к теоретическому.

3. При построении интервальных рядов может оказаться, что значение какого-то варианта совпадает в точности с границей интервала. Лучше всего в этом случае поступить следующим образом. Если такое совпадение только одно, то считать, что рассматриваемый вариант со своей частотой попал в интервал, находящийся ближе к середине интервального ряда, если таких вариантов несколько, то либо все их отнести к правым от этих вариант интервалам, либо все – к левым.

4. После определения числа интервалов и их длины, расположение интервалов можно производить и по другому способу. Находят среднее арифметическое всех рассматриваемых значений вариантов х_ср. и строят первый интервал таким образом, чтобы это среднее выборочное находилось бы внутри какого-то интервала. Таким образом, получаем интервал от х_ср.– 0,5h до х_ср..+ 0,5h. Затем влево и вправо, прибавляя длину интервала, строим остальные интервалы до тех пор, пока x_min и x_max не попадут соответственно в первый и последний интервалы.

5. Интервальные ряды при большом числе интервалов удобно записывать вертикально, т.е. интервалы записывать не в первой строке, а в первом столбце, а частоты (или частости) во втором столбце.

Выборочные данные могут рассматриваться как значения некоторой случайной величины Х. Случайная величина имеет свой закон распределения. Из теории вероятностей известно, что закон распределения дискретной случайной величины можно задать в виде ряда распределения, а непрерывной – с помощью функции плотности распределения. Однако существует универсальный закон распределения, который имеет место и для дискретной и для непрерывной случайных величин. Этот закон распределения задается в виде функции распределения F(x) = P(X<x). Для выборочных данных можно указать аналог функции распределения – эмпирическую функцию распределения.