Исследование функции и построение графиков

При исследовании функций и построения их графиков рекомендуется использовать следующую схему.

1. Найти область определения функции.

2. Найти точки пересечения с осями координат, если они существуют. Найти интервалы знакопостоянства функции.

3. Проверить, является ли функция четной, нечетной, периодической. График четной функции симметричен относительно оси ОУ. График нечетной функции симметричен относительно начала координат.

4. Исследовать функцию на непрерывность. Найти точки разрыва и односторонние пределы в точках разрыва. Определить характер разрыва в окрестности точек разрыва. Найти вертикальные, горизонтальные, наклонные асимптоты графика, если они существуют.

5. С помощью производной первого порядка найти промежутки возрастания и убывания, найти экстремумы.

6. С помощью производной второго порядка найти промежутки выпуклости и вогнутости, точки перегиба.

7. Используя полученную информацию, построить график.

Пример 1. Исследовать функцию и построить ее график.

Решение: Область определения .

Функция не является ни четной, ни нечетной, т.к. . Функция не периодическая.

Нули функции: .

Отметим интервалы знакопостоянства функции на числовой оси. На оси обязательно надо нанести точку 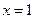, в которой функция не определена. Знак функции 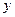зависит от знака числителя , т.к. знаменатель при всех :

- + + +

.

Выясним тип разрыва в точке 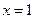. Для этого найдем пределы функции слева и справа в этой точке.

, . Значит, точка 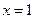- есть точка разрыва второго рода. Прямая 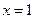- вертикальная асимптота графика функции.

Найдем наклонные асимптоты:

,

.

Прямая - наклонная асимптота.

Найдем производную функции:

.

Найдем критические точки первого рода – точки, в которых первая производная равна нулю или не существует:

при , т.е. ;

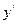не существует в точке .

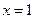Исследуем знак 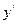в окрестностях этих точек:

+ + - +

.

Функция возрастает на промежутках ;

Функция убывает на интервале .

Точка - есть точка минимума функции, точка 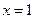не является точкой экстремума, т.к. функция в этой точке не определена.

Найдем вторую производную функции:

.

Найдем критические точки второго рода:

при , т.е. ;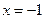

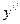не существует в точке .

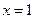Исследуем знак 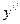в окрестностях точек .

- + +

.

Точка 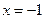- есть точка перегиба.

На интервале график функции выпуклый.

На промежутке график функции вогнутый.

Пример 2. Исследовать функцию и построить ее график.

Решение: Функция определена на всей числовой оси.

Функция общего вида, т.к. . Функция не имеет точек разрыва, значит, не имеет точек вертикальных асимптот.

Точка пересечения с осями координат одна .

Найдем наклонные асимптоты.

Вычислим .

.

Применяя правило Лопиталя .

Только для 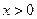функция имеет горизонтальную асимптоту .

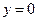Первая производная определена на всей числовой оси, т.е. крититческими точками первого рода могут быть только нули производной: , .

Исследуем знак производной в окрестности точки :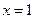

+ -

.

Функция возрастает на интервале 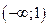; убывает на интервале 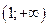. При переходе через точку 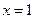производная меняет знак с плюса на минус. Значит, точка 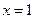является точкой максимума. .

Вторая производная определена на всей числовой оси, т.е. точки перегиба могут быть только там, где

: . На интервале , значит, график функции выпуклый; на интервале , значит, график функции вогнутый. Точка является точкой перегиба функции.

Пример 3. Исследовать функцию и построить ее график. Решение: Функции определены для любого значения 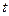. Поскольку функция 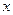четная, а функция 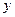нечетная, то график функции симметричен относительно оси ординат и начала координат, т.е. относительно координатных осей.

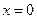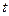Полагая , находим, что и . При таких значениях из выражения находим, что .

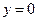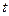Полагая , находим, что и . При этих значениях из выражения находим, что . Таким образом, график функции пересекает координатные оси в точках .

Найдем производные , , , . Из выражения для производной 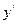определяем критические точки. При , производная равна нулю, а при , не существует. Таким образом, область изменения параметра 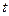разбивается на четыре интервала .

При производная , т.е. функция убывает и график функции вогнутый. При , т.е. функция возрастает и график вогнутый. При , т.е. функция убывает и график выпуклый. При , т.е. функция возрастает и график выпуклый. Пользуясь симметрией графика функции, этот анализ можно было ограничить изменением параметра только одним интервалом, например. .

При производная и касательные совпадают с осью 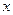, т.е. точки будут точками возврата. При производная 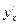не существует, а при 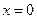, касательные совпадают с осью 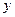и точки будут также точками возврата. Полученная кривая представляет собой траекторию движения точки подвижного круга, катящегося изнутри по неподвижному кругу радиуса 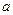, и называется астроидой.

Исследовать функции и построить их графики:

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

Варианты типового расчета

Вариант

1. Найти наибольшее и наименьшее значения функции

а отрезке

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Какие размеры должен иметь прямой круговой цилиндр, поверхность которого равна , чтобы его объем был наибольшим?

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Доказать, что из всех прямоугольников, имеющих данный периметр , наибольшую площадь имеет квадрат.

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Доказать, что из всех прямоугольников, имеющих данную площадь , квадрат имеет наименьший периметр.

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Консервная банка объемом 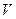должна иметь цилиндрическую форму с дном и крышкой. Каково должно быть отношение диаметра основания цилиндра к его высоте, чтобы на изготовление банки пошло наименьшее количество жести?

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. В равнобедренный треугольник с основанием 20 см и высотой 8 см вписан прямоугольник, одна из сторон которого лежит на основании треугольника. Какова должна быть высота прямоугольника, чтобы он имел наибольшую площадь?

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Полотняный шатер объемом 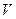имеет форму прямого кругового конуса. Каково должно быть отношение высоты конуса к радиусу основания, чтобы на шатер ушло наименьшее количество полотна.

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. В прямоугольный треугольник с гипотенузой 10 см и углом в 30 вписан прямоугольник, основание которого расположено на гипотенузе. Каковы должны быть размеры этого прямоугольника, чтобы его площадь была наибольшей?

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Требуется изготовить коническую воронку с образующей L. Какова должна быть высота воронки, чтобы вместимость ее была наименьшей?

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Определить размеры прямого открытого бассейна объемом 32 м 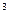с квадратным дном так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Найти высоту 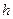прямого кругового конуса наименьшего объема, описанного около полушара радиуса так, чтобы центр основания конуса лежал в центре шара.

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Найти прямоугольный треугольник наибольшей площади, имеющий гипотенузой отрезок .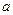

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Сопротивление балки прямоугольного поперечного сечения на сжатие пропорционально площади этого сечения. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром , чтобы ее сопротивление на сжатие было наибольшим?

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Чтобы по возможности уменьшить трение жидкости о стенки канала, площадь, стачиваемая водой, должна быть, возможно, меньшей. Показать, что лучшей формой открытого прямоугольного канала с заданной площадью поперечного сечения является такая, при которой ширина канала превышает вдвое его высоту.

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. На оси параболы дана точка на расстоянии 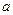от вершины. Найти абсциссу ближайшей к ней точки кривой.

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Найти высоту прямого кругового цилиндра с наибольшим объемом, который может быть вписан в шар радиуса .

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Найти высоту прямого кругового конуса с наименьшим объемом, описанного около шара радиуса .

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Какова должна быть сторона основания правильной треугольной призмы данного объема 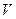, чтобы полная поверхность призмы была наименьшей?

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. На прямой, соединяющей два источника света, найти наименее освещенную точку, если силы света источников относятся как 64:27, а расстояние между ними равно 35 см.

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. В прямоугольной системе координат через точку (1;2) проведена прямая с отрицательным угловым коэффициентом, которая вместе с осями координат образует треугольник. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей?

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Стрела прогиба балки прямоугольного поперечного сечения обратно пропорциональна произведению ширины этого сечения на куб его высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром , с наименьшей стрелой прогиба (наибольшей жесткости)?

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. В прямоугольной системе координат через точку (1;4) проведена прямая, пересекающаяся с положительными полуосями координат. Написать уравнение прямой, если сумма отрезков, отсекаемых ею на осях координат, принимает наименьшее значение.

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Сопротивление балки прямоугольного поперечного сечения на изгиб пропорционально произведению ширины этого сечения на квадрат его высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром , чтобы ее сопротивление на изгиб было наибольшим?

Вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Требуется устроить площадку в форме равнобедренного треугольника так, чтобы с двух сторон она была ограничена проволочной сеткой, а третья сторона (основание треугольника) примыкала к длинной каменной стене. Найти размеры треугольника наибольшей площади, если имеется 100 погонных метров сетки.

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Требуется сделать открытый сверху желоб, поперечное сечение которого имеет форму равнобочной трапеции, а дно и бока имеют ширину по 100 см. Какова должна быть ширина желоба наверху, чтобы он вмещал наибольшее количество воды?

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Требуется изготовить цилиндрический сосуд заданного объема 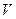, открытый сверху. Определить его радиус и высоту так, чтобы поверхность была наименьшей.

Вариант

1. Найти наибольшее и наименьшее значения функции на отрезке .

2. Провести полное исследование функций и построить их графики: a) ; b) ; с) .

3. Найти высоту прямого кругового конуса с наименьшим объемом, описанного около шара радиуса R.