Правило лопиталя, при 0 / 0

25. 26.

если α(х) ~ β(х) бесконечно малые, то α(х) - β(х) есть величина бесконечно малая более высокого порядка малости.

Если α(х) - β(х) есть величина бесконечно малая более высокого порядка малости по сравнению с α(х) и β(х) то α(х) ~ β(х).

Предел α(х) и β(х) не изменится, если каждой из этих величин или одну из них заменить эквивалентной величиной.

Если α(х) и β(х) равны поразнь γ(х), то они равносильны между собой.

Если при х→х₀ бесконечно малая функция α(х)низшего порядка малости, чем каждая из бесконечно малых β₁(х), β₂(х),…, β_n(х),то бесконечно малая γ(х)= α(х)+ β₁(х)+β₂(х)+…+β_n(х) эквивалентна бесконечно малой α(х).

27. Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке:

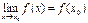
Это означает:

- функция определена в точке х₀ и в ее окрестности;

- функция имеет предел при х→х₀

- предел функции в точке х₀ равен значению функции в этой точке, т.е. выполняется равенство.

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х₀

29. Точки разрыва функции – это точки в которых нарушается непрерывность функции.

Точка разрыва х₀ называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)

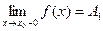и

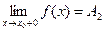
При этом, если:

- А₁=А₂ то точка х₀ называется точкой устранимого разрыва;

- А₁≠А₂ то точка х₀ называется точкой конечного разрыва.

|A₁ – A₂| называется скачком функции.

Точка разрыва х₀ называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.

30. непрерывные на отрезке функции имеют ряд важных свойств. Теорема1. Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего или наименьшего значений. Следствие: если функция непрерывна на отрезке, то она ограничено на этом отрезке. 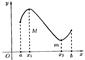Теорема2.Если функция y=f(x) непрерывна на отрезке [a, b] и принимает на его концах неравные значения f(a)=A, f(b)=B, то на этом отрезке она принимает и все промежуточные значения между А и В. Следствие: Если функция y=f(x) непрерывна на отрезке [a, b] и на его концах принимает значения разных знаков, то внутри отрезка [a, b] найдется хотя бы одна точка с, в которой данная функция обращается в 0.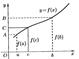

31. Производной функции y=f(x) в точке х₀ наз. предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0.

Если функция y=f(x) описывает какой-либо физический процесс, то производная y’ есть скорость протекания этого процесса. В этом состоит механический смысл производной.

Производная f’(x) в точке x равно угловому коэффициенту касательной к графику функции y=f(x) в точке, абсцисса кот. равна х. в этом заключается геометрический смысл производной.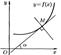

32. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.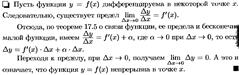

33.Теорема: Если f(x) и g(x) дифферен. в точке х, то: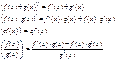

Теорема о произв. сложной функции:

Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).

Теорема о произв. обратной функции.

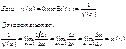
Таблица производных:

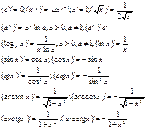
34.степенная функция y=xⁿ ,n€N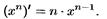

Показательная y=a^x, a>0, a≠1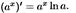

Логарифмическая y=log_ax , a>0, a≠1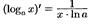

Тригонометрические y=cosx, y=sinx, y=tgx, y=ctgx 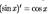(cosx)’=-sinx (tgx)’= (ctgx)’=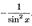

Обратные тригонометрические y=arccosx, y=arcsinx, y=arctgx, y=arcctgx :(arccosx)’= 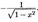(arcsinx)’= 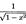(arctgx)’= 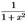(arcctgx)’= -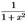

35. 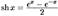гиперболический синус. 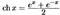гиперболический косинус. 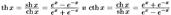гиперболический тангенс и котангенс.

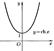
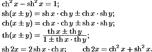
36. для вычисления производных необходимо знать лишь правила дифференцирования и формулы производных основных элементарных функций.

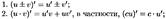
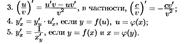
37. Неявной называется такая ф-ция у аргумента х, если она задана уравнением F(x,y)=0, не разрешенным относительно независимой переменной.

y=f(x), y=x²-1 - явные

F(x,y)=0, a²=x²+y² - неявные ф-ции.

1)a²=x²+y² - найдем производную, продифференцируем, считая у - сложной ф-цией х.

y`=2x+2y=0, т.к. а- постоянная

y*y`=-x, y`=-x/y

2) x³-3xy+y³=0

3x³-3(xy)`+3y<sup>2</sup>*y`=0 //:3

x²-(x`y+y`x)+y²*y`=0

y`y<sup>2</sup>-xy`=y-x²

y`=(y-x²)/(y²-x)

38. {x=ϕ(t), y=ᴪ(t), t€T}

ϕ'(t), ᴪ’(t) – существует.! ϕ'(t)≠0

y_x’=y_t’\x_t’

формула, дает возможность находить y_x’ от функций, не находя непосредственно зависимости между х и у.

39. Логарифмическое дифференцирование -в некоторых случаях целесообразнее функцию сначала прологарифмировать, а результат продифференцировать.

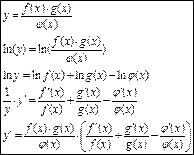
Однако производные степенных функций находят только логарифмическим дифференцированием.

Производная степенно-показательной функции равна сумме производно показательной функции, при условии U=const, и производной степенной функции, при условии V=const.

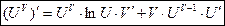
40. limy=A, y=A+a

limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx

Dx®0

Dy=y`Dx+e, где e-б.м.в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.

dy=y`Dx

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.

Если y=x, то dy=dx=x`Dx=Dx, dx=Dx

Если y¹x, то dy=y`dx, y`=dy,dx

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину Dx

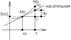
41.dy= f ′(х)* dх ; y=f(U); U=ϕ(x)

dy= f ′(U)* dU форма дифференциала не меняется как для независимого х так и для сложной функции. В этом и состоит интервариантность формы дифференциалов.

42. как известно приращение ᴧу функции y=f(x) в точке х можно представить в виде ᴧу= f ′(x)*ᴧх+α*ᴧх, где α→0 при ᴧх→0 или ᴧу= dy+ α*ᴧх. отбрасывая конечно бесконечно малую α*ᴧх более высокого порядка, чем ᴧх, получаем приближенное равенство ᴧу~ dy, причем это равенство тем точнее, чем меньше ᴧх. это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

43. пусть дана функция y=f(x), кот. имеет в нек. области производную y’=f’(x). Может оказаться, что f’(x) может иметь производную(у’)’=(f’(x))’. Эта производная по отношению к f’(x) наз. производной второго порядка. Тогда у’- производная первого порядка. Для производных 2порядка вводят обозначение d²y\dx²(d2y по dx квадрат). a) Нахождение производной от функции y=f(x) до данного порядка наз. последовательным дифференц. этой функции. S’(t)=V(t); V’(t)=a; a=S”(t). b) F(x, y)=0. дифференц. по х, считая у функцией по х.

c) {x=ϕ(t), y=ᴪ(t), t€T} y_x’=y_t’\x_t’ ; y_xx”= (y_x’)_t’\x_t’

44. Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференциал этой функции. Дифференциал от дифференциала есть второй дифференциал.

Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

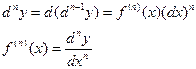Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

45. 1.Теорема Ролля.

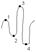Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с из интерв. (a,b), такая, что f’(c)=0.

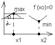
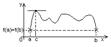
2. Теорема Лагранжа.

Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.

т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).

Доказательство: применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.

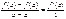
3. Теорема Коши.

Если f(x), g(x) удовл. трем условиям:

1). f(x), g(x) непрерыв. на промеж [a,b]

2). f(x), g(x) деффер. на интервале (a,b)

3). g’(x)¹0 на интер. (a,b), то сущ. т. с

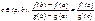
g(b)¹g(a) (неравны по теореме Ролля).

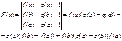
1). F(x) – непрерывна на [a,b]

2). F(x) – деффиренцирована на (a,b)

3). F(a)=0 ; F(b)=0

по теореме Ролля сущ. сÎ(a,b); F’(с)=0

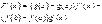
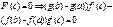
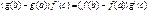
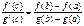
4. если функция f(x),определенная в интервале (a,b) принимает в какой-то точке с этого интервала наибольшее или наименьшее значение и имеет в этой точке производную, то эта производная =0

46.

Правило Лопиталя, при 0 / 0.