Исследование функций и построение графиков

Общее исследование функций и построение их графиков удобно выполнять по следующей схеме:

1. Найти область определения функции.

2. Найти точки пересечения с осями координат.

3. Выяснить, не является ли функция четной или нечетной, периодической или непериодической.

3.Найти точки экстремума функции, вычислить значения функции

в этих точках. Установить интервалы монотонности функции.

4. Найти точки перегиба графика функции, вычислить значения функции в этих точках. Установить интервалы выпуклости и вогнутости графика функции.

6. Найти асимптоты графика функции.

7. Используя результаты исследований, построить график функции.

Задача 4. Исследовать функцию 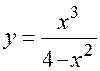и построить ее график.

Решение: 1. Функция определена и непрерывна на всей оси, кроме точек 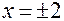, в которых функция не существует. Итак,

.

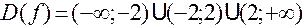2. Найдем точки пересечения с осями координат.

а) с осью ОХ: .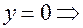

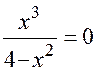
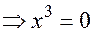
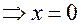Следовательно, точка пересечения с осью ОХ - ;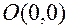

б) с осью ОY: ,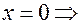

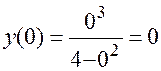следовательно, точка пересечения с осью ОY - .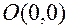

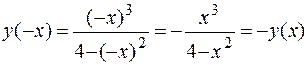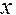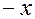3. Функция нечетная, так как (при замене на она меняет знак на противоположный, поэтому график ее будет симметричен относительно начала координат). Функция непериодическая.

4. С помощью первой производной найдем промежутки возрастания и убывания функции.

Имеем

.

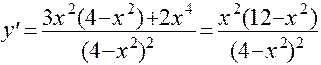Решим уравнение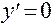 , т.е. .

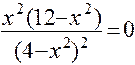Точки 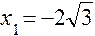, , 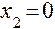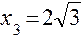будут подозрительными на экстремум. Точки 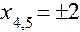, в которых производная не существует, но в этих точках не существует и функция. Разбиваем всю область определения функции на промежутки : 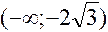, , 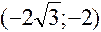, , 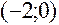, 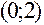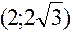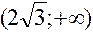и исследуем функцию для 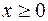. Информация о поведении функции на интервале (-2; 0) необходима для анализа функции в точке х=0.

Знак производной устанавливаем методом интервалов. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:

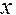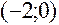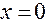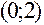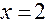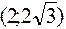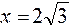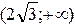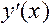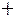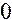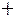				Не сущест.
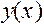	Возрас- тает	Нет экстре- мума	Возрас-тает	Не сущест.	Возрас-тает	Макс.	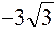Убывает

5. Чтобы исследовать функцию на выпуклость, найдем вторую производную: .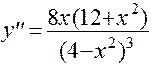

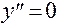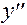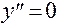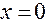Находим точки, в которых или не существуют: при и 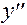не существует при 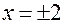. Исследуем знак второй производной на промежутках 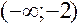, , 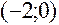, 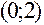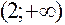и результаты исследований представим в таблице:

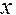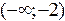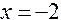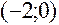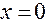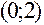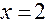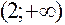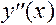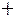		Не сущест.		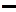		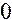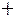Не сущест.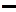
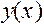	Выпук-ла	Не сущест- вует	Вогну- та	Точка переги-ба	Выпук-ла	Не Сущест- вует	Вогну-та

6. Найдем вертикальные асимптоты:

Исследуем поведение функции в окрестности точки :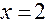

= = =+ ;

= = - .

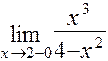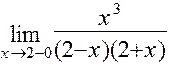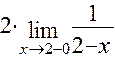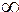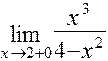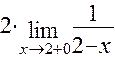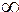Что касается точки 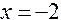, то в окрестности ее имеем:

; ;

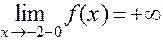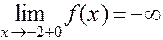Найдем наклонную асимптоту :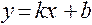

= ;

=

.

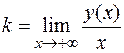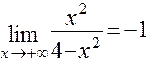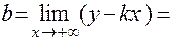
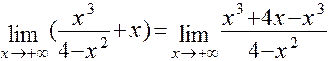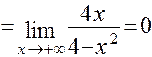Таким образом, наша функция имеет наклонную асимптоту .

Аналогично проверяется, что эта же прямая будет для нее асимптотой и при ;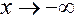

7. на основе проведенного исследования функции строим ее график (рис.1).

Рис. 1

Задача 5. Исследовать функцию 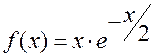и построить ее график.

Решение:

1. Область определения функции – вся числовая прямая.

2. Найдем точки пересечения графика функции с осями координат:

а) с осью OX: 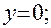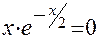; так как 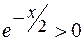, то ,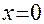

т.е. точка пересечения с осью OX – начало координат O (0,0);

б) с осью OY: при ,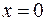

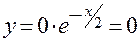т.е. точка пересечения с осью OY – начало координат O (0,0).

Используя результаты, можно определить промежутки, на которых функция сохраняет знак.

Поскольку 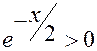, то знак функции совпадает со знаком множителя 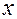. Графически промежутки знакопостоянства функции изображены на рис.2.

__ +

0

3. Определим, является ли функция четной или нечетной:

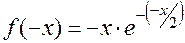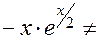
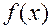= .Ясно также что

.

То есть функция не является ни четной, ни нечетной.

4. Найдем интервалы монотонности и экстремумы функции с помощью первой производной.

= .

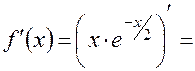
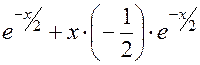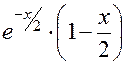Найдем возможные точки экстремума. Критические или подозрительные на экстремум точки определяются как точки, в которых 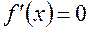или не существует:

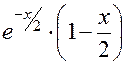=0.Так как 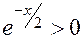при любом 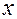, то 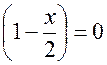.Следовательно, 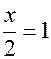или .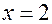

Методом интервалов находим знаки первой производной (см. рис.3) .

+ __

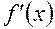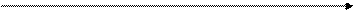
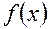
2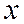

Рис. 3

Из рис. 3 видно, что 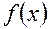возрастает для 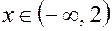, так как для этих значений 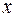выполняется неравенство 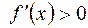и 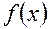убывает для 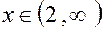, так как 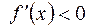при указанных значениях .

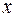При “переходе” через точку 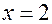функция меняет знак с “ + “ на “ __ “, следовательно, в точке 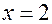функция достигает максимума.

Результаты исследования заносим в таблицу:

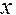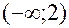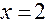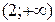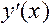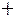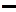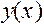	Возрастает	Макс. 0,7	Убывает

5. Определим интервалы выпуклости и вогнутости функции, а также ее точки перегиба с помощью второй производной:

.

Найдем точки, в которых вторая производная равна нулю или не существует:

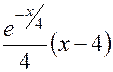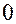= .Отсюда и, значит, .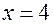

Применим метод интервалов. Находим знаки второй производной. (см. рис.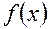4) .

__ +

4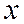

Рис.4

Из рис.4 видно, что 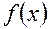вогнута для 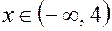, так как на этом промежутке 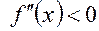и 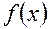выпукла для 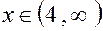, так как здесь 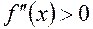. Следовательно, 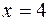является точкой перегиба функции.

Поскольку 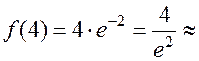0,541, то точка 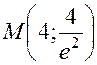является точкой перегиба графика функции .

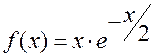Результаты исследования заносим в таблицу:

	-		+
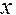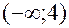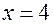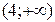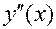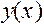	Выпукла	Перегиб	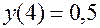Вогнута

6. Найдем асимптоты графика функции.

Так как функция непрерывна на всей числовой оси, то вертикальных асимптот нет.

Определим, имеет ли функция горизонтальные асимптоты.

Так как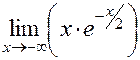 = = 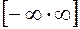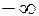,то при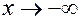горизонталь-ной асимптоты нет. Далее,

= = = .

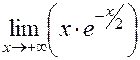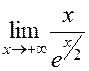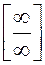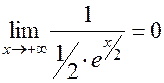Здесь мы применили правило Лопиталя.

Итак, при 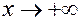функция имеет горизонтальную асимптоту: .

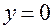Определим, имеет ли функция наклонные асимптоты,которые представляются в виде .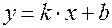

Будем искать наклонную асимптоту при :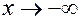

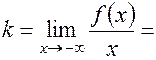
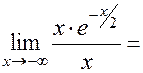
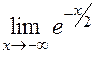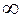= .Следовательно, при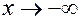наклонной асимптоты нет.

Рассмотрим теперь случай, когда 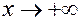.Поскольку при 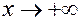функция имеет горизонтальную асимптоту, то искать наклонную асимптоту при 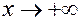не имеет смысла.

Следовательно, функция имеет только одну асимптоту – горизонтальную при .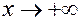

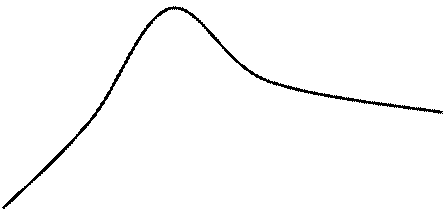
7. На основании полученных данных строим график функции (рис.5).

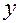
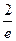
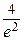
2 4

Рис.5

3. Наибольшее и наименьшее значения функций на отрезке

Задача 6. Найти наибольшее и наименьшее значения функции 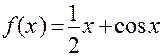на отрезке .

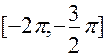Решение. Если функция 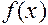непрерывна на замкнутом промежутке 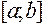, то наибольшее и наименьшее значения она принимает или на концах этого отрезка или в точках ее экстремума. Следовательно, для решения поставленной задачи надо найти ее значения на концах отрезка 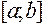и в точках, принадлежащих этому отрезку, подозрительных на экстремум. Затем из них выбрать наименьшее и наибольшее значения. Определяем критические, или стационарные, точки функции :

; ; ; , .

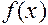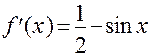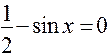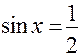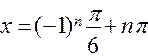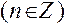Рассматриваем только те стационарные точки, которые принадлежат отрезку .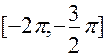

Такой точкой будет точка 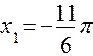(точку 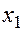получаем при ).

Вычисляя значения функции на концах промежутка и в точке 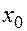, находим:

1) ;

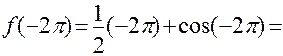
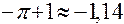2) = ;

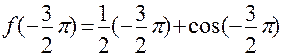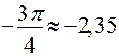3) = .

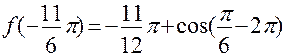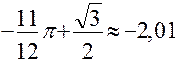Ясно, что наибольшее значение функции будет равно 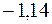, которое она принимает в точке 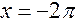; наименьшее значение принимается функцией в точке 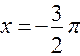и равно .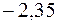