Потенциальное поле и его свойства

Векторное поле 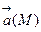называют потенциальным в области (G), если существует такая скалярная функция (скалярное поле) 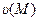, заданная в (G), что для всех точек этой области: 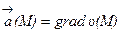. Функцию 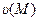называют потенциалом поля .

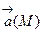В потенциальном поле линейный интеграл не зависит от формы пути и определятся только начальной и конечной точками пути, а именно

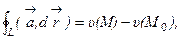
где М₀ и М – начальная и конечная точка линии (L).

Верно и обратное: если линейный интеграл поля (М) не зависит от пути, то поле (М) потенциально. Потенциал поля определяется с точностью до постоянного слагаемого. Это означает, что если 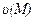один из потенциалов поля 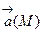, то выражения 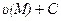при любом постоянном С также являются потенциалами поля. Задание величины потенциала в какой- либо точке М₀ области (V) однозначно определяет потенциал любой точки М:

, (*)

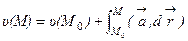где вместо 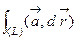использовано обозначение 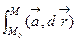, поскольку интеграл не зависит от пути.

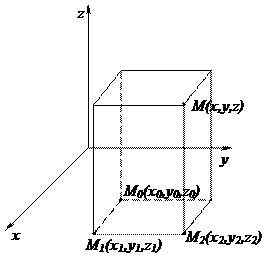Если поле задано в декартовой координатной форме: 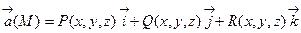, то для нахождения потенциала точки М(x,y,z) удобно взять линейный интеграл по ломанной М₀М₁М₂М_, звенья которой параллельны координатным осям.

Предполагается, конечно, что ломаная М₀М₁М₂М не выходит за пределы области (G). При таком выборе пути интегрирования и при дополнительном условии 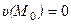выражение (*) принимает вид:

(*)

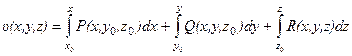При использовании этой формулы следует иметь в виду, что в каждом из трех входящих в нее интегралов одной буквой обозначают и верхний предел, и переменную интегрирования, т.е.

Рис. 5.

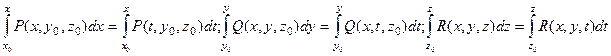
Отметим, что потенциальность поля 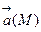и равенство нулю циркуляции поля по искомому простому кусочно-гладкому замкнутому контуру являются эквивалентными свойствами.

Если поле 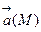потенциально в области (G), то в любой точке этой области 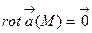. Это свойство потенциального поля является наиболее важным. Таким образом, потенциальное поле (М) является безвихревым. Обратное, вообще говоря, неверно. Однако, если ограничиться поверхностно односвязными областями, то для таких областей понятие потенциального и безвихревого полей оказываются эквивалентными.

Примеры

66. Проверить, что поле =(y+z) + (z+x) +(x+y) является потенциальным, и найти его потенциал.

Решение. Поле определено во всем пространстве, т.е. в односвязной области, поэтому достаточно проверить, что rot =0. Имеем:

rot = =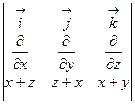(1–1) +(1–1) +(1–1) = ,

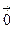что и доказывает потенциальный характер поля .

Найдем потенциал двумя способами.

1 способ.

Для нахождения потенциала воспользуемся формулой (*), беря в качестве М₀ начало координат:

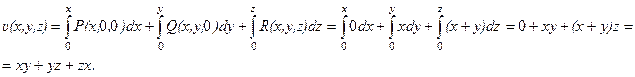
2 способ.

Будем снова считать М₀(0,0,0).

Пусть 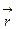=x +y +z – радиус-вектор точки М(x,y,z), а точка N пробегает отрезок M₀М; ее радиус‑вектор 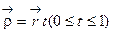. Точка N имеет координаты t_x, t_y, t_z.

Отсюда d 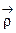= 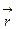dt. Положим .

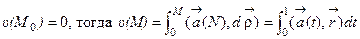Для рассматриваемого поля (t)=t(y+z) + t(z+x) +t(x+y) .

( (t), 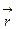)=t(y+z)x+t(z+x)y+t(x+y)z=2t(xy+yz+zx).

Следовательно, 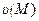=(xy+yz+zx) 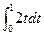= xy+yz+zx.

Ответ: xy+yz+zx.

67. Доказать, что циркуляция потенциального поля по любому замкнутому контуру равна нулю.

Решение: Пусть - потенциальное поле и (L) - замкнутый контур, началом и концом которого является точка М(М=М₀).

Тогда 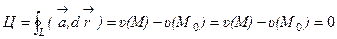, что и требовалось доказать.

Упражнения

68. Пусть 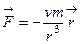– гравитационное поле (поле сил тяготения), которое представляет собой силу притяжения единичной массы, помещенной в точку М, массой m, находящийся в начале координат. Сила определена во всех точках, кроме начала координат и образует векторное поле – поле тяготения точечной массы m. Показать, что поле 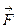потенциально во всем пространстве, кроме начала координат и найти его потенциал.

69. Проверить , что поле =(3yz+x²) + (2y²+3xz) +(z²+3xy) является потенциальным, и найти его потенциал.

70. Доказать, что векторное поле = y² +2xy +z потенциально, и найти его потенциал.

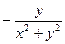
71. Выяснить, является ли векторное поле = + +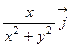2 потенциальным.

72. Даны векторные поля: ₁=(y+z) + (x+z) +(x+y) ; ₂=f(x) + f₂(y) + f₃(z) ; ₃=x + y +y .

Выяснить какие из них являются потенциальными.

73. Проверить, будет ли потенциальным поле . В случае потенциальности поля найти его потенциал u(x,y,z).

а) =(-2x-yz) +(-2y-xz) +(-2z-xy) ;

б) =(2x-yz) +(2y-xz) +(2z-xy) ;

в) =(2x+yz) +(2y+xz) +(2z+xy) ;

г) =(2x-4yz) +(2y-4xz) +(2z-4xy) ;

д) =(2x-3yz) +(2y-3xz) +(2z-3xy) ;

е) =(-3x+yz) +(-3y+xz) +(-3z+xy) ;

ж) =(2x+2yz) +(2y+2xz) +(2z+2xy) ;

з) =(4x+yz) +(2y+xz) +(2z+xy) .