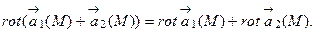Формула Гаусса-Остроградского. Дивергенция

Пусть функции z₁(x,y) и z₂(x,y) определены и непрерывны в ограниченной замкнутой области D и z₁(x,y) £ z₂(x,y). Область G={(x,y,z)|(x,y)ÎD , z₁(x,y) £ z £ z₂(x,y)} называется z–цилиндрической. Аналогично определяются х–цилиндрическая и y–цилиндрическая области. Область G называется простой, если ее можно разбить на конечное число как х–цилиндрических, так и y–цилиндрических и z‑цилиндрических областей.

Теорема. Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z), и их частные производные 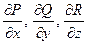непрерывны в простой замкнутой области G, ограниченной кусочно-гладкой поверхностью Ф. Тогда справедлива формула

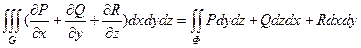, (1)

где поверхностный интеграл берется на внешней стороне поверхности Ф, которая служит границей G.

Формула (1) называется формулой Остроградского-Гаусса.

Следствие. Если функции P, Q, R таковы, что 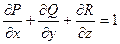, то интеграл в левой части равенства

(1) равен объему области G, т.е. 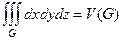, и из формулы (1) получается формула для вычисления объема области G с помощью интеграла по ее поверхности:

(2)

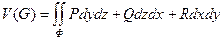
Примеры

34. Пользуясь формулой Остроградского-Гаусса, вычислить интеграл 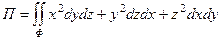, где Ф – внешняя сторона сферы (x–a)²+(y-b)²+(z–c)²=R².

Решение. По формуле Остроградского-Гаусса имеем:

,

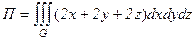где G – шар (x–a)²+(y-b)²+(z–c)²£R². Для вычисления интеграла перейдем к сферическим координатам:

x=a+rcosjsinq, y=b+rsinjsinq, z=c+rcosq, 0 £ j £ 2p, 0 £ q £ p.

Якобиан перехода равен r²sinq. Уравнение границы области G имеет вид r = R. Следовательно, .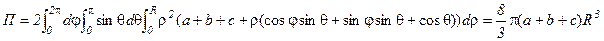

Ответ: .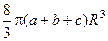

Пусть задана ориентированная поверхность (Ф), т.е. такая поверхность, в каждой точке которой выбран единичный вектор 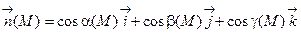, меняющийся на поверхности непрерывно. В случае замкнутой поверхности в качестве будем всегда выбирать вектор внешней нормали.

Потоком П векторного поля 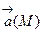через ориентированную поверхность (Ф) называют поверхностный интеграл (первого рода): .

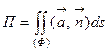Дивергенция (расходимость) векторного поля 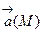может быть определена выражением: 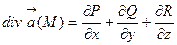, т.е. дивергенция векторного поля 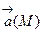представляет собой скалярное поле в области G.

Если 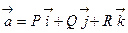– разложение векторного поля 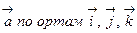, то формулу, определяющую поток, можно записать в виде:

,

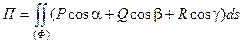либо записать в форме поверхностного интеграла (второго рода):

.

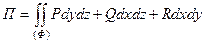Теперь теорему Остроградского-Гаусса можно сформулировать следующим образом: поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции векторного поля по объему, ограниченному этой поверхностью.

35. Найти поток векторного поля 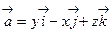через замкнутую поверхность (Ф), состоящую из поверхности конуса x²+y²=z² и плоскости z=1. См. рис 3.

Решение. Имеем .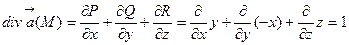

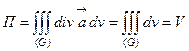Следовательно, , где V–объем конуса.

Так как 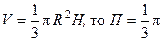. Ответ: p/3.

36. Найти поток векторного поля 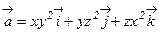через поверхность сферы x²+y²+z²=R².

Решение. В данном случае поверхность (Ф) – замкнутая, поэтому для вычисления потока можно применить формулу Гаусса - Остроградского. Имеем

.

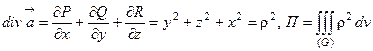Рис. 3.

Вычисляем интеграл в сферических координатах:

.

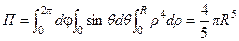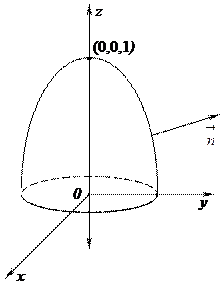
37. Найти поток векторного поля 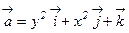через часть поверхности параболоида 1 – z = x²+y² (0 £ z £ 1). См. рис. 4.

Решение. Обозначим данную поверхность через (Ф₁) и рассмотрим замкнутую поверхность 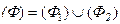, где (Ф₂) – круг радиуса R=1 на плоскости XOY. Из формулы Гаусса - Остроградского вытекает, что поток через поверхность (Ф) равен нулю. Действительно, для данного поля

.

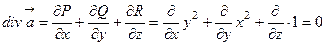Рис. 4

Следовательно, 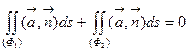. Отсюда искомый поток через поверхность (Ф₁):

.

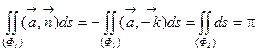Ответ: p.

38. Пользуясь формулой Остроградского-Гаусса, вычислить поток векторного поля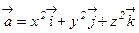

через полную поверхность конуса .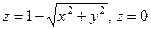

Решение. Найдем дивергенцию векторного поля: 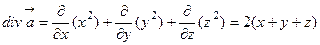. Тогда .

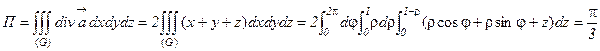Упражнения

Применяя формулу Остроградского-Гаусса, преобразовать поверхностные интегралы в интегралы по объему:

39. .

40. .

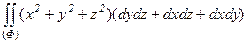41.

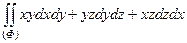
С помощью формулы Остроградского-Гаусса вычислить следующие интегралы:

42.

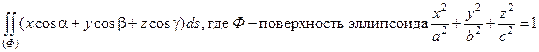
43.

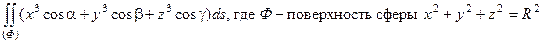
44.

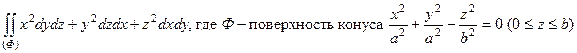
45. Найти дивергенцию вектора .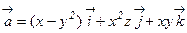

46. Пользуясь формулой Остроградского-Гаусса, преобразовать поверхностный интеграл

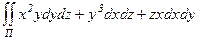в интеграл по объему.

47. Вычислить поверхностный интеграл 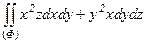, где Ф – полная поверхность параболоида z=x²+y², ограниченного плоскостью z=1.

48. Пользуясь формулой Остроградского–Гаусса, вычислить поверхностные интегралы по внешней стороне поверхности Ф (если поверхность не замкнутая, дополните её до замкнутой).

а) ;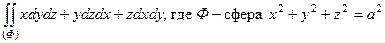

б) ;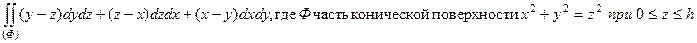

в) ;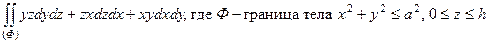

г) ;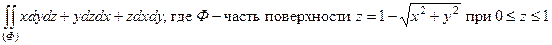

д) 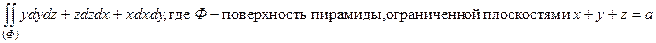(a>0), x=0, y=0, z=0;

е) ;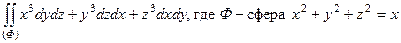

ж) .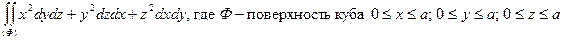

Формула Стокса

Пусть в области G определено векторное поле 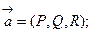L – замкнутый контур, лежащий в области G; Ф- произвольная поверхность, границей которой является контур L; ФÌG (говорят "поверхность Ф натянута на контур L"); 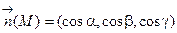–единичный вектор нормали на выбранной стороне поверхности Ф.

Поверхность Ф называется xyz – проектируемой, если она однозначно проектируется на каждую координатную плоскость прямоугольной системы координат Oxyz. Такую поверхность можно задать с помощью любого из уравнений: z=z(x,y), (x,y)Î G₁; x=x(y,z), (y,z)ÎG₂; y=y(z,x), (z,x)Î G₃.

Пусть Ф – гладкая xyz – проектируемая ориентированная поверхность, ограниченная кусочно-гладким контуром L и расположенная внутри области G, в которой функции P(x,y,z), Q(x,y,z), R(x,y,z) имеет непрерывные частные производные первого порядка. Тогда справедлива формула Стокса

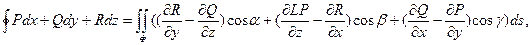
где ориентация контура L согласована с ориентацией поверхности Ф. Левая часть формулы Стокса есть циркуляция векторного поля вдоль контура L, а правая часть представляет собой поток через поверх

ность Ф векторного поля с координатами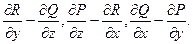

Эта формула названа по имени английского физика и математика Д. Стокса. Её формулу можно переписать также в следующем виде:

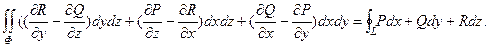
Формула Стокса остается верной для иной ориентированной поверхности Ф с кусочно-гладким краем L , которую можно разбить при помощи кусочно-гладких линий на конечное число гладких кусков, проецирующихся на все три плоскости координат. Ориентированная поверхность, которую можно разбить на конечное число и плоского треугольников, называется полиэдральной поверхностью и представляет собой пример простейшей поверхности, к которой применима формула Стокса.

Примеры

49. Вычислить циркуляцию вектора 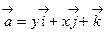вдоль окружности x²+y²=1, z=0 в положительном направлении.

Решение. В этом случае P=y; Q=x; R=1. Следовательно,

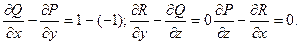
по формуле Стокса

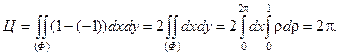
Применяя формулу Стокса, вычислить интегралы:

50 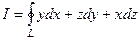, где L - окружность x²+y²+z² a², x+y+z=0, пробегаемая против хода часовой стрелки, если смотреть с положительной оси Ox.

Решение. Применив формулу Стокса и взяв в ней в качестве поверхности Ф круг радиуса а, лежащий в плоскости x+y+z=0, получаем:

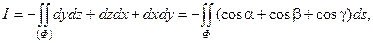
где 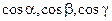- направляющие косинусы нормали к поверхности Ф – плоскости x+y+z=0, так как нормаль этой плоскости образует с положительным направлением оси Oz острый угол, то в каждой из формул для вычисления 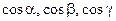перед знаком радикала возьмем знак "+".

Очевидно, 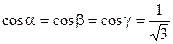, в силу чего имеем:

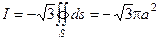
Ответ: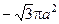

51. 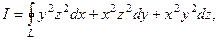L - замкнутая кривая x=acost, y=acos2t, z=acos3t, пробегается в направлении возрастания параметра t.

Решение. При изменении t от 0 до p подвижная точка М(x,y,z) пробегает кривую L от точки M₀(a_,a_,a) до точки M₁(-a_,a_,-a), а при изменении t от p до 2p точка М пробегает ту же самую часть кривой L в противоположном направлении – от точки М, до точки М₀. Таким образом, точки замкнутой кривой L взаимно накладываются и кривая L не ограничивает никакой поверхности, вследствие чего I=0.

Ответ: 0.

Упражнения

52. Интеграл 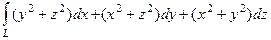, взятый по некоторому замкнутому контуру, преобразовать с помощью формулы Стокса в интеграл по поверхности, "натянутой" на этот контур.

53. Вычислить интеграл 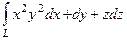, где контур L – окружность x²+y²= R², z=0, используя формулу Стокса, взяв в качестве поверхности полусферу 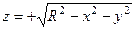. Интегрирование по окружности в плоскости xOy ведется в положительном направлении.

Ротор векторного поля

С понятием циркуляции тесно связано понятие ротора, или вихря. Циркуляция характеризует завихренность векторного поля вдоль всего контура. Локальной характеристикой поля, связанной с завихренностью, является ротор.

Рассмотрим сначала плоское векторное поле и какой-то контур L , окружающий выбранную точку М₀. Величину площади области, заключенной внутри L, обозначим через S. Тогда отношение

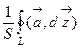(1)

дает среднюю плотность циркуляции вектора на площадке S. Плотность циркуляции в точке М₀ характеризуется пределом выражения (1) при условии стягивания контура L в точку М₀, тогда площадь S, охватываемая контуром L, стремится к нулю, таким образом, если предел 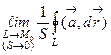существует, то он дает величину завихренности поля в точке М₀.

Если векторное поле - пространственное, то можно говорить о завихренности поля в каком-либо направлении .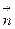

Ротором векторного поля в точке М₀ обозначаемым 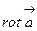называется вектор, проекция которого на каждое направление 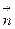равна пределу отношения циркуляции векторного поля по контуру L плоской области G, перпендикулярной этому направлению, к величине площади S этой области, когда размеры площади стремятся к нулю, а сама область стягивается в точку М₀, т.е.

,

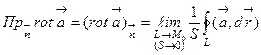где L – контур, лежащий в плоскости, перпендикулярной вектору 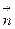, S- площадь области, ограниченной этим контуром.

Если задано векторное поле 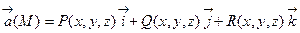, где функции P, Q и R – непре

рывно дифференцируемые в соответствующей области , то

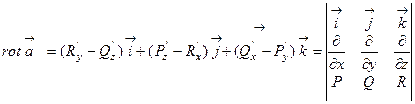
Примеры

54. Найти ротор векторного поля .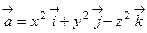

Решение. = = = = 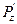= =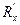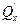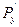0, то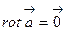

Ответ: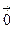

55. Найти rot (grad u), если u=x²+ y²+ z²

Решение. Поскольку grad u = 2x² + 2y² +2z² , то rot (grad u)=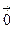

Ответ: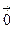

56. Найти ротор поля скоростей твердого тела, вращающегося вокруг неподвижной точки с мгновенной угловой скоростью .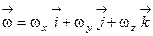

Решение. Как известно, скорость твердого тела определяется по формуле

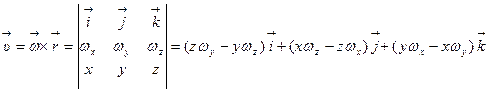
Отсюда находим .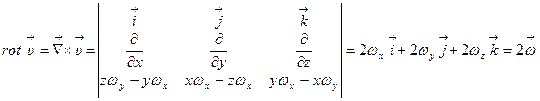

Таким образом, 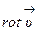, характеризуя "вращательную компоненту" поля скоростей, равен удвоенной скорости вращения.

57. Доказать, что завихренность поля достигает наибольшего значения в направлении ротора.

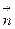Решение. Завихренность поля в направлении равна проекции ротора на это направление, т.е. 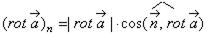.Отсюда видно, что поле наибольшую завихренность имеет в случае, когда 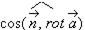=1, а это означает, что направление нормали 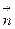совпадает с направлением 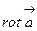, причем наибольшая завихренность равна .

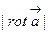58. Вычислить ротор векторного поля: = y² - x² +z² .

Решение .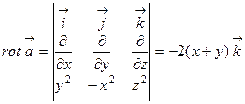

Ответ: .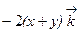

Упражнения

59. Доказать свойства ротора:

а) 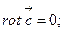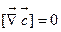, где 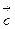=const

б)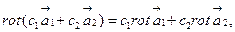

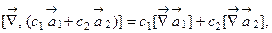где с₁, с₂ – постоянные коэффициенты.

в) 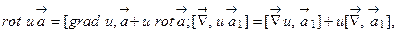где u - скалярное поле.

60. Вычислить ротор векторного поля:

а)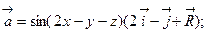

б)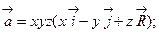

в)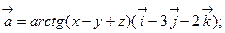

61. Вычислить ротор векторного поля 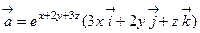в точке М₀(3,-3,1).

62. Найти функцию векторного поля 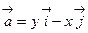вдоль замкнутой линии ABОA, где АВ – дуга астроиды, определяемой уравнением: 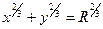или x=Rcos³t, y=Rsin³t.

Указание. Следует применить формулу Стокса:

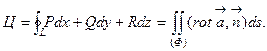
Рис. 4.

3. С помощью формулы Стокса найти циркуляцию векторного поля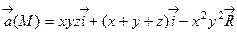

вдоль контура квадрата АВСDА определяемого уравнениями: –x+y=a; x+y=a; x–y=a; x+y=–a; z=0.

64. Вычислить с помощью формулы Стокса циркуляцию векторного поля 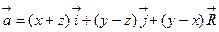вдоль окружностей:

а) (y+1)² +(z–1)²=1, x=5 (вектор положительной нормали );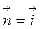

б) (x–3)² +(y–2)²=4, z=0 (вектор положительной нормали )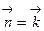

65. Доказать, что