Соленоидальное поле и его свойства

Векторное поле (М) называют соленоидальным в области (G), если во всех точках этой области .

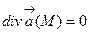С понятием соленоидального поля тесно связано понятие векторного потенциала. Если в области (G), в которой определено поле (М) существует такое векторное поле 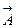(М), что в каждой точке области (G) 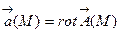, то векторное поле 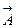(М) называют векторным потенциалом поля (М) в области (G).

Для поля (М), обладающего векторным потенциалом в области (G), поток через любую замкнутую поверхность, содержащуюся в области (G), равен нулю.

Поле (М), обладающее векторным потенциалом в области (G), является в ней соленоидальным . Обратное, вообще говоря, неверно: для произвольно взятой области (G) соленоидальность поля (М) еще не гарантирует существования во всей области (G) векторного потенциала поля (М). Однако, если ограничиться пространственно-односвязными областями, то соленоидальность поля и наличие у него векторного потенциала являются эквивалентными свойствами. Таким образом, в пространственно-односвязной области условие div =0 является необходимым и достаточным для существования векторного потенциала.

Из формулы Остроградского-Гаусса следует, что если соленоидальное поле задано в односвязной области, то поток вектора через любую замкнутую поверхность, принадлежащую этой области, равен нулю:

.

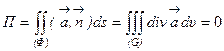Пусть соленоидальное поле задано в односвязной области. Тогда поток вектора через любую поверхность S, натянутую на заданный контур L, не зависит от вида этой поверхности, а зависит только от контура L.

Возьмем в поле замкнутый контур L и проведем через его точки векторные линии. Образовавшаяся поверхность называется векторной трубкой. Любая другая векторная линия, не проходящая через точки контура L , либо целиком лежит в векторной трубке, либо находится вне ее. В случае поля скоростей стационарного потока жидкостей векторная трубка – это та часть пространства, которую запасной при своем перемещении фиксированный объем жидкости.

Интенсивностью векторной трубки называется поток поля через поперечное сечение этой трубки. Для соленоидальных полей имеет место так называемый закон сохранения интенсивности векторной трубки.

Если соленоидальное поле определено в односвязной области G, то интенсивность векторной трубки постоянна вдоль всей трубки.

В соленоидальном поле векторные линии не могут ни начинаться, ни кончаться внутри поля; они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви (в случае неограниченного поля).

Упражнения

75. Проверить, будут ли соленоидальными поля, указанные в задаче 74.

Векторный потенциал

Векторный потенциал 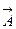(М) определяется с точностью до градиента произвольного соленоидального поля f(М).

В самом деле, если rot 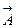(М)= (М) и f(M) – произвольное скалярное поле, то поскольку rot grad f(M)=0, получаем rot( 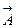(М)+grad f(M)) = rot 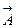(М)+ rot grad f(M)= (М).

Для того чтобы непрерывно дифференцируемое поле (М) было соленоидальным, необходимо и достаточно, чтобы оно имело векторный потенциал 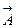(М). Необходимость этого условия является следствием разрешимости системы дифференциальных уравнений:

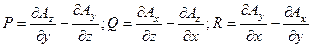(1)

при условии div =0 ( ).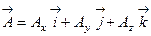

Покажем как можно найти векторный потенциал 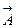(М). поскольку в выборе этого вектора имеется значительная доля произвола примем A_x=0. Тогда система (1) примет вид

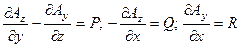(2)

Таким образом, задача сводиться к определению функции A_y и A_z, удовлетворяющих условиям (2) при условии, что известные функции P, Q, R таковы, что div =0. Пусть М₀(x₀,y₀,z₀) – фиксированная, М(x,y,z) – произвольные точки параллелепипеда W.

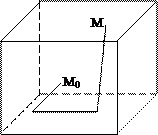Рис. 6.

Рассмотрим функции

A_y(x,y,z)= 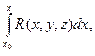A_z(x,y,z)= 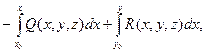(3)

Условие задания поля (М) в параллелепипеде с гранями, параллельными плоскостям координат, гарантирует, что пути интегрирования в этих формулах не выйдут за пределы поля. Применяя правила дифференцирования определенного интеграла по параметру и по верхнему пределу и принимая во внимание условие div =0 , получим , что обе функции A_y и A_z, определенные равенствами (3) удовлетворяют и первому из условий (2). Таким образом, 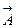= А_х + A_y +A_z , координаты A_y и A_z определяются формулами (3). Для этого вектора 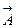выполняется условие rot = .

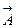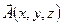74. Найти векторный потенцал

для соленоидального поля, задаваемого вектором а = 2уi - zj + 2хk.

Ответы:

10. Область определения – круг x²+y²£9; линии уровня – семейство концентрических окружностей

x²+y²=9–с² (|с| £ 3).

11. Поле определено во всем пространстве, за исключением точки r=0; поверхности уровня –сферы r=c c центром в точке, где находится заряд.

12.Поле определено в области z²+y²–x²³0;поверхности уровня – круговые конусы а²(z²+y²)–x²=0 (|а| £ 1).

13. Линии уровня u=c представляют собой семейство гипербол x²–y²=(–1)ⁿ arcsin c +pn, где n–целое число.

14. Поле определено во всем пространстве, за исключением плоскости z=0; поверхности уровня – параболоиды вращения x² +y²=сz (–¥<c<¥).

15. а) –4 +2 –4 . б) 12 – ; в) + .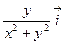

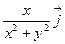16. Прямые, проходящие через начало координат.

17. x² -y²=с; z=h.

18. x³ +y³=c₁; z³ +y³=c₂.

19. y=c₁z; x² +y²+ z²= c₂y.

20. Окружности, лежащие в плоскостях, перпендикулярных к прямой, проходящей через начало координат и имеющей направление вектора 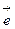; центры этих окружностей лежат на этой прямой.

22. Окружности с центром на оси Оy , проходящей через начало координат.

23. Направление наибыстрейшего возрастания функции в точке (0,0) совпадает с положительным направлением оси Оy.

24. 1) tgj »0,342, j »18⁰52’; 2) tgj »4,87, j »78⁰24’.

25. Отрицательная полуось оси Оy.

26. 1) cosa »0,99; a=8⁰; 2) cosa » –0,199; a=101⁰30’;

30. Ц= –pb².

31. Ц= –p.

32. Ц= 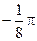R⁶

33. а) Ц=2p; б) Y=2p.

39. .

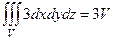40.

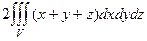
41.0.

42. 4pabc.

43. .

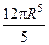44. .

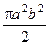45. 1.

46. .

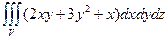47. .

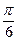48. a) 4pa³; б) 0. Дополните поверхность S до замкнутой; в)0; г) p. Дополните поверхность S до замкнутой; д)0; е) 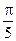; ж) 3а⁴.

52.

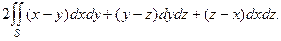
53. .

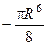60. а) rot = –2cos(2x–y–z)( +2 ); б) rot =x(z²-y²) + y(x²-z²) + z(y²-x²) ; в) rot = .

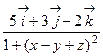61. 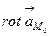=20 +26 –24 .

62. .

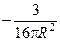63.–2a² .

64. а) Ц=2p; б) Ц=0.

68. .

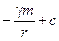69. 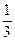(x³+2y³+z³)+3xyz + c.

70.

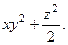
71. Нет.

72. Потенциальными являются поля 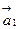и .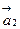

73. 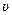(x,y,z)=xyz(x+y+z)+c, где с произвольная постоянная.

74. х²j + (хz + y²)k.

Литература

1. Государственный образовательный стандарт высшего профессионального образования. М.: Госкомвуз России, 2000.

2. Никольский С.М. Курс математического анализа, том. II- М.: Наука, 1973.

3. Зорич В.А. Математический анализ. Ч. II.- М.: Наука, 1984

4. Уваров В.Б. Математический анализ. М.: Высш.шк.,1984.

5. Ефимов А.В. и др. Математический анализ (специальные разделы) ч.II. Применение некоторых методов математического и функционального анализа. - М.: Высш. шк., 1980.

6. Кальницкий Л.А и др. Специальный курс высшей математики для вутзов. М.: Высш. шк., 1976.

7. Несис Е.И. Методы математической физики. - М.: Просвещение, 1977.

8. Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Наука, 1972.

9. Берман Г.Н. Сборник задач по курсу математического анализа. - М.: Наука, 1985.

10. Бутузов В.Ф. и др. Математический анализ в вопросах и задачах. Функции нескольких переменных. - М.: Высш. шк. ,1988.

11. Филиппенко В.И. Приложения кратных интегралов. – Кривой Рог, 1998.

12. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. – М.: Изд – во МГТУ им. Н.Э.Баумана, 2001.