Вопрос 7. Функция. Предел функции.

Любой предел состоит из трех частей:

1) Всем известного значка предела .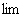
2) Записи под значком предела, в данном случае 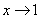. Запись читается «икс стремится к единице». Чаще всего – именно 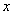, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ( ).
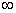3) Функции под знаком предела, в данном случае .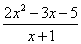

Сама запись 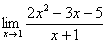читается так: «предел функции 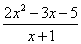при икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 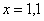, затем , , …, , ….
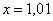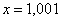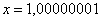То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

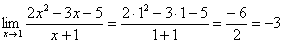
Готово.

Итак, первое правило:Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

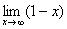
Разбираемся, что такое 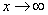? Это тот случай, когда 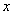неограниченно возрастает, то есть: сначала 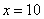, потом 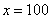, потом 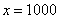, затем 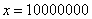и так далее до бесконечности.

А что в это время происходит с функцией ?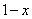
, , , …

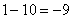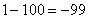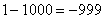Итак: если 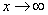, то функция 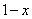стремится к минус бесконечности:

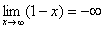
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 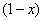бесконечность и получаем ответ.

Еще один пример с бесконечностью:

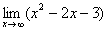
Опять начинаем увеличивать 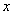до бесконечности и смотрим на поведение функции:

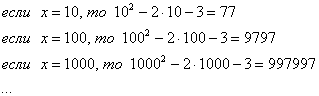
Вывод: при 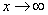функция 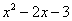неограниченно возрастает:

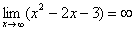
Пределы с неопределенностью вида 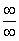и метод их решения

Сейчас мы рассмотрим группу пределов, когда 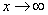, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример:

Вычислить предел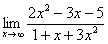

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 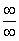. Можно было бы подумать, что 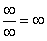, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим 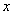в старшей степени:

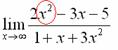
Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим 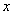в старшей степени:

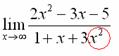
Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 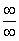необходимо разделить числитель и знаменатель на 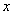в старшей степени.

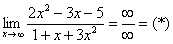
Разделим числитель и знаменатель на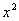

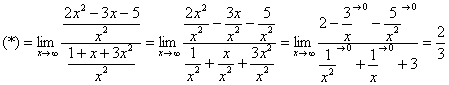
Вот оно как, ответ 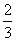, а вовсе не бесконечность.

Пределы с неопределенностью вида 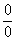и метод их решения

Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Пример 4

Решить предел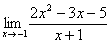
Сначала попробуем подставить -1 в дробь:

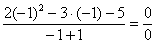
В данном случае получена так называемая неопределенность .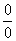

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 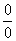, то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

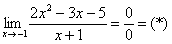
Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

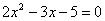
Сначала находим дискриминант:

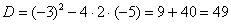
И квадратный корень из него: .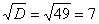

В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни:

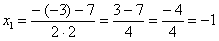
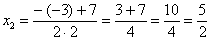
Таким образом:

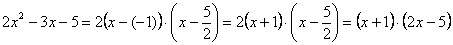
Всё. Числитель на множители разложен.

Знаменатель. Знаменатель 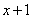уже является простейшим множителем, и упростить его никак нельзя.

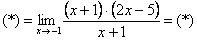
Очевидно, что можно сократить на :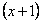

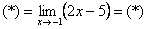
Теперь и подставляем -1 в выражение, которое осталось под знаком предела: