Отображения множеств (функции). Предел и непрерывность функции в точке. Методика введения понятия «функция» в школьном курсе математики.

Опр-ие. Пусть А и В – произвольные множества. Отображением множества А в множество В называют правило (соответствие), которое каждому элементу множества А ставит в соответствие единственный для этого элемента элемент множества В.

Обозначение. f: A→B. Здесь, f– имя (наименование) отображения. Если a A– элемент множества А, то элемент множества В, который ставится ему в соответствие при этом отображении обозначают f(A) и пишут a A→f(a) B. Элемент f(a) называют значением отображения 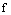"в точке а" или образом элемента а. При этом сам элемент а называют прообразом элемента f(a).

Замечание. Слова отображение и функция являются синонимами, при этом множество А называют областью определения функции (отображения) f и обозначают Domf=D(f), а множество значений f обозначают Imf и называют образом отображения f. Imf является подмножеством множества В: .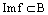

Отображение f называется инъективным отображением, если ∀y∈Y y=f(x)является образом единственного x.Отображение f называется сюръективным отображением, если все элементы в множестве Y являются образами какого-либо x. (Это отображение множества X на множество Y).Отображение ff называется биективным, если оно инъективно и сюръективно, в противном случае такое отображение назвается взаимно однозначным соответствием.

Определение. Множества X и Y называются эквивалентными (равномощными), если они находятся во взаимно однозначном соответствии.

Предел и непрерывность функции в точке.

Опр 1. Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е. 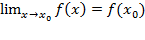(1)

Таким образом, условие непрерывности функции y=f(x) в точке х₀ состоит в том, что:

1) значение функции в точке х=х₀ есть определённое число f(x₀);

2) предел функции y=f(x) при стремлении х к х₀ как слева, так и справа, есть одно и то же определённое число ;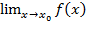

3) числа 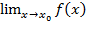и f(x₀) равны.

Так как 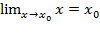, то равенство (1) можно записать в виде 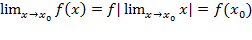(2)

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, т.е. в функцию f(x) вместо аргумента х подставить его предельное значение х₀.

Опр2. Функция y=f(x) называется непрерывной в точке х₀, если она определена в точке х₀ и её окрестности, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Свойства функций, непрервных в точке

1. Если функции f(x) и φ(x) непрерывны в точке х₀, то их сумма f(x) + φ(x), произведение f(x)*φ(x) и частное f(x)/φ(x) (при условии φ(x₀) ≠0) являются функциями, непрерывными в точке х₀.

2. Если функция у=f(x) непрерывна в точке х₀ и f(x₀)>0, то существует такая окрестность точки х₀, в которой f(x)>0.

3. Если функция у=f(u) непрерывна в точке u₀, а функция u=φ(x) непрерывна в точкеu₀=φ(x₀), то сложная функция y=f[φ(x)] непрерывна в точке х₀.