Сложение и вычитание матриц.

Сложение и вычитание матриц.

Суммой A+B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij+bij для всех i=1,mи j=1,n.

Аналогичное определение вводят и для разности матриц:

Разностью A−B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij−bij для всех i=1,m и j=1,n.

Умножение матрицы на число.

Произведением матрицы Am×n=(aij) на число α называется матрица Bm×n=(bij), где bij=α⋅aijдля всех i=1,m¯¯¯¯¯¯¯¯ и j=1,n¯¯¯¯¯¯¯.

Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.

Произведение двух матриц.

Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.

Произведением матрицы Am×n=(aij) на матрицу Bn×k=(bij) называется матрица Cm×k=(cij), для которой каждый элемент cij равен сумме произведений соответствующих элементов i-й строки матрицы Aна элементы j-го столбца матрицы B:

Вопрос 2. Определители квадратных матриц. Свойства определителей.

Определитель матрицы - это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать.

I. Определитель матрицы первого порядка

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент а₁₁:

.

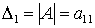II. Определитель матрицы второго порядка

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

.

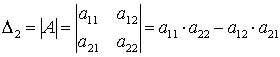Например, пусть

.

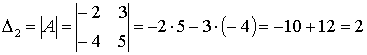III. Определитель матрицы третьего порядка

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

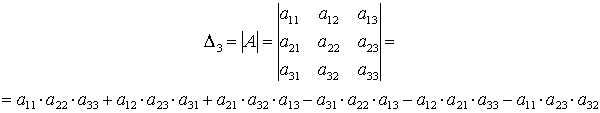
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

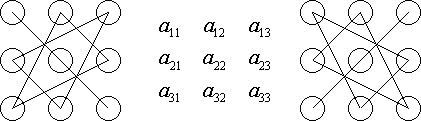
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Пример. Вычислить определитель третьего порядка:

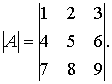
Решение.

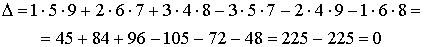
Определитель матрица, которого более высокого порядка лучше всего находить через приведение к треугольному виду матрицы.

Вопрос 3. Обратная матрица. Элементарные преобразования.

Для применения этого метода в одну матрицу записывают заданную матрицу A и единичную матрицу E, т.е. составляют матрицу вида (A|E) (эту матрицу называют также расширенной).

К элементарным преобразованиям в данной ситуации относят такие действия:

1. Смена мест двух строк.

2. Умножение всех элементов строки на некоторое число, не равное нулю.

3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.

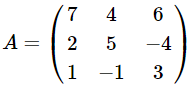Пример

Найти матрицу A⁻¹, если

Решение

В этом примере будет найдена обратная матрица методом Гаусса. Расширенная матрица, имеющая в общем случае вид (A|E), в данном примере примет такую форму:

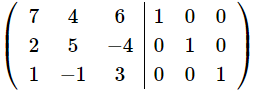
Вопрос 6. Метод Гаусса.

На первом этапе нужно записать расширенную матрицу системы:
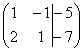. По какому принципу записаны коэффициенты, думаю, всем видно.

Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: 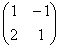. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: .

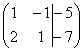Вернемся к нашей системе 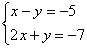. Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

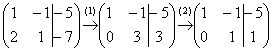
В результате элементарных преобразований получена эквивалентная исходной система уравнений:

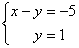
В нижнем уравнении у нас уже готовый результат: .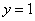

Рассмотрим первое уравнение системы 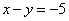и подставим в него уже известное значение «игрек»:

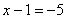
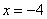
Ответ: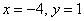

Пример

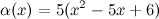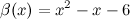Задание. Проверить, являются ли функции и эквивалентными бесконечно малыми при .

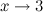Решение. Проверим вначале, что данные функции являютсябесконечно малыми функциями в точке :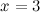

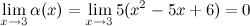
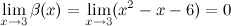
Найдем предел отношения этих функций:

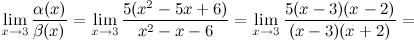
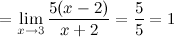
Ответ. Заданные функци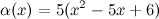и и 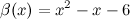являются эквивалентными бесконечно малыми.

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.

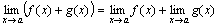Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть 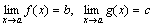.Тогда f(x)=b+α(x)и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

.

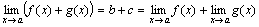Пример. .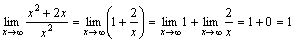

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

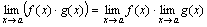Доказательство. Пусть 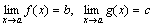. Следовательно, f(x)=b+α(x) иg(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .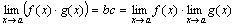

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

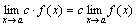Следствие 2. Предел степени равен степени предела:

.

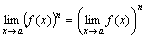Пример. .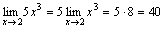

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

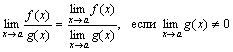Доказательство. Пусть 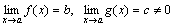. Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

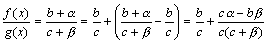Дробь 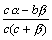является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c²≠0.

Примеры.

1. .
2. .
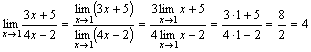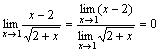3. Рассмотрим 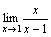. При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как 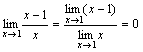, т.е. 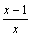есть бесконечно малая функция при x→1, то .

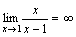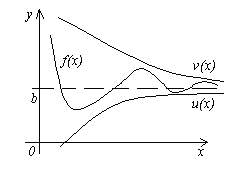Теорема 4. Пусть даны три функции f(x), u(x) иv(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x)стремится к тому же пределу, т.е. если

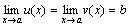, то .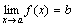

Смысл этой теоремы понятен из рисунка.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента xудовлетворяют неравенству f(x)≥ g(x) и имеют пределы 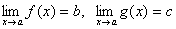, то имеет место неравенство b≥c.

Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 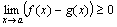, или .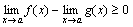

Пример

Задание. Исследовать на непрерывность функцию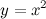

Решение. Функция 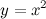определена в любой точке из 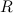. Найдем приращение заданной функции 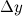произвольной точке :

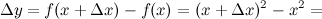
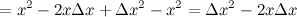
Тогда

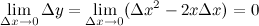
А тогда делаем вывод, что функция 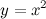является непрерывной.

Ответ. Функция 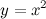является непрерывной.

Правила дифференцирования.

Если у функций f(x) и g(x) существуют производные, то

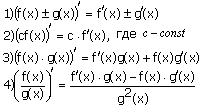
Производная сложной функции:

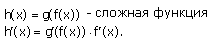
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке

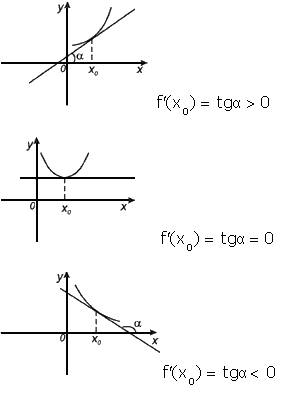
Уравнение касательной к графику функции y=f(x) в точке x₀ :

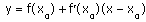
Пример

Задание. Найти наибольшее и наименьшее значение функции 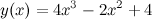на отрезке .

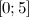Решение. Находим производную функции:

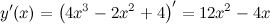
Находим точки, в которых производная равна нулю:

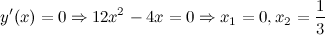
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку 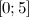. Оба значения лежат в этом промежутке.

Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:

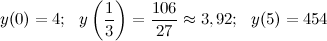
Таким образом,

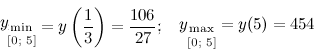
Ответ.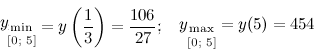

Пример

Задание. Найти интервалы выпуклости/вогнутости функции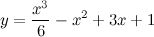

Решение. Найдем вторую производную заданной функции:

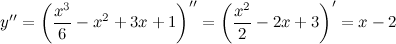
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение :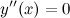

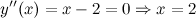
Исследуем знак второй производной слева и справа от полученной точки:

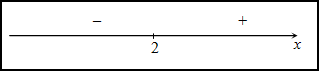
Так как на промежутке 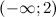вторая производная 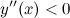, то на этом промежутке функция 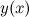выпукла; в силу того, что на промежутке 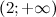вторая производная 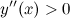- функция вогнута. Так как при переходе через точку 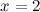вторая производная сменила знак, то эта точка является точкой перегиба графика функции.

Ответ. Точка 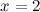- точка перегиба графика функции.

На промежутке 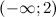функция выпукла, на промежутке 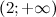функция вогнута.

Определение

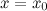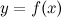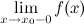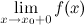Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно 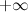или .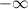

Замечание. Прямая 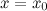не может быть вертикальной асимптотой, если функция непрерывна в точке 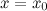. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

Определение

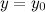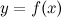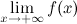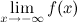Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений или равно .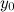

Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.

Определение

Прямая 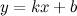называется наклонной асимптотой графика функции 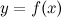, если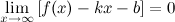

Замечание

(условиях существования наклонной асимптоты)

Если для функции 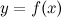существуют пределы 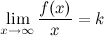и 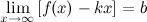, то функция имеет наклонную асимптоту 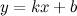при .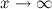

Замечание

Горизонтальная асимптота является частным случаем наклонной при .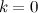

Замечание

Если при нахождении горизонтальной асимптоты получается, что 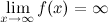, то функция может иметь наклонную асимптоту.

Замечание

Кривая 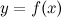может пересекать свою асимптоту, причем неоднократно.

Задание. Найти асимптоты графика функции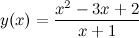

Решение. Область определения функции:

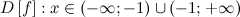
а) вертикальные асимптоты: прямая 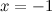- вертикальная асимптота, так как

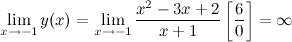
б) горизонтальные асимптоты: находим предел функции на бесконечности:

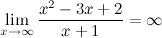
то есть, горизонтальных асимптот нет.

в) наклонные асимптоты :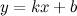

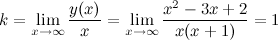
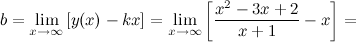
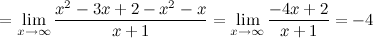
Таким образом, наклонная асимптота: .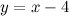

Ответ. Вертикальная асимптота - прямая .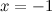

Наклонная асимптота - прямая .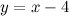

Замечание

Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика.

Замечание

Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них.

Замечание

Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.

Задание. Исследовать функцию 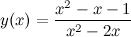и построить ее график.

Решение. 1) Область определения функции.

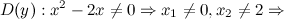
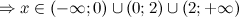
2) Четность, нечетность.

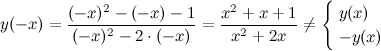
Функция общего вида.

3) Точки пересечения с осями.

а) с осью :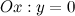

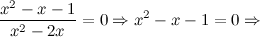
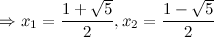
то есть точки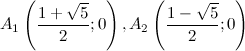

б) с осью 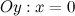: в данной точке функция неопределенна.

4) Асимптоты.

а) вертикальные: прямые 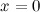и 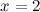- вертикальные асимптоты.

б) горизонтальные асимптоты:

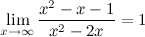
то есть прямая 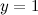- горизонтальная асимптота.

в) наклонные асимптоты :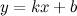

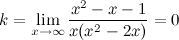
Таким образом, наклонных асимптот нет.

5) Критические точки функции, интервалы возрастания, убывания.

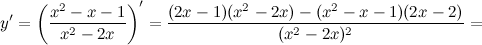
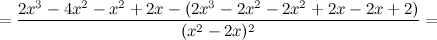
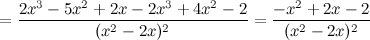
Найдем точки, в которых первая производная равна нулю или не существует: 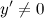для любого из области определения функции; 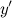не существует пр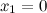и и .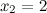

Таким образом, функция убывает на всей области существования.Точек экстремума нет.

6) Точки перегиба, интервалы выпуклости, вогнутости.

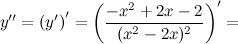
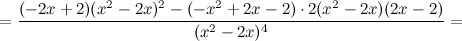
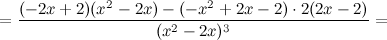
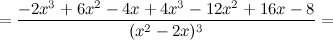
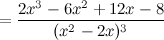
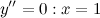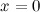Найдем точки, в которых вторая производная равна нулю или не существует: ; при и 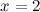вторая производная не существует.

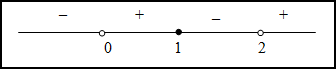
Таким образом, на промежутках 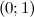и 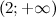функция вогнута, а на промежутках 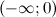и 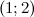- выпукла. Так как при переходе через точку 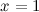вторая производная поменяла знак, то эта точка является точкой перегиба.

7) Эскиз графика.

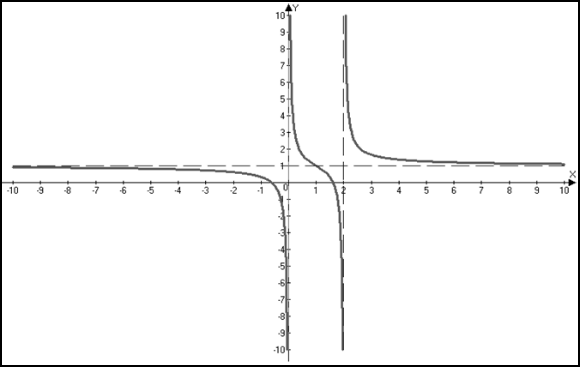
Пример

Функция 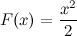является первообразной для функции 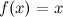, так как

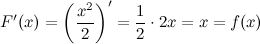
Совокупность всех первообразных функции 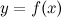, определенных на заданном промежутке, называется неопределенным интегралом от функции 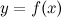и обозначается символом 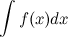. То есть

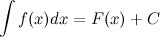
Знак 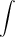называется интегралом, 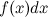- подынтегральным выражением, 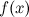- подынтегральной функцией, а - переменной интегрирования.

Пример

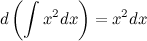
2. Производная от неопределенного интеграла равна подынтегральной функции

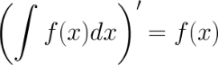
Пример

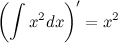
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

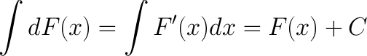
Пример

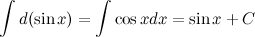
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла

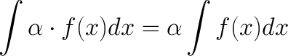
Пример

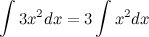
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций

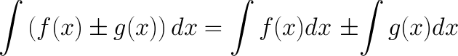
Пример

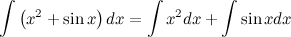
6. Если 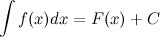, то и 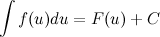, где функция 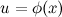- произвольная функция с непрерывной производной.

Пример

Известно, что 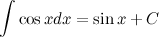, а тогда

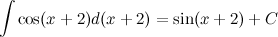
Основные формулы

Замечание

После нахождения интеграла по новой переменной 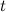необходимо вернуться к первоначальной переменной .

Замечание

В некоторых случаях целесообразно делать подстановку 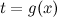, тогда

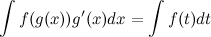
Пример

Задание. Найти интеграл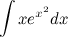

Решение. Сделаем замену переменной: 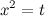, далее приведем интеграл к табличному виду и решим его. В конце решения делаем обратную замену.

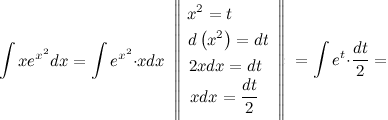
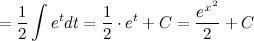
Ответ.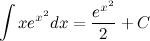

Замечание

В некоторых случаях формулу интегрирования частями нужно применять неоднократно.

Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:

1) ; ;

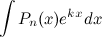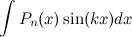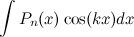
Здесь 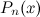- многочлен степени 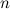, 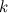- некоторая константа. В данном случае в качестве функции берется многочлен, а в качестве 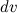- оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется 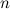раз.

Примеры решения интегралов данным методом

Пример

Задание. Найти интеграл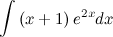

Решение. В исходном интеграле выделим функции и , затем выполним интегрирование по частям.

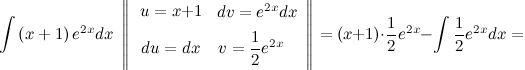
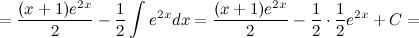
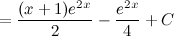
Ответ.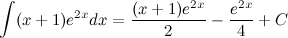

Вопрос 28. Основные понятия теории вероятностей.

Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание.

Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: {выпало 66} и {выпало не 66}, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).

Испытанием называется эксперимент с очерченным набором возможных взаимоисключающих результатов. Эти результаты называются исходами.

Случайное событие — это подмножество множества исходов испытания.

Любое случайное событие может состоять из одного или нескольких исходов испытания (тогда это событие возможно) или не содержать ни одного исхода (невозможное событие). Например, "выпало больше 77" — невозможное событие для испытания "бросание кубика". Отдельно определяют достоверное событие, то есть такое, которое включает в себя все исходы данного испытания.

Исходы, входящие в событие, называются благоприятными для этого события.

Итак, пусть у нас есть испытание с определённым набором равновозможных исходов. Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.

Свойства м(х)

1. Математическое ожидание постоянной величины равно самой постоянной, т.е. М(С) = С, С = const.

С имеет одно значение, равноеС,с вероятностьюp = 1,М(С)=С ^.1 = С.

Определим произведение постоянной СнаХкак дискретную случайную величину 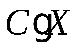, возможные значения которой равны произведениямСна возможные значенияХ. Вероятность 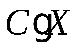равна вероятностямХ. Например, если 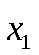имеет вероятность 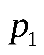, то 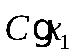имеет также вероятность .

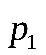2. М(СХ) = С ^. М(Х) – константу можно выносить за знак математического ожидания. Пусть случайная дискретная величинаX задана законом распределения:

		…
		…

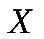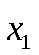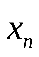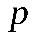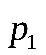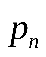Тогда 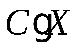имеет закон распределения:

		…
		…

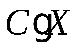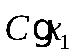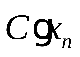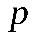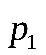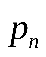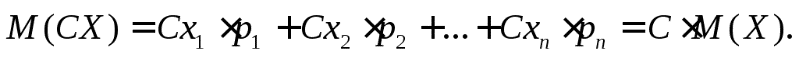
Случайные величины XиYназываютнезависимыми, если закон распределения одной из них не зависит от того, какие значения принимает другая.

Произведение 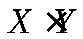– случайная величинаXY, возможные значения которой равны произведениям каждого возможного значенияХна каждое возможное значениеY. ВероятностиXY равны произведению соответствующих вероятностейXиY.

3. 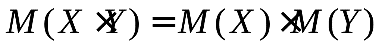, гдеX,Y– независимые дискретные случайные величины.

Пусть законы распределения вероятностей этих величин:

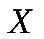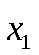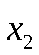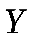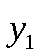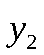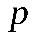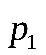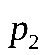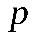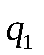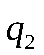Составим значения, которые могут принимать 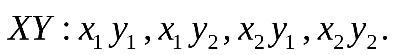Закон распределения:

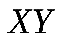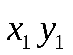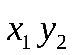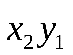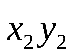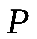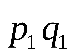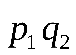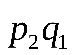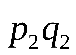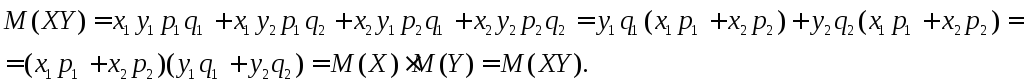
4. M(X+Y) = M(X) + M(Y).

Возможные значения случайной величины X+Yравна сумме возможных значенийXиY, а вероятностьX+Yравна произведению вероятностей слагаемых.

Теорема.М(Х) числа появлений событийАвnнезависимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытанииp.

Иначе, М(Х) биноминального распределения равно .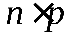

Сложение и вычитание матриц.

Суммой A+B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij+bij для всех i=1,mи j=1,n.

Аналогичное определение вводят и для разности матриц:

Разностью A−B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij−bij для всех i=1,m и j=1,n.

Умножение матрицы на число.

Произведением матрицы Am×n=(aij) на число α называется матрица Bm×n=(bij), где bij=α⋅aijдля всех i=1,m¯¯¯¯¯¯¯¯ и j=1,n¯¯¯¯¯¯¯.

Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.

Произведение двух матриц.

Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.

Произведением матрицы Am×n=(aij) на матрицу Bn×k=(bij) называется матрица Cm×k=(cij), для которой каждый элемент cij равен сумме произведений соответствующих элементов i-й строки матрицы Aна элементы j-го столбца матрицы B: