Разложение квадратного трехчлена на множители
Квадратным трехчленом называется многочлен вида 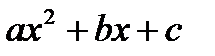 , где
, где
x – переменная, a, b, c – числа, причем а ≠ 0.
Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю.
Квадратный трехчлен имеет те же корни, что и квадратное уравнение 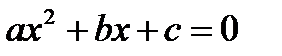 . Так же применима теорема Виета.
. Так же применима теорема Виета.
Теорема: Если x1 и x2 – корни квадратного трехчлена 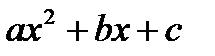 , его можно разложить на множители:
, его можно разложить на множители: 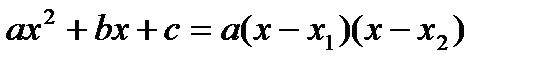 .
.
Доказательство:
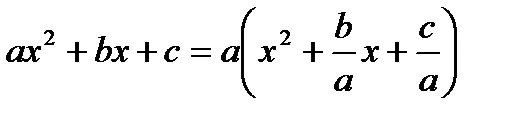 . По теореме Виета
. По теореме Виета 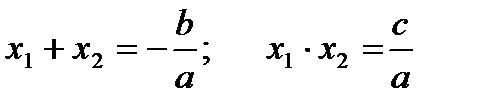
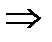
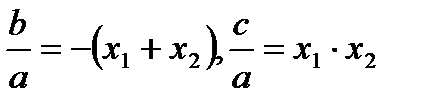
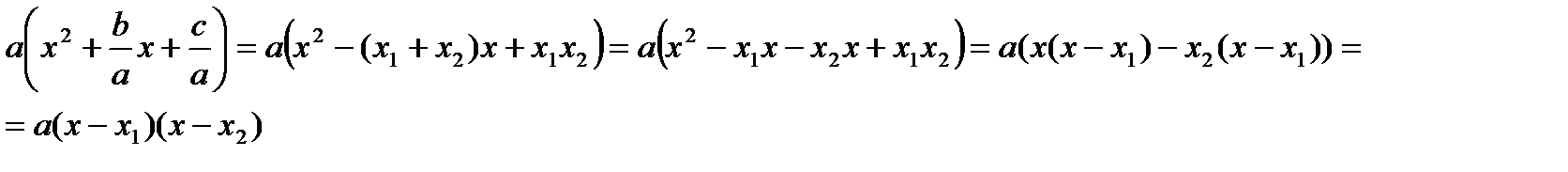 Теорема доказана.
Теорема доказана.
Если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
Уравнения с несколькими неизвестными. Системы уравнений
Уравнение вида f(x; y)=0 называется уравнением с двумя переменными.
Решением уравнения с двумя переменными называется пара значений переменных, обращающих уравнение в верное равенство. Обычно решение записывают в виде пары чисел (x0; y0).
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное числовое равенство.
Уравнение вида 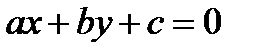 , где x, y – переменные, a, b, c – действительные числа, называется линейным.
, где x, y – переменные, a, b, c – действительные числа, называется линейным.
Если ставится задача найти все общие решения двух уравнений с двумя переменными, то говорят, что надо решить систему уравнений.
Решением системы уравнений с двумя переменными называется пара значений переменных, удовлетворяющих каждому из уравнений.
Решить систему уравнений – значит найти все ее решения или установить, что их нет.
Две системы уравнений называют равносильными, если они имеют одни и те же решения.
Система линейных уравнений с двумя переменными имеет вид 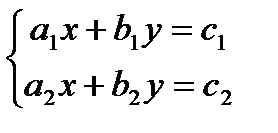 .
.
Не решая систему линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
1. Если 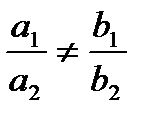 , т.е. коэффициенты при x и y не пропорциональны, то система имеет одно решение. Графически – прямые пересекаются.
, т.е. коэффициенты при x и y не пропорциональны, то система имеет одно решение. Графически – прямые пересекаются.
2. Если 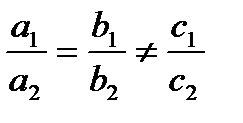 , т.е. коэффициенты при x и y пропорциональны, а свободные члены нет, то система не имеет решений. Графически – прямые параллельны.
, т.е. коэффициенты при x и y пропорциональны, а свободные члены нет, то система не имеет решений. Графически – прямые параллельны.
3. Если 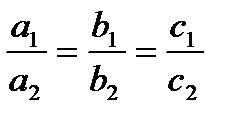 , т.е. все коэффициенты пропорциональны, то система имеет множество решений. Графически – прямые совпадают.
, т.е. все коэффициенты пропорциональны, то система имеет множество решений. Графически – прямые совпадают.
Методы решения систем уравнений:
1. Метод подстановки.
2. Метод алгебраического сложения.
3. Графический метод.
4. Метод введения новых переменных.
Неравенства и их свойства
Запись, в которой два числа или два выражения, содержащие переменные, соединены знаком >, <, ≥, ≤ называется неравенством.
Неравенства, составленные с помощью знаков >, < называются строгими; неравенства, составленные с помощью знаков≥, ≤, называются нестрогими.
Два неравенства вида a > b и c > d называются неравенствами одинакового смысла; а вида a > b, c < d неравенствами противоположного смысла.
Вместо двух неравенств x < a, a < y используется запись x < a < y – двойное неравенство.
Неравенства, содержащие только числа, называются числовыми неравенствами.
Решить неравенство, содержащее переменную, это значит найти множество значений переменной, при котором это неравенство является верным. Элементы этого множества называются решением неравенства.
Два неравенства называются равносильными, если множества их решений совпадают.
Свойства:
1. Если a > b, то b < a.
2. Если a > b и b > c, то a > c.
3. Если к обеим частям верного неравенства прибавить одно и то же число, то получим верное неравенство: a > b => a + c > b + c.
4. Если из одной части верного неравенства перенести в другую какое-либо слагаемое, переменив его знак на противоположный, то получим верное неравенство: a + b > c => a – c > -b.
5. Если обе части верного неравенства умножить на одно и то же положительное число, то получим верное неравенство: a > b, n > 0 => na > nb ( 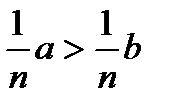 ).
).
6. Если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получим верное неравенство: a > b, n < 0 =>
na < nb ( 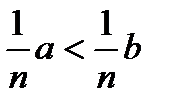 ).
).
7. Неравенства одного смысла можно почленно складывать: a > b, c > d =>a + c > b + d
8. Неравенства противоположного смысла можно почленно вычитать:
a > b, c < d => a - c > b - d
9. Если a > b > 0, c > d > 0 => ac > bd.
10. Обе части неравенства можно возводить в одну и ту же натуральную степень: a > b > 0, m 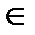 N => am > bm.
N => am > bm.
11. Из каждой части неравенства можно извлекать корень одной и той же натуральной степени: a > b > 0, m 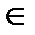 N =>
N => 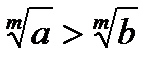 .
.
Решение линейных неравенств
Линейным неравенством называется неравенство вида 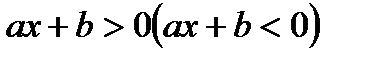 .
.
Если a>0, то неравенство 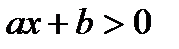 равносильно неравенству
равносильно неравенству 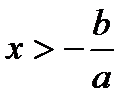 .
.
Если a<0, то неравенство 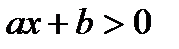 равносильно неравенству
равносильно неравенству 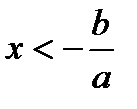 .
.
Например:
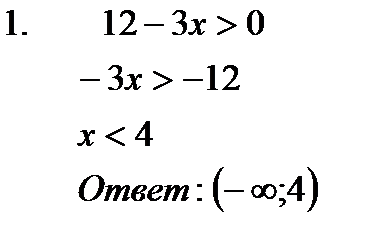 | 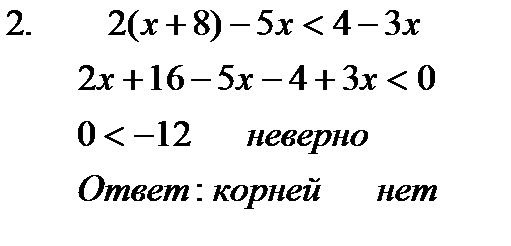 | 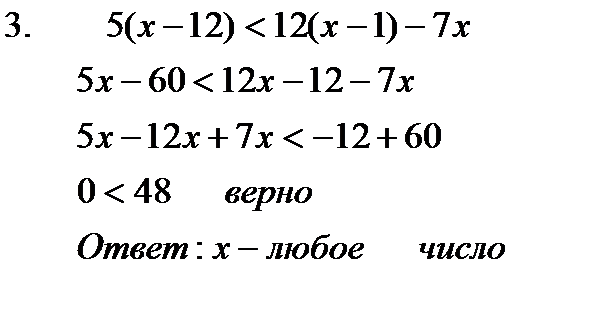 |
