Разложение многочленов на неприводимые множители.

Пусть f(x) ÎP[x], степень f(x) ≥ 1, очевидно, что a │ f(x), aÎP, a ≠ 0.

Определение. Многочлен f(x) называется приводимым над полем Р, если в P[x] существуют делители f(x), степени которых больше нуля, и ≠ cm.f, т.е.: f(x)=f1(x)f2(x), причём deg f2 <deg f, deg f1<deg f .

Многочлен f(x) называется неприводимым над полем Р в противном случае, т.е. один из многочленов f1(x) или f2(x) нулевой степени, если f(x)=f1(x)f2(x).

Замечание. Неприводимость многочлена f(x) ÎP[x] зависит от поля, над которым он рассматривается, и есть в этом смысле понятие относительное.

Пример: Многочлен x^2 +1 над полем R неприводим, но над полем C он приводим.

Действительно: x^2+1=(x-i)(x+i), т.е. приводим надC.

Простейшие свойства неприводимых многочленов:

1) Всякий многочлен первой степени неприводим (это следует из определения)

f(x)=f1(x)f2(x), deg f(x)=1 Þ deg f1(x)=0 или 1, deg f2(x)=1 или 0;

2) Если f(x) неприводим над полем Р,то аf(x), где aÎP, a ≠ 0, тоже неприводим над полем Р;

3) Если f(x) неприводим над полем Ри g(x) ÎP[x] — некоторый многочлен над P , то ( f(x), g(x) )=1 либо f(x) │ g(x).

< Рассмотрим НОД многочленов (f(x), g(x))=d(x).Значит d(x) │ g(x) и d(x) │ f(x) Þ d(x) равен 1, т.е. (f(x), g(x))=1

или 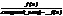, т.е. f(x) / g(x). >

4) Если произведение многочленов f(x)g(x) делится на неприводимый многочлен h(x) , то хотя бы один из множителей f(x) или g(x) делится на h(x) < Пусть h(x) ∤ f(x) Þпо свойству 3 (h(x),f(x))=1 Þ

Þ 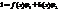и 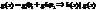, ибо h(x) │ f(x)g(x) и h(x) │ g(x)h(x). >

Теорема 1 (о разложении многочлена на неприводимые множители). Всякий многочлен f(x)ÎP[x] степени ≥1 можно представить в виде

произведения неприводимых над P многочленов. Разложение многочлена на неприводимые множители определено однозначно с точностью до многочлена нулевой степени и порядка следования сомножителей, то есть

если имеется два разложения f(x) на неприводимые множители:

f(x)= φ1(x)… φ S(x) = ψ1(x)… ψ k(x) , то s=k и при подходящей нумерации множителей : ψi =ai φi i = 1,…,s 0 ≠aiÎP.

< Сначала докажем существование:

Если f(x) — неприводим, то в разложении будет один множитель (всё ясно).

Если f(x) приводим, то он представляется в виде f(x) = f1(x)f 2(x). Если f1(x) и f 2(x) — неприводимые, то существование есть.

Если f1(x) или f 2(x) приводим, то с ним поступаем аналогично, как с f(x) и получаем дальше разложение f(x). Этот процесс на каком-то месте оборвётся, так как степени многочленов, которые мы получаем, всё время убывают. Это и доказывает первую часть теоремы.

Докажем вторую часть теоремы — однозначность.

Доказательство будем проводить индукцией по степени f(x). Если степень f(x) равна 1, то всё сводится к свойству 1.Утверждение считаем верным, если степень f(x) < n.Если f(x) неприводим, то доказывать нечего.

Если f(x) приводим, то возьмём разложение:

f(x)= φ1(x)… φ S(x) = ψ1(x)… ψ k(x).

Очевидно, что φ₁ делит произведение

φ1 | ψ1(x)… ψ k(x).

Следовательно, по свойству 4 φ1 | ψi Þ по свойству 2 ψi = aφ1.

После, может быть, перенумерации ψ_i можно считать ψ1 и Ψ1 =a1φ1.

φ1(x)… φ S(x) = ψ1(x)… ψ k(x)

Сократим обе части равенства на φ1. Получим

φ 2(x)… φ S(x) = ψ2(x)… ψ k(x) (1)

Обе части равенства (1) представляет собой многочлен степени меньше n. А для многочленов степени меньше n мы имеем индуктивное предположение, из которого следует, что s-1 = k-1 и Ψi =aiφi i=2, …,k после, может быть, перенумерации. >

Замечание1. Мы добьемся полной однозначности в каноническом смысле, если в разложении многочлена на неприводимые множители из каждого сомножителя вынесем его старший коэффициент:

f(x) = a p₁(x)… p _k(x) ; а – ст. к. f(x). ст. к. p_i = 1 (2)

Определение. Если неприводимый многочлен p(x) встречается в разложении (2) несколько раз, то он называется кратным множителем.

Например: если он встречается s раз, то он s-кратным. После этого разложение (2) допускает запись вида (3):

f(x) = a pk1 (x)… p km (x) ; p_i ≠ p_j (3)

Разложение (3) называют каноническим разложением многочлена на неприводимые. Оно определено однозначно (с точностью до порядка сомножителей).

Замечание 2. Задача о разложении многочлена на неприводимые над произвольным полем до сих пор не решена. Во многих случаях она решена. Мы приведем решение в случаях P=R;С.

Пусть f(x) =р^k(x)f1(x), где неприводимый многочлен р(x) не делит f1(x).

Тогда р(x) называют неприводимым множителем кратности к для многочлена f(x)

Теорема 2.Пусть р(x) — к-кратный неприводимый множитель для многочлена f(x). Тогда он является k-1-кратным неприводимым множителем для его производной.

Доказательство. Возьмем производную f(x):

f^’(x)=k p(^k-1)(x) p^'(x)f₁(x)+p(x)^k f₁^'(x) = p(^k-1)(x) (k p^'(x) f₁(x)+ p(x) f₁(x)).

Очевидно, что многочлен в скобках не делится на p(x), что и доказывает теорему.

КОРНИ МНОГОЧЛЕНА.

Пусть f(x) — некоторый многочлен над фиксированным полем P. f(x)=an x^n+…+a0ÎP[x]. И пусть c — некоторое число (не обязательно из P). Если мы подставим вместо x число c, то получим f(c) = an c^n+…+a0 — значение многочлена при x = c. Если f(x)=g(x), то f(c)=g(c).

Определение 1.Если f(c)=0, то с называют корнеммногочлена f(x) или корнем уравнения f(х)=0.

Разделим с остатком f(x) на (x-c): f(x)=(x-c)q(x)+r(x), где r(x)=0 и r(x)=aÎ, a¹0, то есть r(x) в любом случае число.

Следующая теорема позволяет найти остаток от деления f(x) на многочлен (x-a) не выполняя самого деления.

Теорема (Безу). Остаток от деления многочлена f(x) на многочлен (x-a) равен значению этого многочлена при x=a.

Следствие. а является корнем f(x) тогда и только тогда,когда (x-а) делит f(x).

< Þ f(a)=0 (т.к. а-корень). Значит по теореме Безу (x-a) делит

f(x) Ü f(x)=(x-a)f1(x). Очевидно f(a)=0. >

Это позволяет свести нахождение всех корней многочлена к нахождению делителя первой степени. Это можно сделать при помощи схемы Горнера.

Схема Горнера:

Пусть f(x)= a0 x^n +…+an. Разделим многочлен f(x) на x-a:

f(x)=(x-a ) f 1(x)+r (1)

где

f₁ (x)=b0 x(^n-1)+…+(b) (n-1).

Сравним коэффициенты при одинаковых степенях в равенстве (1):

x^n : a0=b0

x(^n-1) : a1=b1-a b0

x(^n-2) : a2=b2-a b1

…

x^0: an = r -a (b)(n-1).

Отсюда имеем:

b0=a0

b1=a1 + a b0

b2=a2+ a b1 (2)

… …

r= an +a (b)(n-1).

Для запоминания вычисления коэффициентов применяют схему Горнера. Делают таблицу следующего вида:

	a0 a1 a2 … an
a	a0 a1+b0 c …

В первой строке этой таблицы выписывают один за другим все коэффициенты f(x), а во второе слева — элемент a. Коэффициенты частного f1(x) и остаток записывают последовательно во второй строке, согласно равенствам (2).

29 – 30.