Вопрос 3.2. Разложение многочлена на множители

Теорема 3.3. (Основная теорема алгебры). Любой многочлен n-й степени имеет хотя бы один комплексный корень.

Теорема приводится без доказательства.

Замечание 3.1. Вещественных корней многочлен может не иметь.

Теорема 3.4. (теорема Безу). Остаток от деления многочлена 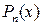на двучлен 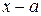равен значению многочлена в точке a

.

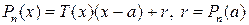Доказательство. Пусть a корень многочлена 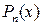, тогда разделив его на линейный многочлен 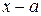, получим

,

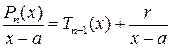где r – остаток от деления, представляющий собой число.

Тогда 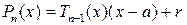, и, следовательно, .

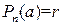Конец доказательства.

Следствие 3.1. Если a корень многочлена 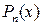, то он делится без остатка на 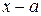, т.e.

.

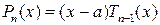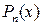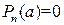Доказательство. Если a корень многочлена , то и тогда r=0.

Конец доказательства.

Следствие 3.2. Если a корень многочлена 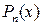, то его можно представить в виде 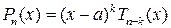, где k натуральное число и 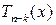многочлен неравный 0 при .

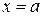Доказательство. Согласно следствию 3.1 из теоремы Безу 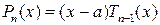. Если a есть корень многочлена 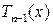, то, применяя следствие 3.1, получим

.

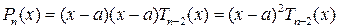Продолжая этот процесс, получим многочлен 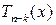, корнем которого число a не является: .

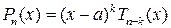Конец доказательства.

Теорема 3.4. Если 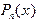‑ многочлен n-й степени с действительными коэффициентами имеет комплексный корень a, то комплексно сопряженное к нему число 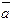то же является корнем того же многочлена.

Доказательство. Подставим корень a в уравнение 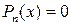и выполним комплексное сопряжение

,

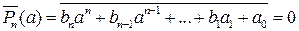тогда получим

.

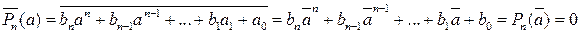Конец доказательства.

Пример 3.3. Многочлен 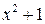имеет корни .

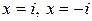Конец примера.

Следствие 3.3. Если b комплексный корень многочлена 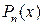, то его можно представить в виде

,

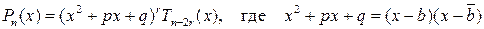причем p и q - вещественные числа, r - натуральное число, такое что 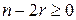, 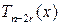‑ многочлен, не равный 0 при .

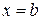Доказательство. Пусть b комплексный корень, тогда согласно следствию 3.1 можно записать

.

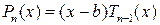Комплексно сопряженное число 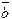будет корнем многочлена 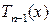. Тогда применяя к нему следствие 3.1, получим

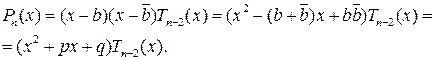
Продолжая этот процесс, получим многочлен 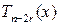, корнем которого число b не является .

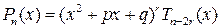Конец доказательства.

Теорема 3.6. Любой многочлен n-й степени можно разложить на множители вида 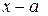и 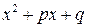с действительными коэффициентами:

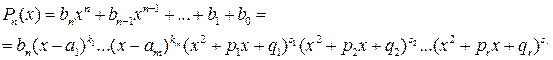
где числа k и s ‑ кратности соответствующих вещественных и мнимых корней, причем .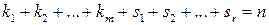

Доказательство. Согласно основной теоремы алгебры любой многочлен 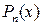имеет хотя бы один корень. Пусть это 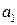. Тогда из следствия 3.3 следует, что

.

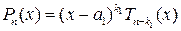Продолжая эти рассуждения уже для многочлена 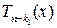, мы можем прийти через конечное число шагов к формуле

,

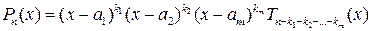где многочлен 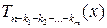не имеет действительных корней. Тогда должен существовать комплексный корень 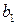и комплексно сопряженный к нему корень 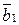. Из следствия 3.3 получим

.

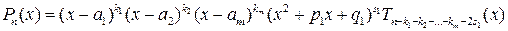Продолжая эти рассуждения, мы получим через конечное число шагов разложение

.

Многочлен 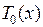не имеет корней и, следовательно, является константой. Значение ее легко найти, если сообразить, что она равна коэффициенту при старшей степени x. Отсюда получаем, что .

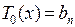Конец доказательства.

Пример 3.4. Разложить многочлен 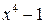на множители с вещественными коэффициентами

.

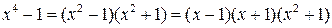Он имеет корни .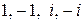

Конец примера.